1.简述

      

本文将涉及到数理统计的最后一个模块——参数估计，后续将更新的模块是多项式计算、数据插值和曲线拟合。
在讲述使用matlab来实现参数估计之前，有必要去了解一些基本原理。
1.离散型随机变量的极大似然估计法:
(1) 似然函数
若X为离散型, 似然函数为

(2) 求似然函数L(θ)的最大值点 θ, 则θ就是未知参数的极大似然估计值.
2.连续型随机变量的极大似然估计法:
(1) 似然函数
若 X 为连续型, 似然函数为

(2) 求似然函数L(θ)的最大值点θ, 则θ就是未知参数 的极大似然估计值.
一、矩估计
设总体X的均值、方差均存在，样本（X1，X2，……，X n）,则不管总体服从什么分布，总体均值的矩估计均为样本均值，方差的矩估计均为样本二阶中心矩。
matlab中提供了下列函数来实现总体均值的矩估计值与方差的矩估计值的计算，如下：
mu_ju=mean(X) % 返回样本X的均值
sigma2_ju =moment(X,2) % 返回样本X的2阶中心矩
 

二、单个总体极大似然估计与区间估计（参数均未知）
命令: [a,b]=namefit (X, ALPHA) % 返回总体参数的极大似然估计a与置信度为100(1- ALPHA)的置信区间 [a,b]，若参数为多个，ab也是多个，若省略ALPHA，则置信度为0.95
下表列出了几种常用分布的参数估计函数：

函数名    调 用 形 式    函 数 说 明
binofit    PHAT= binofit(X, N)；[PHAT, PCI] = binofit(X,N)；[PHAT, PCI]= binofit (X, N, ALPHA)    二项分布的概率的最大似然估计置信度为95%的最大似然估计和置信区间返回水平α的参数估计和置信区间
poissfit    Lambdahat=poissfit(X)；[Lambdahat, Lambdaci] = poissfit(X)；[Lambdahat, Lambdaci]= poissfit (X, ALPHA)    泊松分布的参数的最大似然估计置信度为95%的最大似然估计和置信区间返回水平α的λ参数和置信区间
normfit    [muhat,sigmahat,muci,sigmaci] = normfit(X)；[muhat,sigmahat,muci,sigmaci] = normfit(X, ALPHA)    正态分布的最大似然估计，置信度为95%返回水平α的期望、方差值和置信区间
betafit    PHAT =betafit (X)；[PHAT, PCI]= betafit (X, ALPHA)    返回β分布参数a和 b的最大似然估计返回最大似然估计值和水平α的置信区间
unifit    [ahat,bhat] = unifit(X)；[ahat,bhat,ACI,BCI] = unifit(X)；[ahat,bhat,ACI,BCI]=unifit(X, ALPHA)    均匀分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计和置信区间
expfit    muhat =expfit(X)；[muhat,muci] = expfit(X)；[muhat,muci] = expfit(X,alpha)    指数分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计和置信区间
gamfit    phat =gamfit(X)；[phat,pci] = gamfit(X)；[phat,pci] = gamfit(X,alpha)    γ分布参数的最大似然估计置信度为95%的参数估计和置信区间返回最大似然估计值和水平α的置信区间
weibfit    phat = weibfit(X)；[phat,pci] = weibfit(X)；[phat,pci] = weibfit(X,alpha)    韦伯分布参数的最大似然估计置信度为95%的参数估计和置信区间返回水平α的参数估计及其区间估计
Mle    phat = mle(‘dist’,data)；[phat,pci] = mle(‘dist’,data)；[phat,pci] = mle(‘dist’,data,alpha)；[phat,pci] = mle(‘dist’,data,alpha,p1)    分布函数名为dist的最大似然估计置信度为95%的参数估计和置信区间返回水平α的最大似然估计值和置信区间仅用于二项分布，pl为试验总次数

 

2.代码及运行结果

%%  区间参数估计   均匀分布
clear all;
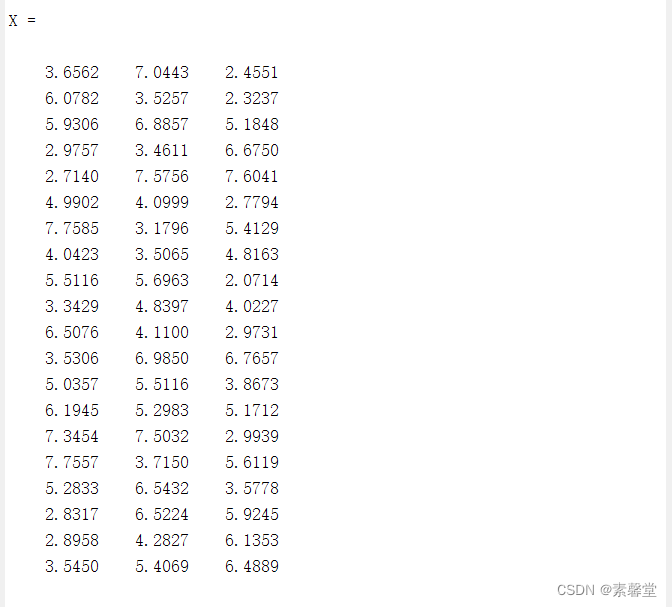
X=unifrnd(2,8,20,3)
[a,b,aci,bci]=unifit(X,0.05)

 

 

 

%%   指数分布的参数估计
clear all;
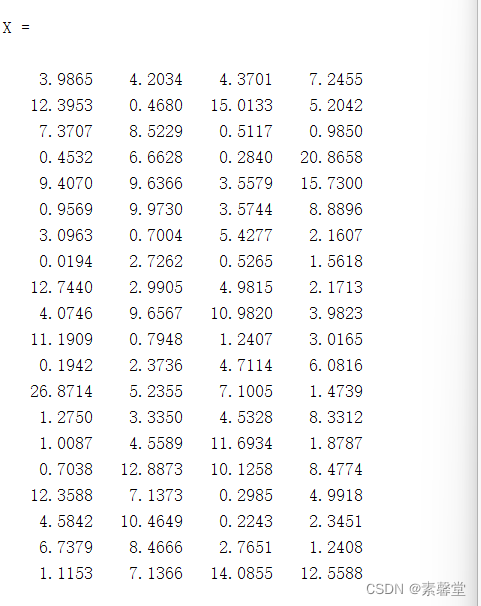
X=exprnd(5,20,4)
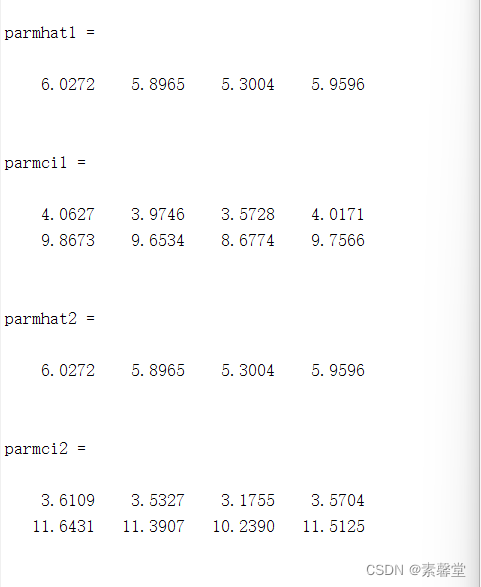
[parmhat1,parmci1]=expfit(X,0.05)     %置信度95%
[parmhat2,parmci2]=expfit(X,0.01)

 

 

 

%%  beta分布的参数估计
% 
clear all;
X=betarnd(7,5,100,1);
[phat,pci]=betafit(X,0.02)

 

 

%%  正态分布的参数估计
% 
clear all;
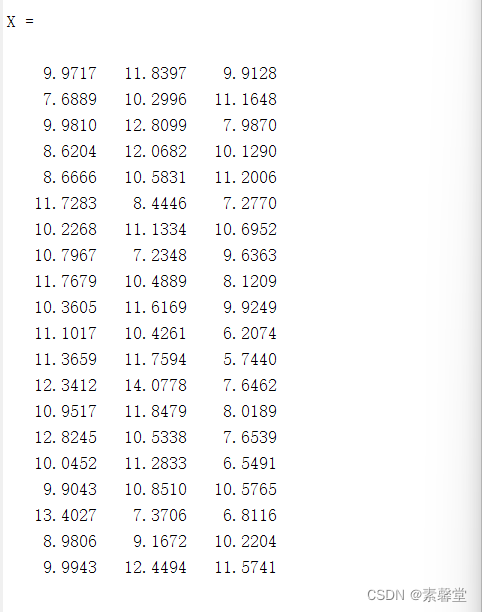
X=normrnd(10,2,20,3)
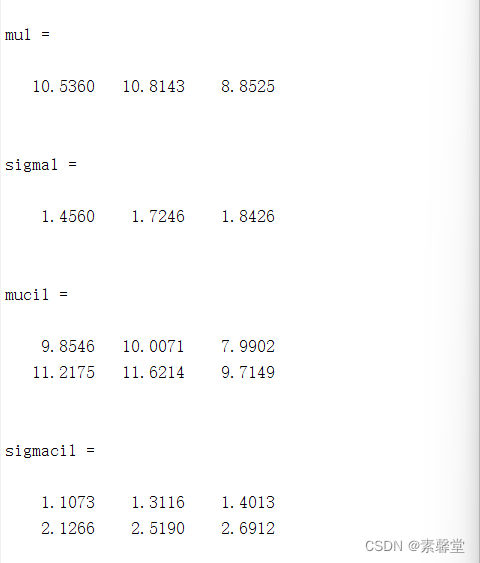
[mu1,sigma1,muci1,sigmaci1]=normfit(X,0.05)
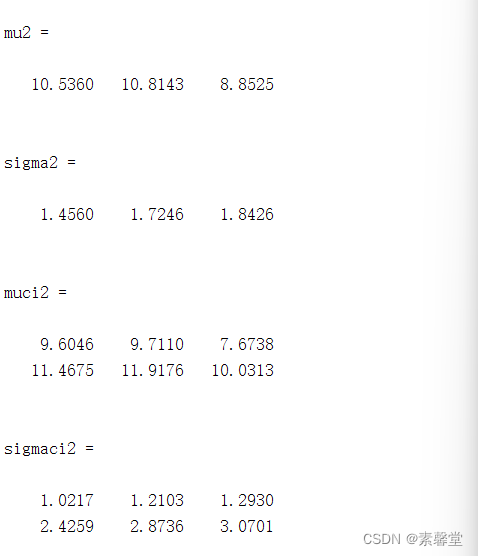
[mu2,sigma2,muci2,sigmaci2]=normfit(X,0.01)