【机器学习】十大算法之一 “PCA”-编程知识

作者主页：爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域.https://blog.csdn.net/Code_and516?type=blog个人简介：打工人。

持续分享：机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。

如发现文章有误，麻烦请指出，我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com

PCA算法是机器学习中最重要的十大算法之一，它是一种数据维度压缩和特征选择的方法。

本文将详细讲解机器学习十大算法之一“PCA”

一、PCA算法简介

二、PCA的发展历史

三、PCA算法公式与讲解

1. 主成分分析：

（1）归一化数据

（2）计算协方差矩阵

（3）计算特征值和特征向量

（4）计算主成分

2. 数据投影和重建

四、PCA算法原理

五、PCA算法功能

1. 降维

2. 压缩

3. 特征提取

4. 去噪

六、PCA算法示例代码

七、总结

一、PCA算法简介

PCA（Principal Component Analysis，主成分分析）是一种广泛使用的线性降维算法，在机器学习领域被广泛应用。通俗地说，它是一种通过将高维数据映射到低维数据，保留数据主要特征的方法。在PCA中，数据被投影到一个新的低维抽象空间中，使新的特征集能最大化地解释数据集的方差，我们可以选择保留最大方差的前k个特征值。通常，PCA被用于降维，但它也被用作一种特征提取算法。

二、PCA的发展历史

PCA算法最早由卡尔·皮尔逊（Karl Pearson）于1901年提出。他最初将PCA作为一种数据分析工具来解决数据相关性问题，PCA的目标是找到最小维度的线性空间，该空间能够最准确地描述数据集的统计特征。在20世纪50年代，P. C. Mahalanobis提出了第一个数学实现PCA算法的方法。随后，PCA被广泛应用于信号处理、图像处理、语音识别和数据挖掘等领域。在现代机器学习中，PCA通常是第一个选项，用于处理大量高维数据集的降维。

三、PCA算法公式与讲解

PCA算法主要由两部分组成：主成分分析和数据投影。

下面是PCA算法的数学公式和讲解：

1. 主成分分析：

设X是一个n个观察值和p个变量的数据矩阵（n > p），其中每一行表示一个观察值，每列表示一个变量，计算过程如下：

（1）归一化数据

其中，xˉi表示第i个特征值的均值。

（2）计算协方差矩阵

其中，σij表示第i个特征值和第j个特征值之间的协方差。

（3）计算特征值和特征向量

对于协方差矩阵Σ，我们可以求解它的特征值和特征向量。其中，特征向量v满足：

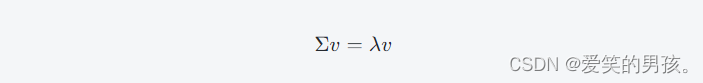
其中，λ是特征向量v对应的特征值。特征值和特征向量的计算通常使用标准矩阵计算库（如NumPy）进行。

（4）计算主成分

对于数据矩阵X，我们可以通过计算它的主成分来实现降维。PCA的目标是找到主成分，这些主成分能够最大化数据集的方差。对于特征向量v和对应的特征值λ，计算它们的PCA成分为：

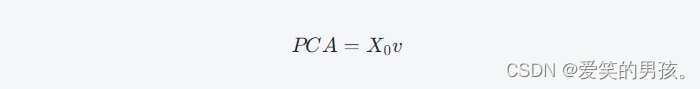
这些PCA成分包含了原始数据矩阵X的大部分信息。PCA的前k个成分可以用于数据的降维表示。

2. 数据投影和重建

PCA还可以对原始数据进行投影和重建。给定一个新的观察值x，可以通过计算其PCA投影来实现数据的降维：

其中，vk是前k个主成分的向量。原始数据可以通过反向投影进行重建：

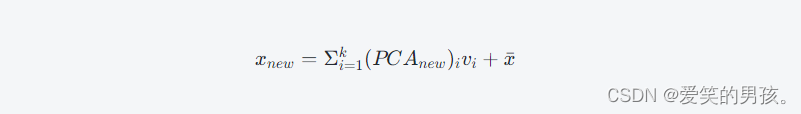
其中，xˉ是原始数据的均值。这个过程可以通过计算反向PCA投影来实现。

四、PCA算法原理

PCA算法的原理是将高维数据集映射到低维空间中，同时保留数据集的主要信息。具体来说，PCA通过计算协方差矩阵和特征向量来确定数据集的主方向，然后将数据集投影到主方向上。在新的低维空间中，每个特征值都是线性无关的，并且是数据变化的主要方向，因此，它们可以更好地表示数据集。

五、PCA算法功能

PCA算法在机器学习中有许多用途，如：

1. 降维

PCA可以将高维数据集降到更低的维度，减少数据存储和处理的开销。

2. 压缩

PCA可以将数据集表示为比原始数据集更紧凑的形式，可以用于数据压缩。

3. 特征提取

PCA可以从原始数据集中提取最重要的特征，这些特征可以用于构建更好的模型。

4. 去噪

PCA可以帮助我们去除噪声，并且使数据集更具可分性。

六、PCA算法示例代码

下面是Python中实现PCA算法的示例代码：

# -*- coding: utf-8 -*-
import numpy as np
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt# 加载Iris数据集
data = load_iris()
X = data.data
y = data.target
target_names = data.target_names# 将数据集降维到两个成分
pca = PCA(n_components=2)
X_r = pca.fit_transform(X)# 绘制降维后数据的散点图
colors = ['navy', 'turquoise', 'darkorange']
lw = 2
for color, i, target_name in zip(colors, [0, 1, 2], target_names):plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw, label=target_name)
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA of IRIS dataset')
plt.show()

上述代码中，我们首先加载sklearn中的Iris数据集，然后使用PCA算法将其降维到两个成分。最后，我们绘制了降维后的数据集的散点图。

运行结果如下：

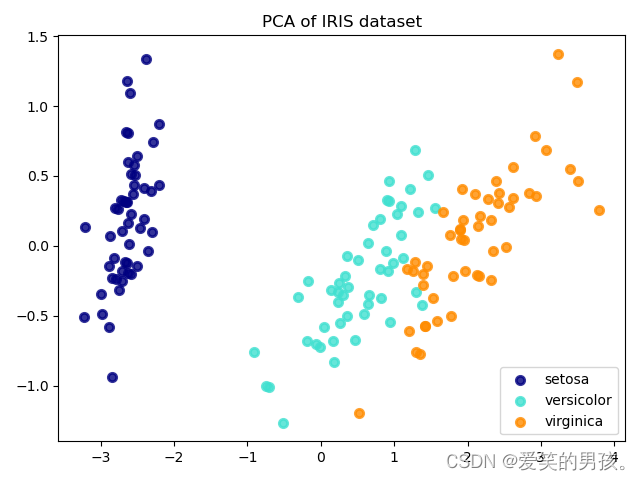
可以看到，使用PCA算法，我们将原始数据集降到了两个成分。散点图显示数据集的三个不同类别在新的低维空间可以更清晰地分离开。

七、总结

在本文中，我们介绍了PCA算法的基本原理，讨论了它的应用，以及在Python中如何实现。PCA算法是一种广泛使用的算法，用于降维、特征提取和数据压缩等。它可以使数据集更易于处理，并提供更好的可视化效果。但是，PCA也有一些限制，例如不能更好地理解非线性数据集。在实践中，PCA通常与其他算法一起使用，以获得更好的结果。