目录
1 什么是MDP-Based Planning
2 worst-case analysis for nondeterministic model
3 Expected Cost Planning
4 Real Time Dynamic Programming(RTDP)
1 什么是MDP-Based Planning
之前我们从起点到终点存在很多可执行路径,我们可以通过执行的时候根据环境的变化去选择最优的路径。
到目前为止,我们假设机器人是在理想情况下进行的planning(机器人的执行是完美的、机器人的估计是完美的)。
用上面两幅图说,我们规划一个地点到另一个地点的路线,我们假设让机器人走一个格子它就走一个格子。右图的话我们假设精准的反映环境的情况,估计好位姿以后,假设机器人精准的到了终点的位姿不存在意外情况。
实际并非如此:
当在实际应用中,执行和状态估计都不是完美的。
• 执行不确定性:打滑、崎岖地形、风、空气阻力、控制误差等。
• 状态估计不确定性:传感器噪声、校准误差、不完美估计、部分可观测性等。
不确定性可以从机器人的视角分为两类,这表明机器人可以利用多少信息。
不确定性模型
• 非确定性:机器人不知道会有什么类型的不确定性或干扰被添加到其行为(下一步动作)中。(偏移目标点非常远受自然环境影响)
• 概率性:机器人通过观察和收集统计数据对不确定性有一定估计。(运行一部分后直到自己受干扰程度)
为了正式描述这个概念,我们首先引入两个决策者来模拟不确定性的产生,然后是带有不确定性的规划类型。
决策者(游戏参与者):
• 机器人是主要的决策者,根据完全已知的状态和完美执行进行规划。
• 自然界向机器人制定的计划添加不确定性,这对机器人来说是不可预测的。
Formalization-7.1:与自然界的博弈(独立博弈)
• 非空集合 U 称为机器人行动空间(robot action space)。每个 u ∈ U 被称为机器人行动。
• 非空集合 Θ 称为自然界行动空间(nature action space)。每个 θ ∈ Θ 被称为自然界行动。
• 函数 L:U × Θ → R ∪ {∞},称为成本函数(cost function)或负奖励函数。Formalization-7.2:自然界了解机器人行动(依赖博弈)
• 非空集合 U 称为机器人行动空间。每个 u ∈ U 被称为机器人行动。
• 对于每个 u ∈ U,有一个非空集合 Θ(u) 称为自然界行动空间。
• 函数 L:U × Θ → R ∪ {∞},称为成本函数或负奖励函数。
在机器人与自然界进行博弈时,对机器人来说什么是最佳决策?一步最坏情况分析(One-step Worst-Case Analysis)
• 在非确定性(Nondeterministic)模型下,独立博弈中的 P(θ) 和依赖博弈中的 P(θ|u_k) 是未知的;
• 机器人无法预测自然界的行为,并假设它恶意地选择会使成本尽可能高的行动;
• 因此,假设最坏情况下做出决策是合理的。
我们穷举所有的nature action space,从中筛选出最不利的这种情况让机器人执行这个动作将最不利降到最低。
• 在概率模型下,独立博弈中的 P(θ) 和依赖博弈中的 P(θ|u_k) 是已知的;
• 假设已经观察到了应用的自然界行动,并且自然界在选择行动时采用了随机化策略。
• 因此,我们优化获得平均成本(average cost to be received)。
机器人每执行一个动作,环境会对齐施加各种影响,我们去求一下各种影响的期望选择让期望值最小的一个动作。
多步的情况下呢?
Formalization-7.2:带有自然界的离散规划
1. 具有初始状态 x_s 和目标集合 X_F ⊂ X 的非空状态空间 X。
2. 对于每个状态 x ∈ X,有一个有限且非空的机器人行动空间 U(x)。对于每个 x ∈ X 和 u ∈ U(x),有一个有限且非空的自然界行动空间 Θ(x, u)。
3.状态转移函数 f (x, u, θ) 对于每个 x ∈ X, u ∈ U,和 θ ∈ Θ(x, u):
4.一组阶段(机器人不由但一阶段表示),每个阶段用 k 表示,从 k = 1 开始并无限持续,或者在最大阶段 k = K + 1 = F 结束。
5.一个阶段叠加的成本函数 L。让 x̃ F,ũ k,θ̃ K 表示截止到第 K 阶段的状态历史、机器人行动和自然界行动:
马尔可夫决策过程(MDP)
在学习领域,MDP 是一个 4 元组 (S, A, P, R),在规划领域则是 (X, U, P, L):
• S 或 X 是状态空间,
• A 或 U 是(机器人)动作空间,
• P(x_k+1 |x_k, u_k) 是概率模型下的状态转移函数,在非确定性模型下退化为一个集合 X_k+1 (x_k, u_k),
• R(x_k, x_k+1) 是即时奖励,或者是由于 u、θ 从 x_k 过渡到 x_k+1 的负一步成本 −l(x_k, u_k, θ_k)。
面对不确定性进行规划的第一个难题在于用 MDP 模型适当地形式化我们的问题。
机器人从
移动到
,状态空间就是布满黑点的区域。动作空间就是五种(停留在原地、上下左右)。
nature的动作空间:
1.我们假定机器人在
这个位置执行了
动作含一个随机的高斯误差。(连续)
2.对nature的动作空间进行离散化的定义,机器人在
这个位置执行了
动作加上一个额外的动作。(离散)
代价函数l:下一个状态与当前状态的距离差。
我们希望找一个路径(以最小的代价移动到目标位置)。
是状态空间到动作空间的一个映射,它规定了在什么状态下我应该执行一个什么样的动作,是一个离散集合的形式。
定义衡量policy好坏的变量:
33
2 worst-case analysis for nondeterministic model
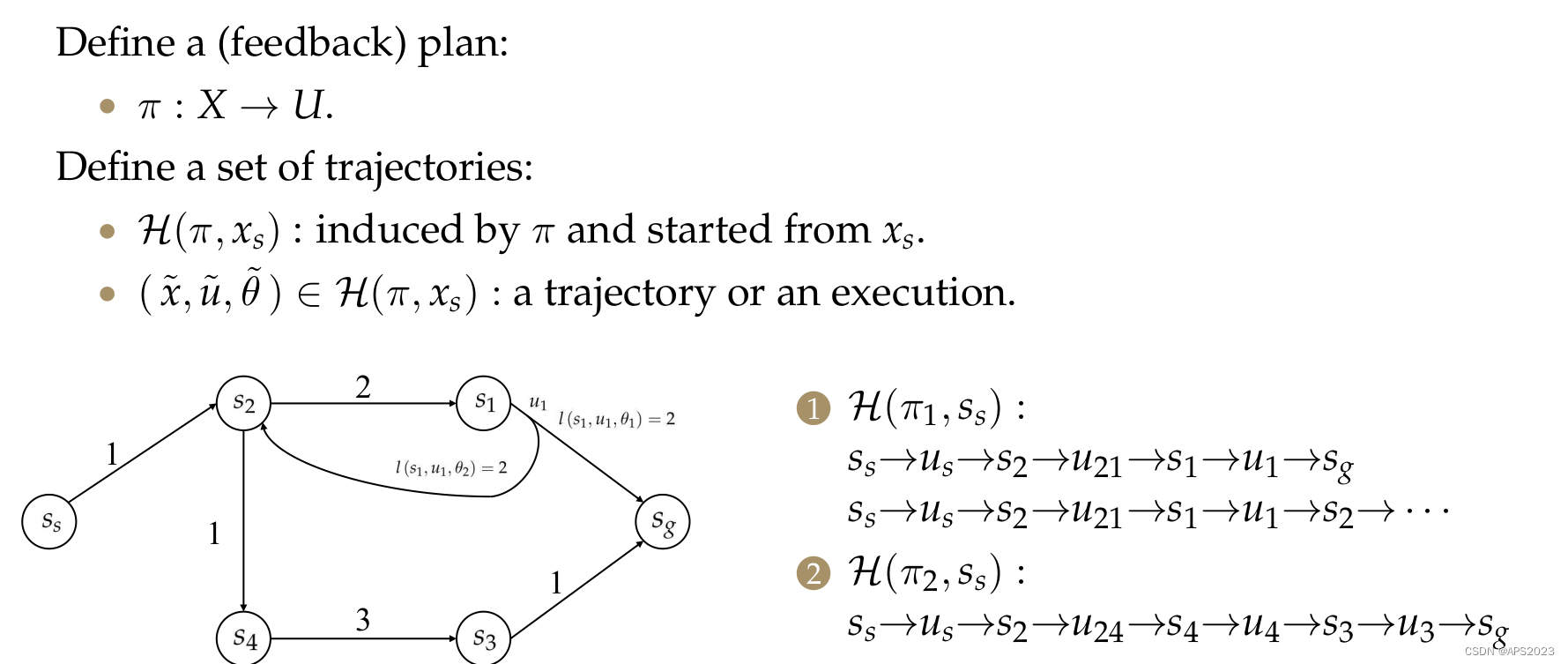
我们拿一个具体的例子:
第K+1步最优的cost to go已经知道了,我们现在在当前状态
机器人执行了特征的动作
,机器人能从这个
转移到具体的哪个
是由
决定的。我们找一个
使得单步的cost加上K+1的cost to go和最大的
,我们再去选择cost最小的
。
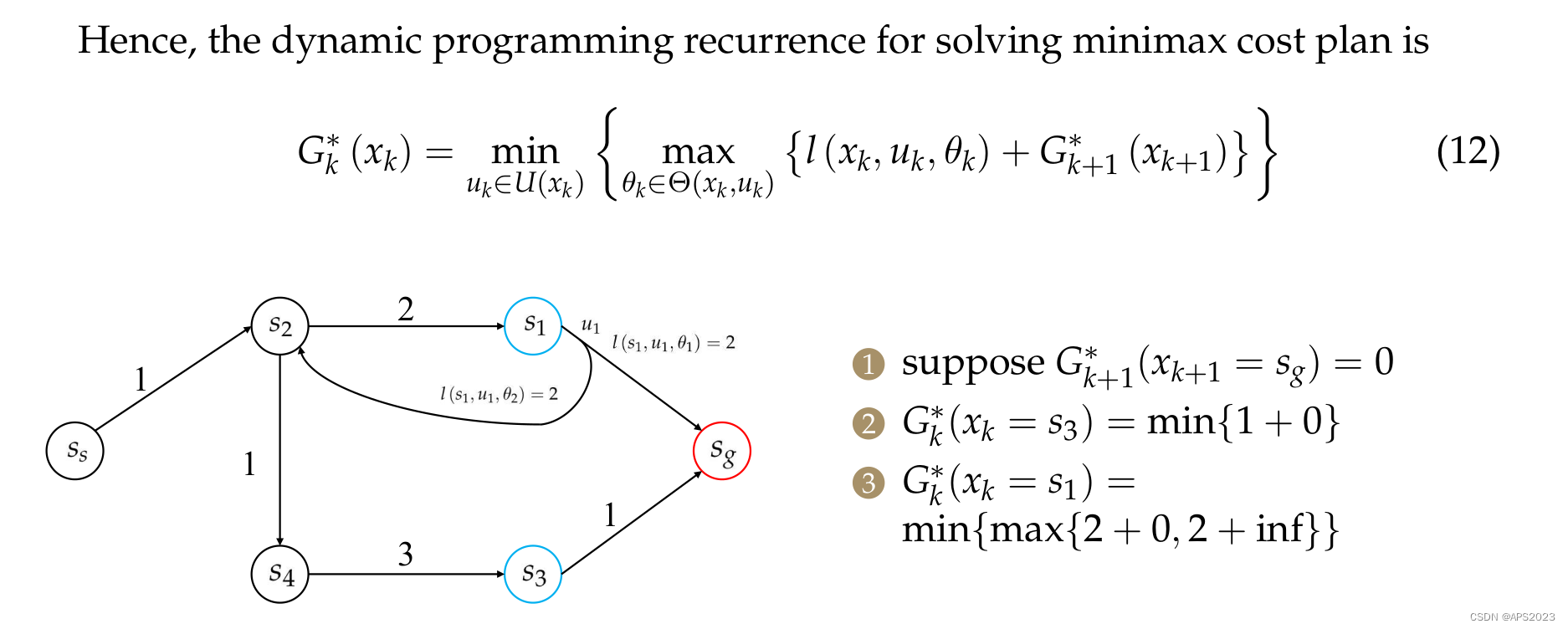
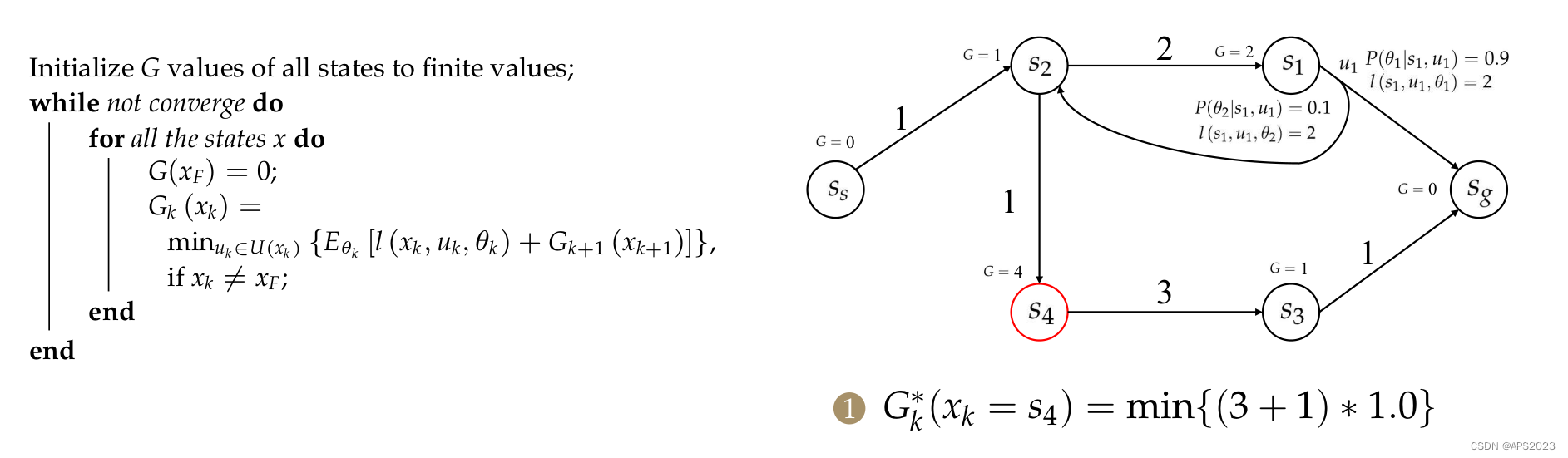
我们假设终点处的cost to go是0,其他地方未知。S3来说,cost to go为0+1。s1来说,只有一个u,但是有两个
,一个是单步2 + 终点0,另一个分支的话 2 + s2的cost to go(还未计算)。
从终点到起点迭代求解。
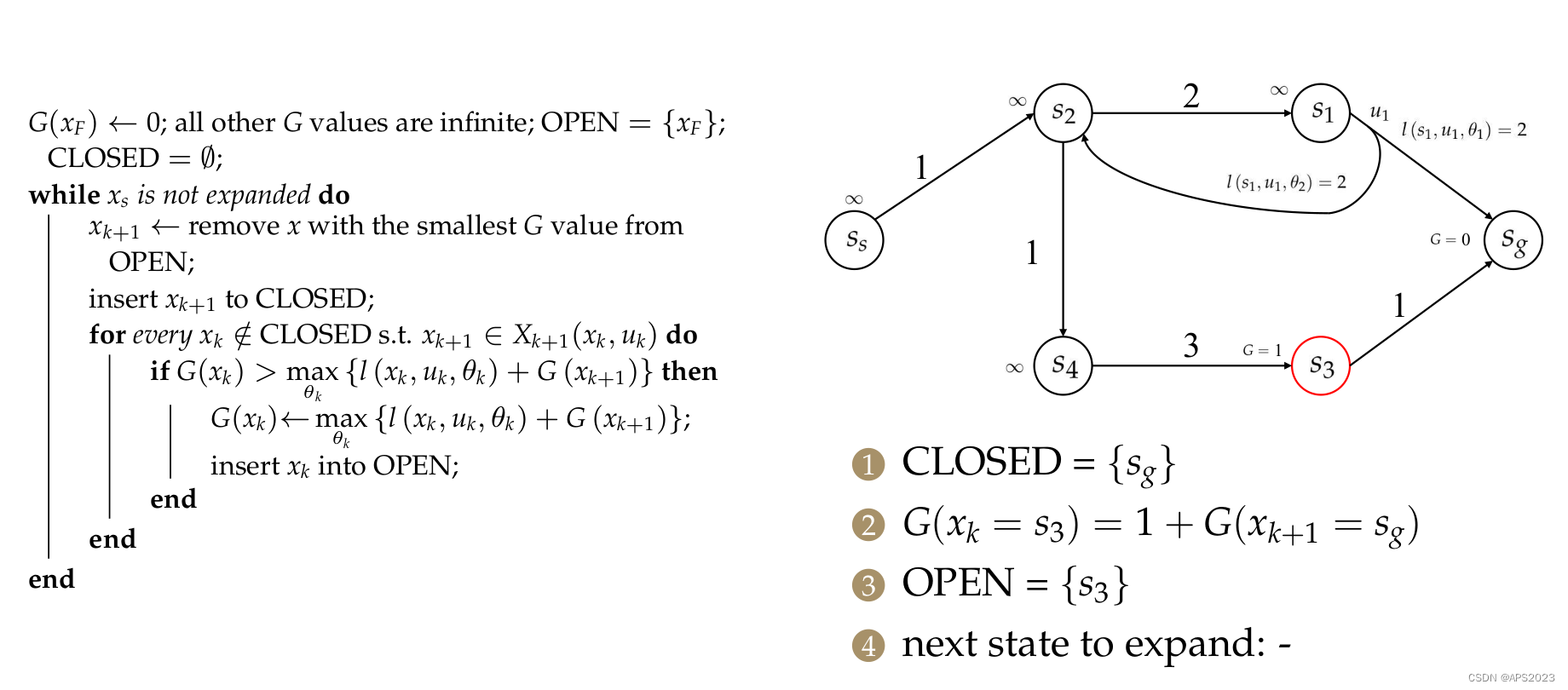
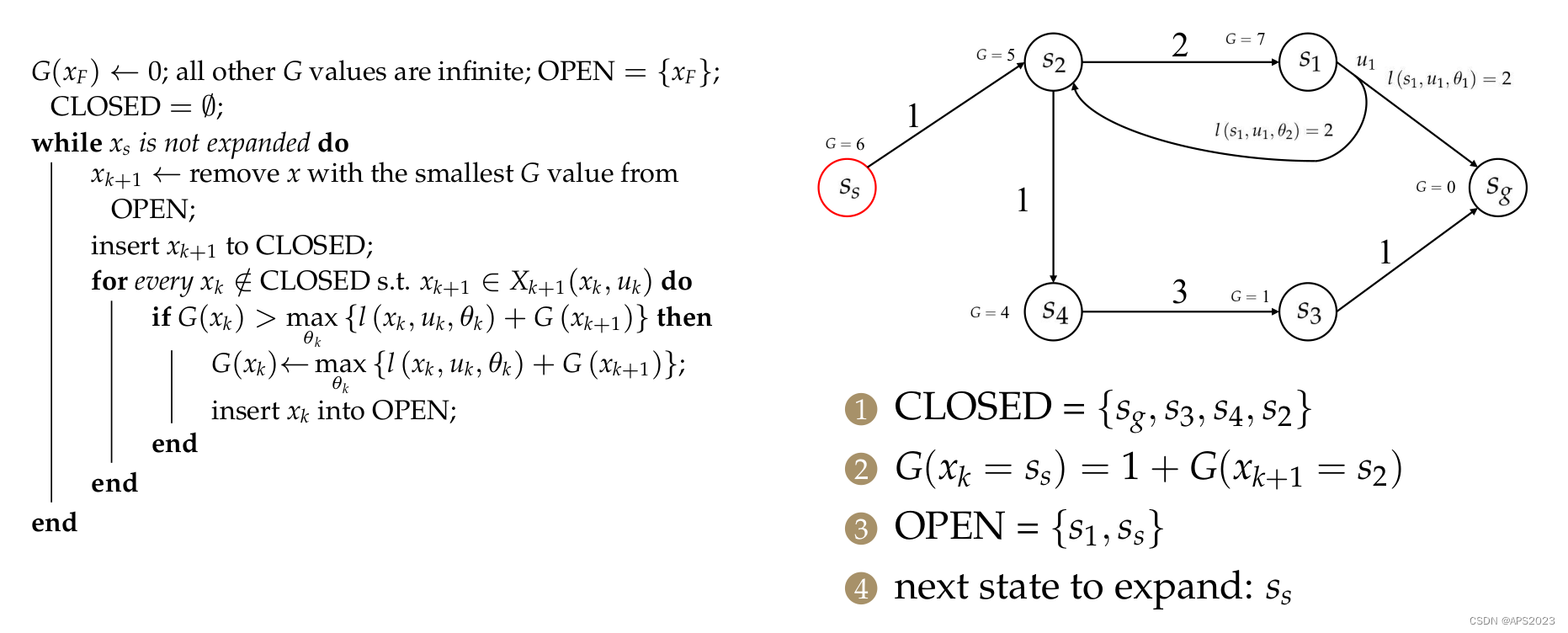
举一个例子:
首先我们将
,其他的设置为无穷,将openlist初始化为
。
下一次待扩展状态为
。下一步找其前继节点。
对于
,计算
,openlist添加
。
对于
,
(inf.....不能更新,无法放入openlist),
。
对于s4,相同的。
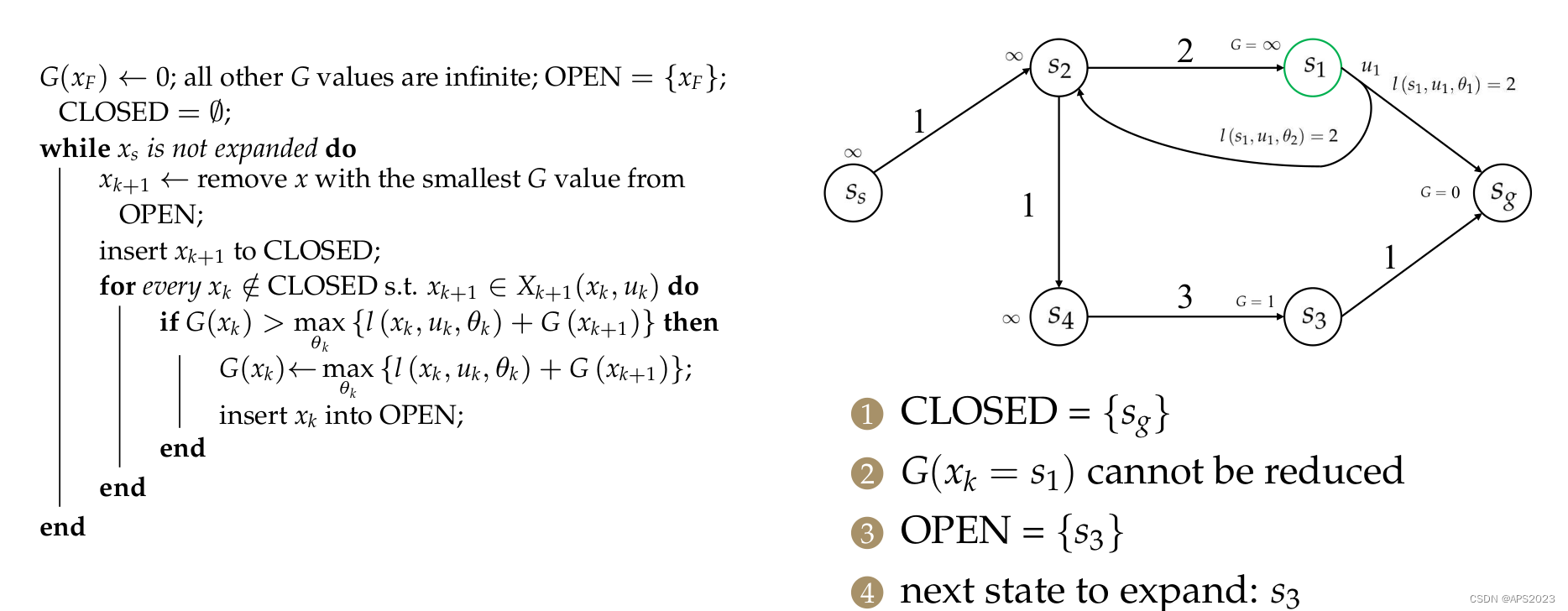
对于s2,也是相同的。不过它有两个前继节点
。先对S1进行处理:
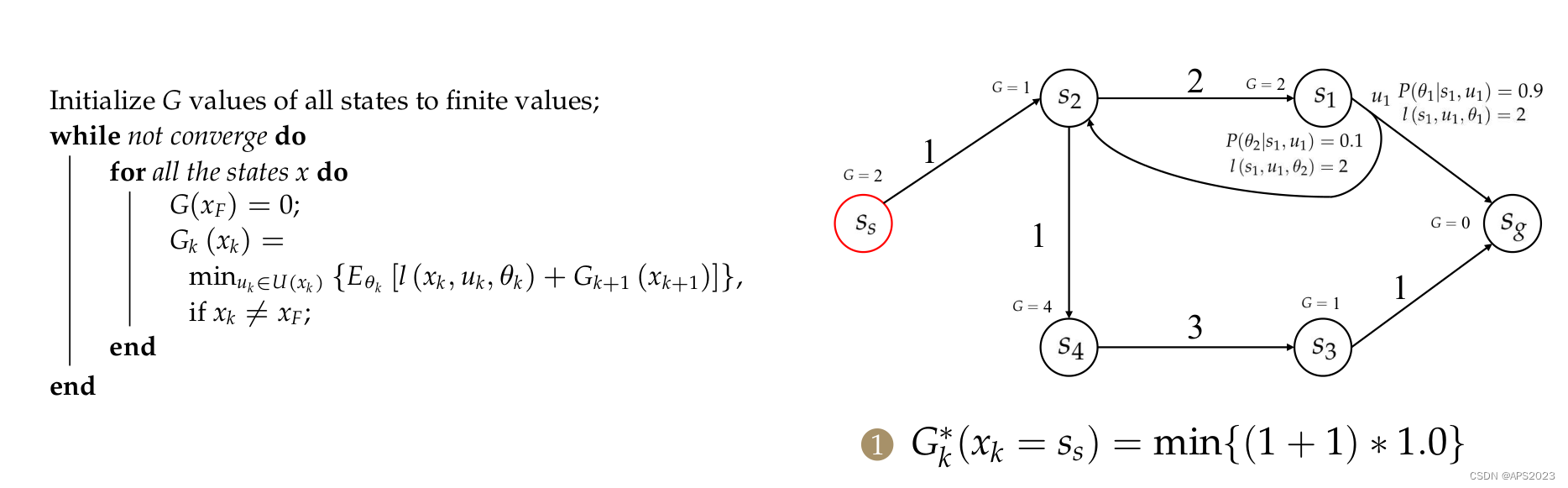
最后更新Ss:
优点、缺点:
3 Expected Cost Planning
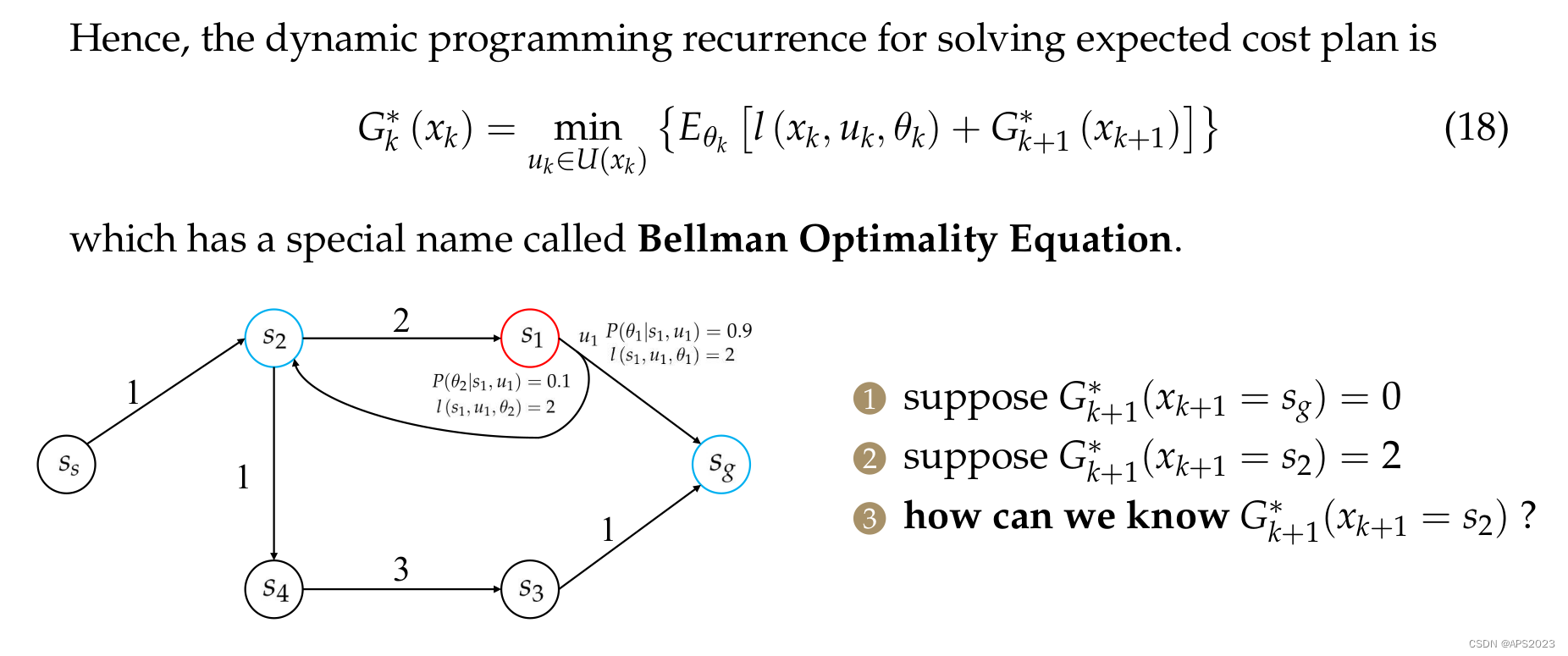
那么问题来了?
我们来看算法描述:
举个例子把:
首先我们把
初始化为0。选择一个迭代顺序
。
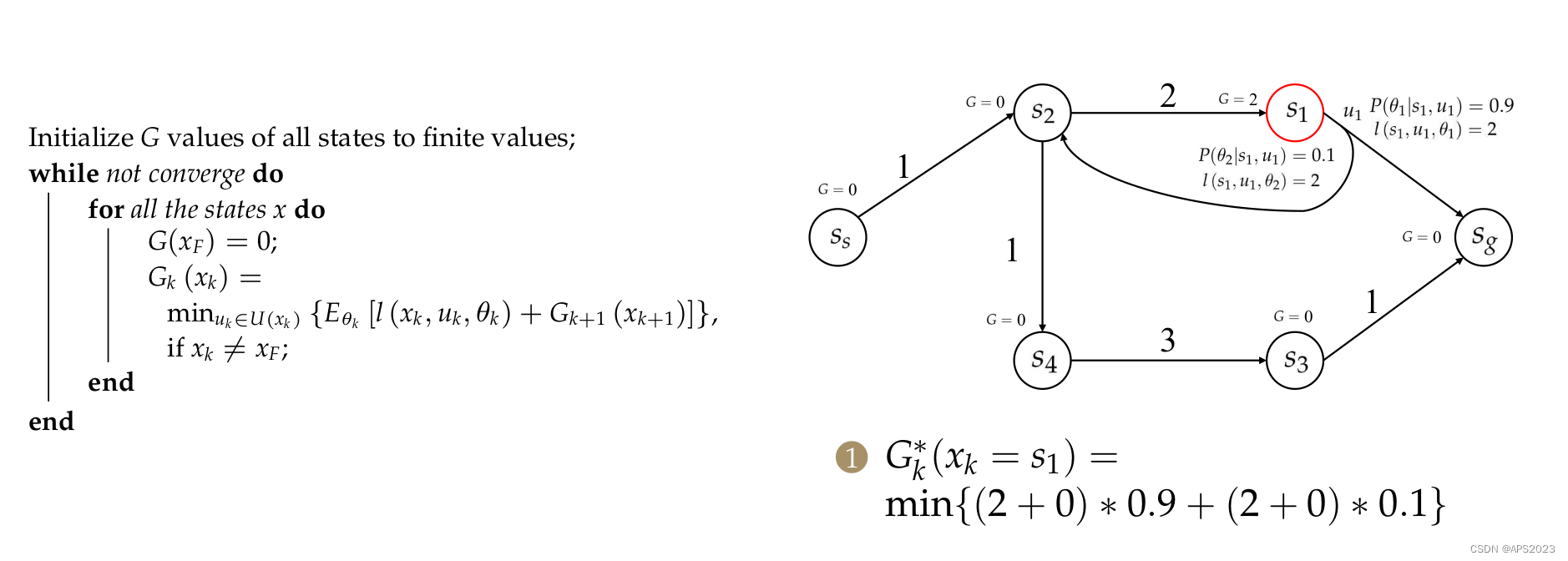
先来看
的更新:
在来看
的更新:
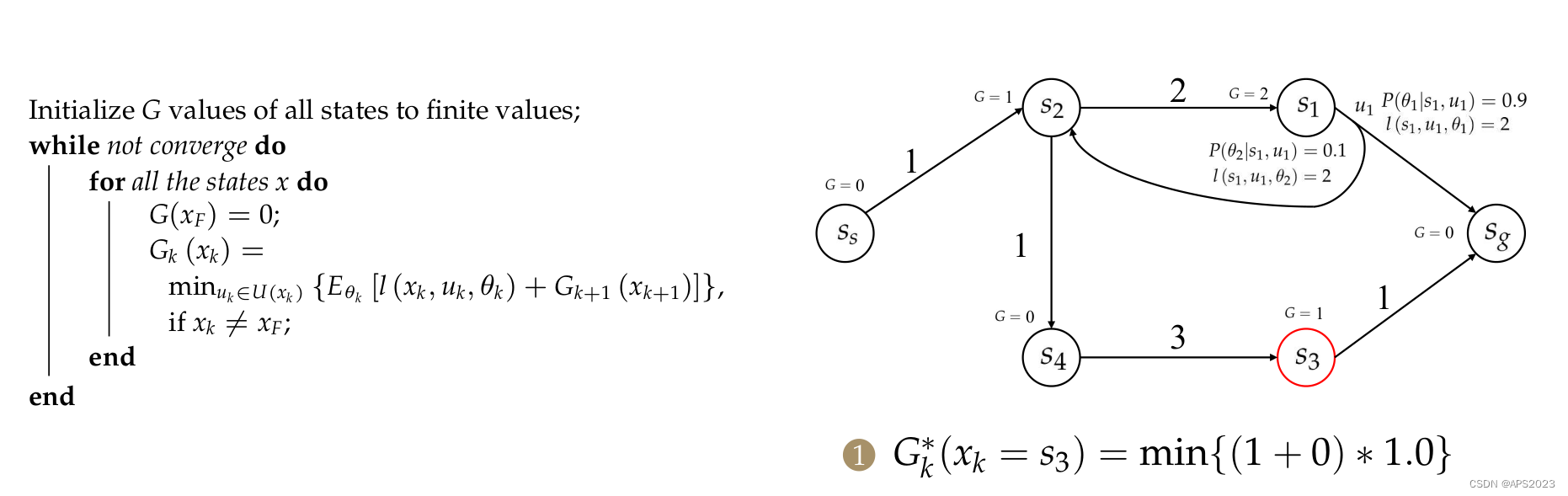
在来看
的更新:
在来看
的更新:
最后对
的更新:
经过一轮之后我们有了G。我们接着进行第二轮迭代:
。。。。第三次迭代
如何判断收敛?边界条件??如何改进??迭代次序怎么来改进??
优点&缺点:
1.反映的是平均的水平
2.不一定是最优
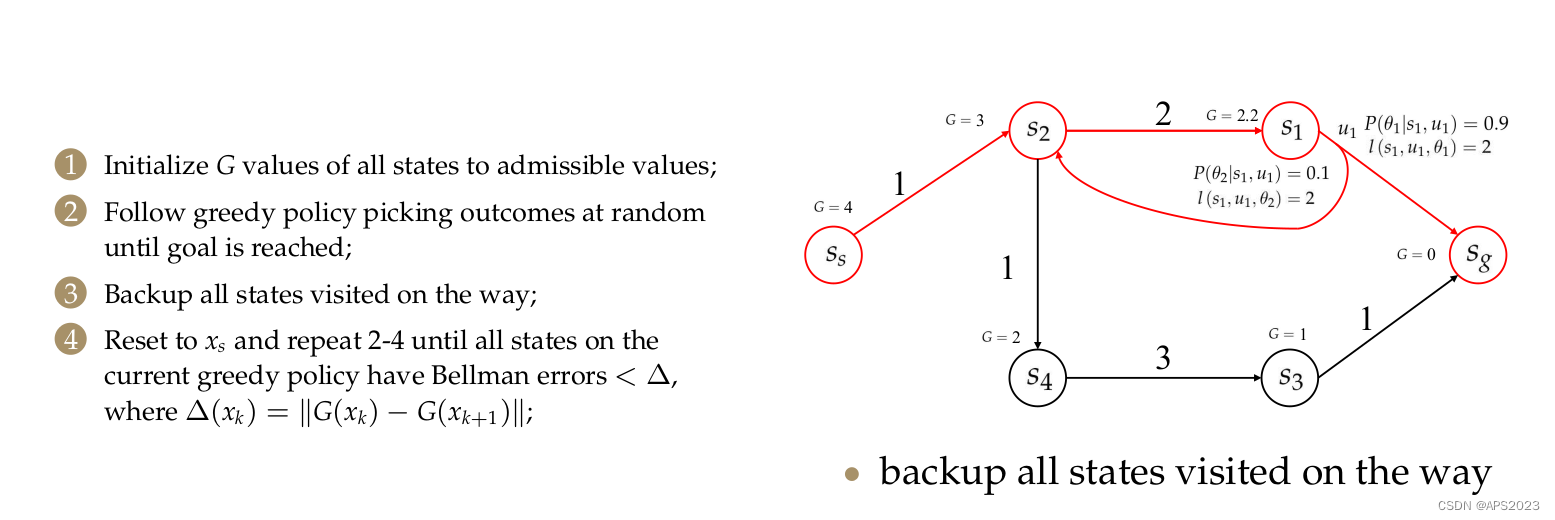
4 Real Time Dynamic Programming(RTDP)
看看实际例子吧:
根据每个节点到
的数量进行更新。