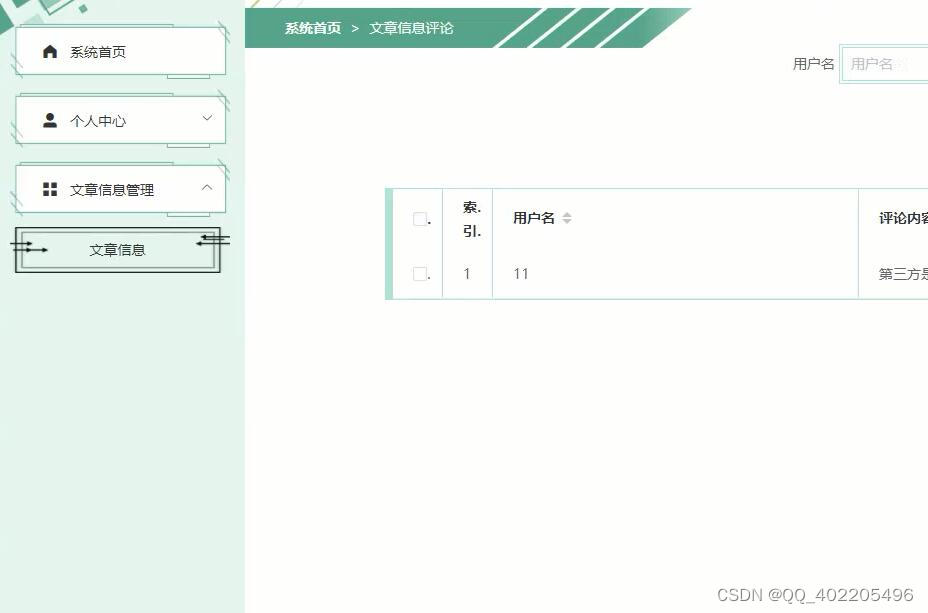
139.单词拆分
题目链接:
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
求解思路:
单词是物品,字符串s是背包,单词能否组成字符串s,就是问物品能不能把背包装满。
动规五部曲
- 确定dp数组及其下标含义:字符串长度为i,dp[i] 表示可以字符串可以拆分为一个或多个在字典中出现的单词
- 确定递推公式:如果确定dp[j] 是true,且[j, i]这个区间的子串出现在字典里,那么dp[i]一定是true。所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true
- dp数组的初始化:dp[0] = true,递推的根基;其他下表都初始化为false
- 确定遍历顺序:本题强调顺序,因此是排列问题,所以先遍历背包,再遍历物品;因为是完全背包,所以正序遍历
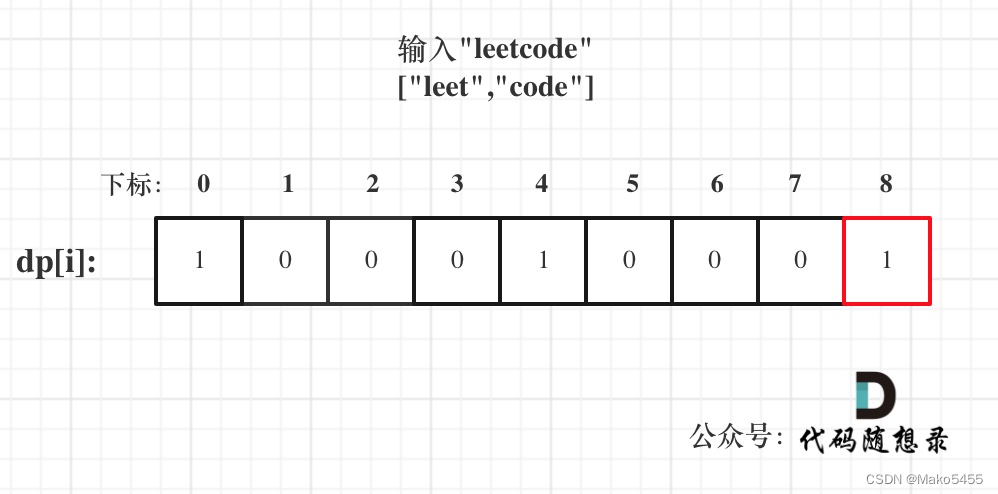
- 举例推导dp:以输入: s = "leetcode", wordDict = ["leet", "code"]为例,dp状态如图
代码:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordSet(wordDict.begin(), wordDict.end());vector<bool> dp(s.size()+1, false);dp[0] = true;for (int i = 1; i <= s.size(); i++){for (int j = 0; j < i; j++){string word = s.substr(j, i-j);if (wordSet.find(word) != wordSet.end() && dp[j]){dp[i] = true;}}}return dp[s.size()];}
};背包总结
背包递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数
遍历顺序
01背包
二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
完全背包
纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
求组合数
- 动态规划:518.零钱兑换II(opens new window)
求排列数
- 动态规划:377. 组合总和 Ⅳ (opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
求最小数
- 动态规划:322. 零钱兑换 (opens new window)
- 动态规划:279.完全平方数(opens new window)