目录
- 可解的条件 Solvability conditions on b
- 特解 A particular solution
- 通解 Complete solution
- 与零空间进行线性组合 Combined with nullspace
- 秩 Rank
可解的条件 Solvability conditions on b

矩阵 A 的第三行为第一行和第二行的加和,因此 Ax=b 中 b 的第 3 个分量也要等于其第 1 和第 2 个分量的和。若 b 不满足 b3=b1+b2则方程组无解。
检验 Ax=b 是否可解的方法是对增广矩阵进行行消元。如果矩阵 A 的行被完全消去的话,则对应的 b 的分量也要得 0。在本例中,矩阵 A 的第三行被消去:
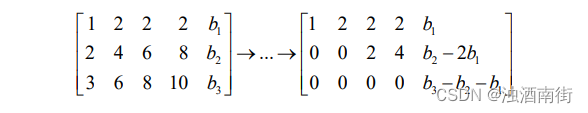
如果 Ax=b 有解,则 b3-b1-b2=0。在本例中我们令
A = [ 1 5 6 ] A=\begin{bmatrix} 1 \\ 5 \\ 6 \end{bmatrix} A= 156
可解的条件:只有当b处于矩阵的列空间C ( A )之中时,方程才有解。
等价的另一种描述方式为:矩阵A的行向量若经过线性组合为零向量时,则对应的b经同样的线性组合后也为0
特解 A particular solution
求 Ax=b 特解的方法是将自由变量均赋值为 0,求解其主变量。
本例中,令 x2=x4=0 得到方程组:
x 1 + 2 x 3 = 1 2 x 3 = 3 \begin{align*} &x1 + 2x3 =1 \\ &2x3 = 3 \end{align*} x1+2x3=12x3=3
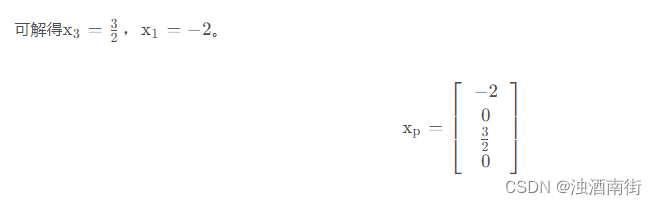
通解 Complete solution
为求得 Ax=b 的所有解,我们首先检验方程是否可解,然后找到一个特解。将特解和矩阵零空间的向量相加即为方程的通解。
与零空间进行线性组合 Combined with nullspace
A x p = b A x n = 0 A ( x p + x n ) = b \begin{align*} &Axp =b \\ &Axn = 0 \\ &A(xp+xn) = b \end{align*} Axp=bAxn=0A(xp+xn)=b
Ax=b 的通解为 xcomplete=xp+xn,其中 xn 为矩阵零空间中的一般向量。将Axp=b 和 Axn=0 相加可得 A(xp+xn)=b。
将A 转换成rref,则结果如下所示:

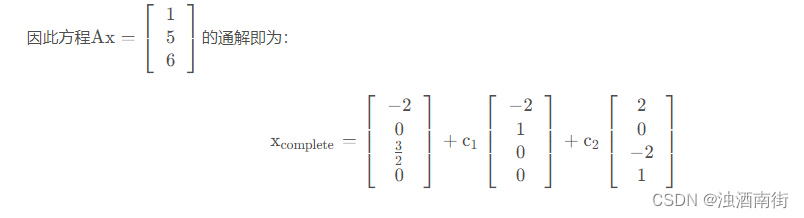
式中 c1和 c2为任意实数。 矩阵的零空间 N(A)是 R4空间中的二维子空间,方程的解 Ax=b 构成了穿过 xp点并和矩阵零空间平行的“平面“。但该”平面“并不是 R4空间的子空间。
秩 Rank
矩阵的秩等于矩阵的主元数。如果 mxn 矩阵的秩为 r,则必有 r<=m且r<=n。
讨论满秩(full rank)的情形:
• 列满秩:r=n。每列都有主元,x 的每一个分量都是主变量,没有自由变量。零空间 N(A)之内只有零向量。方程无解或者有唯一解 xp。
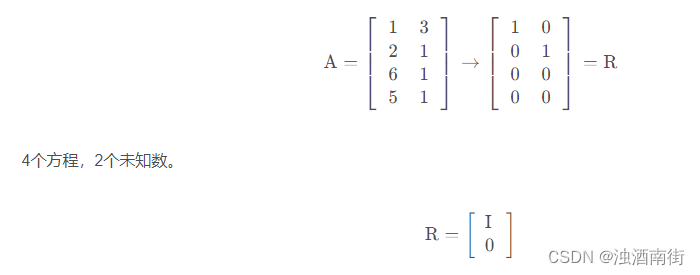
• 行满秩:r=m。每行都有主元,无论 b 取何值,方程 Ax=b 都有解。主变量 r 个,自由变量 n-r 个。
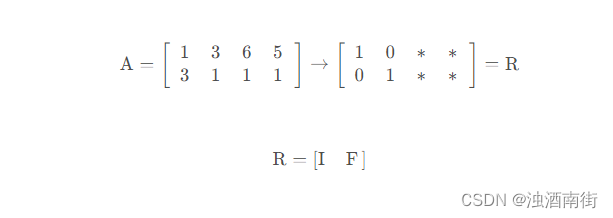
• 满秩 r=m=n,矩阵可逆。零空间只有零向量,无论 b 取何值,方程 Ax=b都有唯一解。
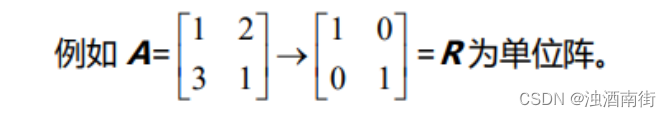
总结:

秩决定了方程组解的数量。