NOIP 冲刺之——数据结构-编程知识

NOIP 冲刺之——数据结构

news/2025/1/19 11:18:21/文章来源:https://www.cnblogs.com/Brilliant11001/p/18679419

$\texttt{0x00}$ 前言

本篇文章主要记录笔者 NOIP 冲刺阶段复习的各种数据结构题型及 tricks ans tips，同时也用于及时复习与巩固。

那么，开始吧。

$\texttt{0x01}$ 树状数组、线段树

知识点 $1$：二维偏序

众所周知，逆序对可以用归并排序离线求，但是要求在线呢？

这时候我们会想到树状数组。

P10235 [yLCPC2024] C. 舞萌基本练习

对答案二分一下，维护一个权值树状数组即可，需要注意的是每次询问完需要清空上一个区间的贡献。

树状数组求逆序对本质上是一种二维偏序，所以可以拓展到所有二维偏序的题型。

P10589 楼兰图腾

要求求出每个点左边有多少个大于、小于她的点，右边有多少个大于、小于她的点，正着反着各跑二维偏序一边相乘即可。

P1966 [NOIP2013 提高组] 火柴排队

一道有意思的题目。

首先需要一点前置的数学知识：排序不等式。

定理： 对于两个单调不降的有序数组 $\{a_1, a_2,\cdots,a_n\},\{b_1, b_2,\cdots,b_n\}$，那么有：

\[a_1b_1 + a_2b_2 + \cdots + a_nb_n\text{（有序和）} \]
\[\ge a_1b_{j_1} + a_2b_{j_2} + \cdots + a_nb_{j_n}\text{（乱序和）} \]
\[\ge a_1b_n + a_2b_{n - 1} + \cdots + a_nb_1\text{（反序和）} \]
证明：

观察式子 $a_1b_{j_1} + a_2b_{j_2} + \cdots + a_kb_{j_k} + \cdots + a_nb_{j_n}$.

考虑调整法，不妨设 $b_{j_k} = b_n$，现在将 $b_{j_k}$ 和 $b_{j_n}$ 交换位置，得到：

$a_1b_{j_1} + a_2b_{j_2} + \cdots + a_kb_{j_n} + \cdots + a_nb_{j_k}$.

上下两式做差得：

$a_k(b_{j_k} - b_{j_n}) - a_n(b_{j_k} - b_{j_n}) = (a_k - a_n)(b_{j_k} - b_{j_n})$.

$\because a_k \le a_n,b_{j_k} = b_n\ge b_{j_n}$.

$\therefore (a_k - a_n)(b_{j_k} - b_{j_n}) \le 0$，即：

\[a_1b_{j_1} + a_2b_{j_2} + \cdots + a_kb_{j_k} + \cdots + a_nb_{j_n} \le a_1b_{j_1} + a_2b_{j_2} + \cdots + a_kb_{j_n} + \cdots + a_nb_{j_k}$$.所以调整后和不减小，继续如上调整，至多调整 $n - 1$ 次就会得到同序和，证明完毕。 \]

回到原题，将式子转化为：$\sum\limits_{i = 1}^n(a_i^2 + b_i^2 + 2a_ib_i)$，而 $\sum (a_i^2 + b_i^2)$ 是个定值，所以只用考虑 $\sum(a_ib_i)$ 的值即可，发现她就是我们刚证明过的排序不等式！

通过这个定理我们就知道了要想得到最小的距离，就得让其最小，所以问题就变成了：让两盒火柴同序的最小操作次数。

看到是邻项交换，很容易想到逆序对，但是怎么转化呢？

仔细分析，发现根本不用管数值的绝对大小，只用考虑相对大小，所以可以考虑用离散化的思路。

发现问题的本质是：假设 $a$ 的第 $k$ 大数在位置 $i$，那么 $b$ 的第 $k$ 大数也要在位置 $i$。

那么先记录一下 $a,b$ 的每个位置上现在都是第几大的数，作为两个新的数组 $arank, brank$，然后让其中之一为标准，就变成逆序对问题了。

比如：$a = \{1, 3, 5, 2\}, b = \{1, 7, 2, 4\}$，那么 $arank = \{1, 3, 2, 4\}, brank = \{1, 4, 2, 3\}$，将 $arank$ 作为标准 $\{1, 2, 3, 4\}$，那么 $brank$ 变为：$\{1, 3, 2, 4\}$ 对其求逆序对即可。

P3431 [POI2005] AUT-The Bus

一眼动规，但是数据范围：$n,m\le 10^9$，直接去世了。
先离散化一下，但是直接 dp 还是 $O(k^2)$ 的，但是这是一看 dp 的状态还是 $O(k^2)$ 的，所以先考虑优化状态数。

将样例画出来看看：

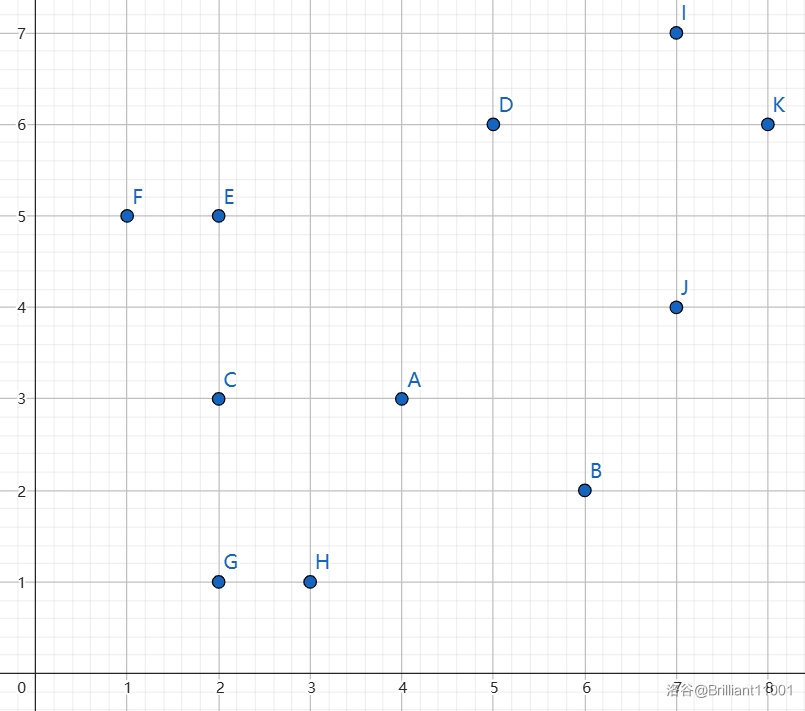
由于只能向上和向右走，所以一个点只能由她的左下角的点走来，很明显的二维偏序，这启示我们将点的坐标按 $x$ 为第一关键字升序排序，$y$ 为第二关键字升序排序，状态改为 $dp_i$ 表示考虑前 $1\sim i$ 个点，能接到的最大乘客数量。

那么树状数组优化一下转移就行了。

P2344 [USACO11FEB] Generic Cow Protests G

一道 dp 题，先推方程：$dp_i = \sum\limits_{j = 0}^{i - 1}dp_{j}[sum_i\ge sum_j]$。

直接转移显然是 $O(n^2)$ 的（但是这样也拿 90pts，数据太水了），观察到对 $dp_i$ 产生贡献的 $j$ 满足：$j < i,sum_j\le sum_i$，所以转换成二维偏序用树状数组优化转移就行了。

需要尤其注意！树状数组的下标不能为 $0$，否则会死循环，所以离散化的时候要把下标 $+1$。

[ABC327F] Apples

转化题意，发现需要维护一个矩形范围内的最大值，还是一样先用扫描线消掉一维，然后线段树维护另外一维即可。

P3605 [USACO17JAN] Promotion Counting P

给定一棵树，每个点都有一个权值，求出每个节点子树中权值比她大的点的数量。

本质上也是二维偏序，只是要倒过来计算。

直接维护一个树状数组，从根开始 dfs，保证了先遍历的点一定是后遍历的点的父亲，但这里不能直接计算了（因为贡献是在遍历当前点之后才可能产生），在遍历这个点之前查询一次，遍历完后再查询一次，两次做差就是这个点的答案。

知识点 $2$：用 dfn 序将树上问题转为序列问题

P3459 [POI2007] MEG-Megalopolis

给定一棵树，初始边权全为 $1$，现在需要维护之，支持两种操作：

操作一：修改某条边权为 $0$，保证每条边会被修改恰好一次；

操作二：查询某点到根节点的路径上的边权和。

操作简单，首先想到用 dfn 序将树上问题转换成区间问题，那么操作一就相当于区间修改，操作二就相当于查询前缀，用树状数组维护差分信息即可。

P3178 [HAOI2015] 树上操作

给定一棵树，根节点为 $1$，现在需要维护之，支持两三种操作：

操作一：将某个点权增加 $x$；

操作二：将某个子树的所有点权都增加 $x$；

操作三：询问某个节点 $x$ 到根的路径上的点权和。

操作一三都可以用 dfn 序差分直接做，但是操作二不太友好，推导一下。

当对节点 $x$ 进行子树加时，对于 $y\in \texttt{subtree(x)}$，$x\rightarrow y$ 这条路径会增加 $x\times (dep_y - dep_x + 1)$，这也是对 $y$ 节点的答案贡献，将原式分解成 $x\times dep_y - x\times (dep_x - 1)$，那么就可以开两个树状数组一个维护前者即 $dep_y$ 要乘以多少，一个维护后者即要减去多少就行了。

知识点 $3$：线段树维护"复杂"信息

P1471 方差

首先区间平均数容易维护，然后区间方差就推一推式子，得到：

\[s^2 = \frac{x_1^1 + x_2^2 +\cdots + x_n^2}{n} - \bar{x}^2 \]

然后再维护一个区间平方和就行了。

P4513 小白逛公园

单点修改 + 区间最大子段和。

因为父节点的和最大的子段可能会跨区间，所以不能直接维护最大子段和，这时候就需要分类讨论最大子段和的取值情况。

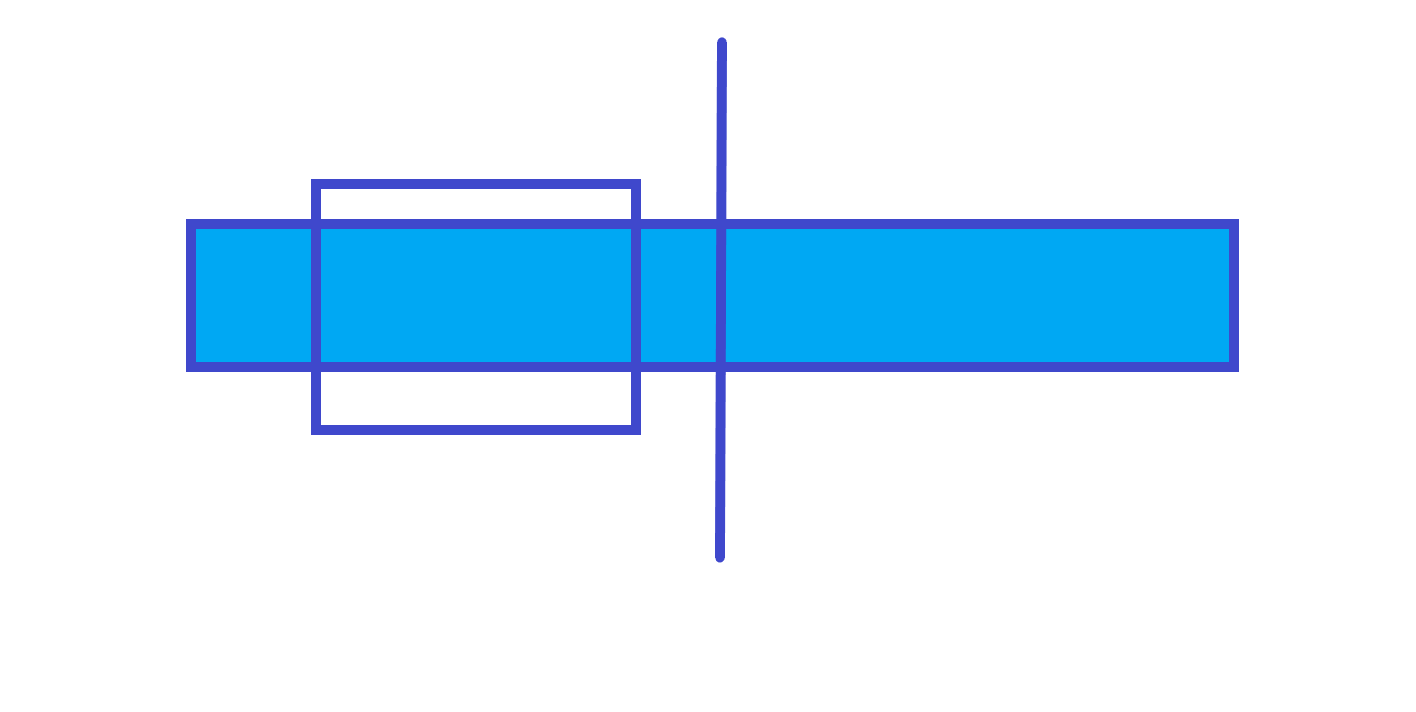
父节点的最大子段和在左儿子上。
父节点的最大子段和在右儿子上。
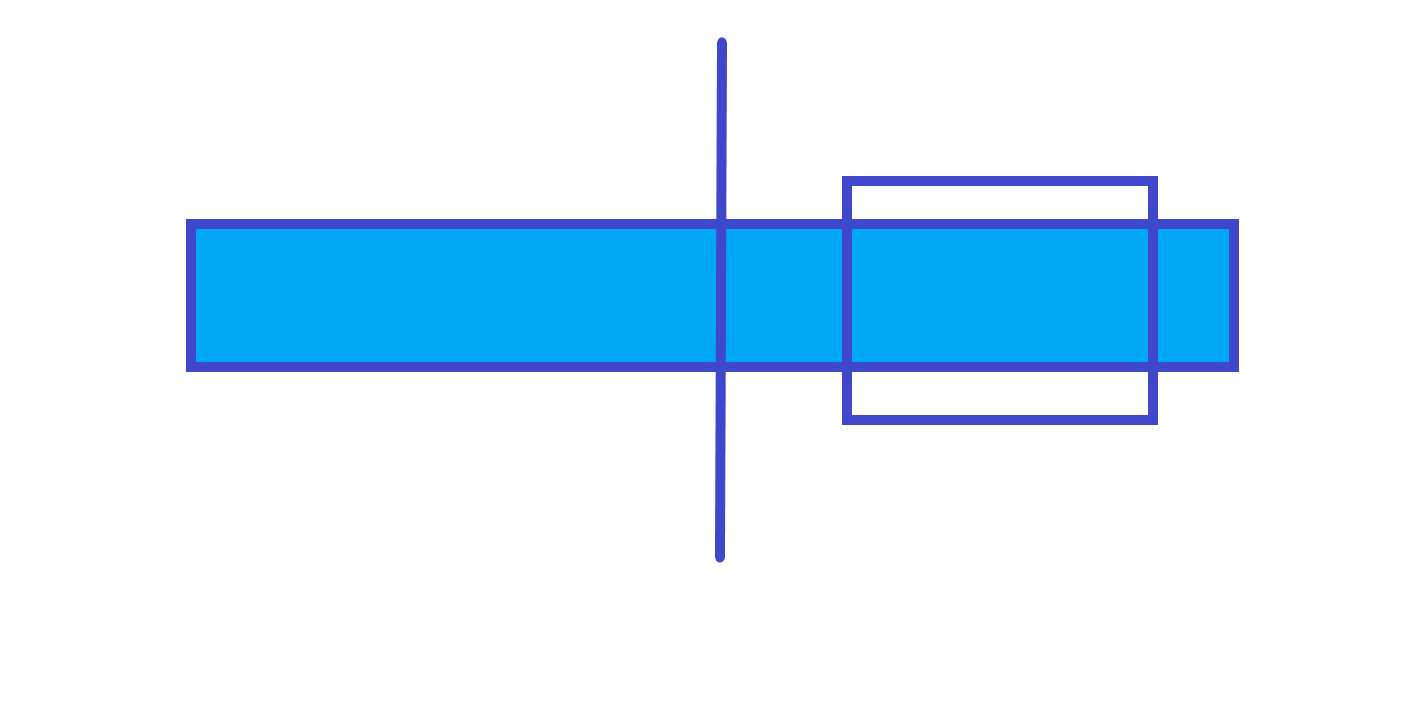
跨节点。

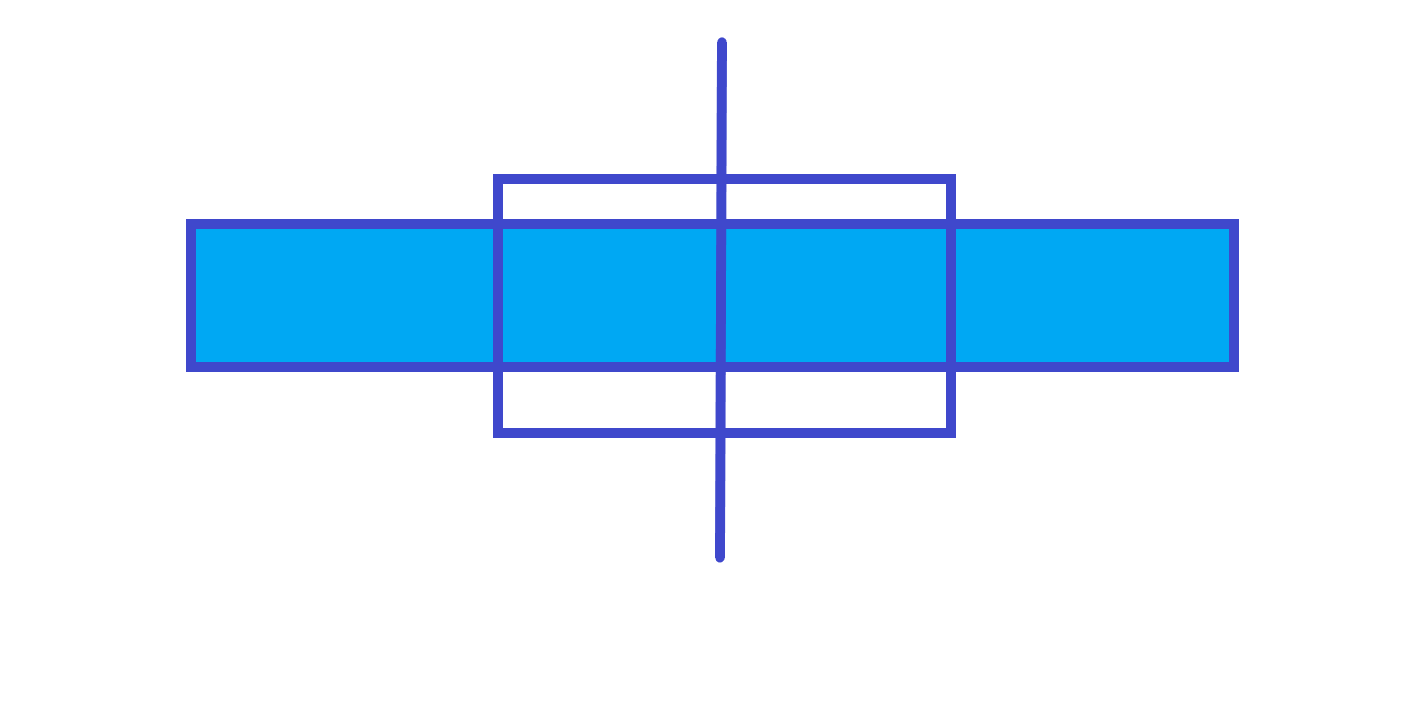
由以上三个图可知，父节点的最大子段和就是左儿子的最大子段和、右儿子的最大子段和和左儿子的最大后缀和 + 左儿子的最大前缀和三个中的最大值，所以我们可以再维护三个值：区间和，区间最大前缀和区间最大后缀。

首先区间和很好维护，那剩下两个怎么办呢？

还是分类讨论取值情况。（以最大前缀为例，最大后缀也是同理）

不跨区间
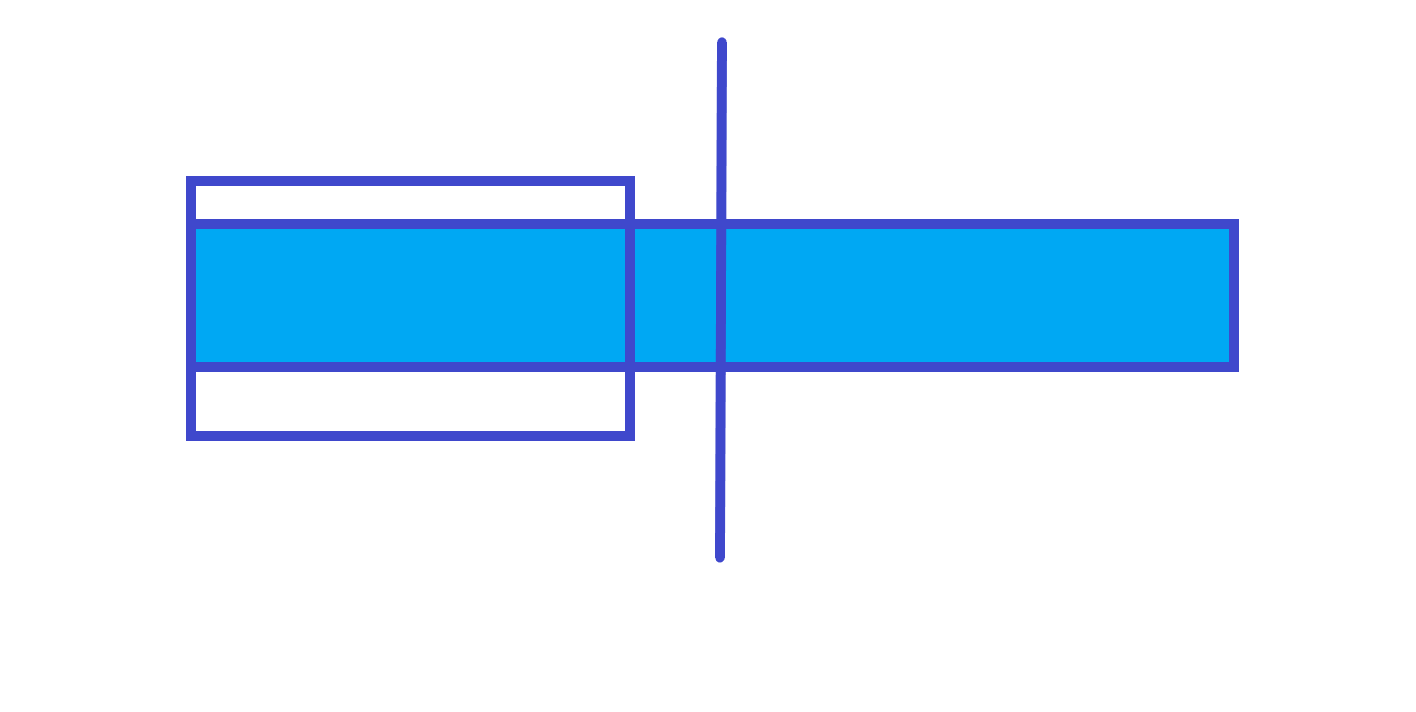
跨区间

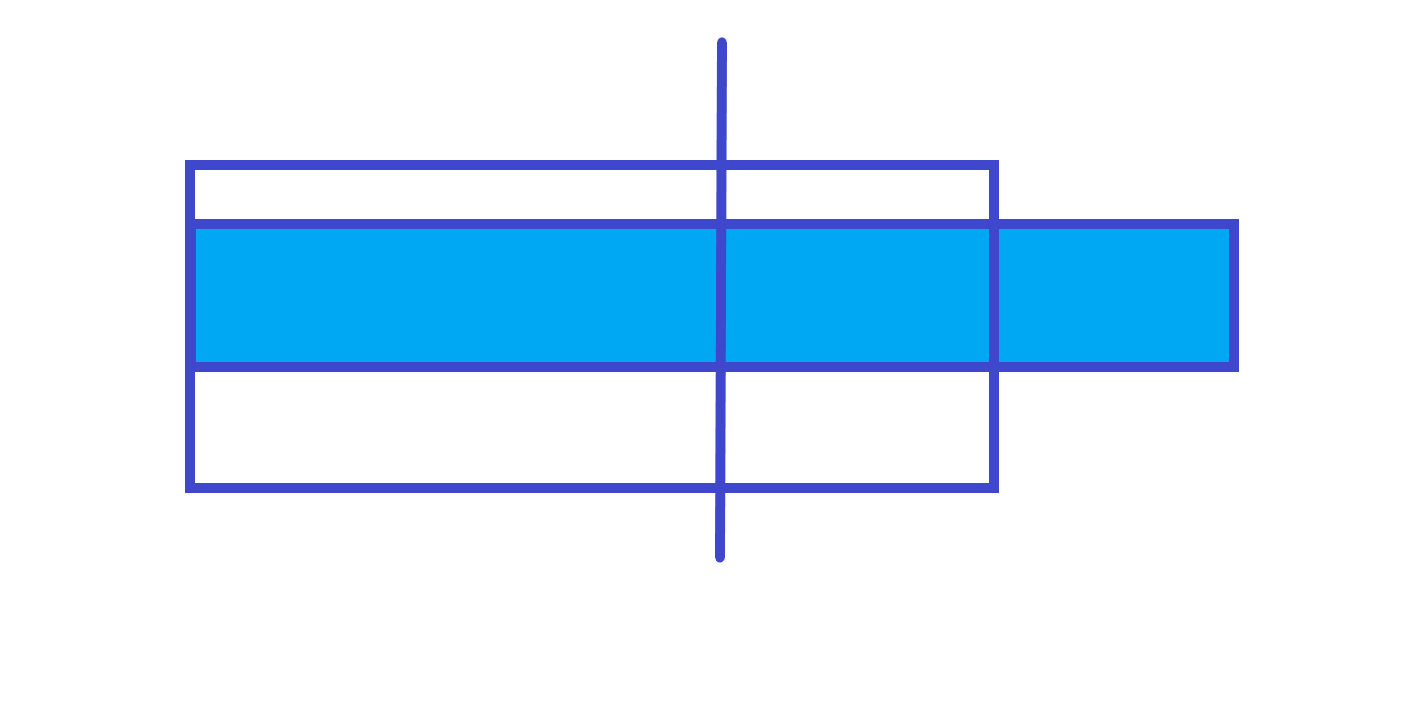
所以最大前缀和就是左儿子的最大前缀和和左儿子区间和 + 右儿子的最大前缀和的最大值。

上线段树模板维护即可。

P2572 [SCOI2010] 序列操作

需要四种操作：区间推平，区间取反，区间求和，区间求最大子段和。

维护一个推平的懒标记和取反的懒标记，注意顺序，在pushdown 时若是推平就把取反覆盖掉，若是取反就把推平反一下。

区间求和好办，区间连续 $1$ 的个数可以采用类似最大子段和的方式维护。

思路清晰也是可以一遍过的。

P6327 区间加区间 sin 和

合角公式：

\[\sin (\alpha + \theta) = \sin\alpha\cos\theta + \cos\alpha\sin\theta \]

\[\cos(\alpha + \theta) = \cos\alpha\cos\theta - \sin\alpha\sin\theta \]

推式子：

\[\begin{aligned} \sin (a_1 + d) + \cdots + \sin (a_n + d) &= \sin a_1\cos d + \cos a_1\sin d + \cdots + \sin a_n\cos d + \cos a_n\sin d\\ &= \cos d\cdot(\sin a_1 + \cdots + \sin a_n) + \sin d\cdot(\cos a_1 + \cdots + \cos a_n) \end{aligned}\]

那么可以维护在线段树中维护区间 $\sin$ 和和区间 $\cos$ 和，而且区间 $\sin$ 和我们已经知道如何维护。

区间 $\cos$ 和的维护也是同理，推一推式子就出来了。

P1382 楼房

线段树维护扫描线。

首先离散化，这里我选择是横着扫（早知道横着扫非常毒瘤我就竖着扫了）。

具体思路是将扫描所有竖着的线段，左侧为 $+1$，右侧为 $-1$，由于这道题要求输出轮廓上的转折点，所以线段树中维护目前覆盖到的最大高度。

这怎么保证这个最大高度一定是一个转折点呢？因为这道题维护的矩形都贴着 $x$ 轴，没有飘在天空中的房子（笑）。

~~奉承着维护扫描线从来不写 pushdown 的原则~~，我们维护一个 $cnt$，表示线段树上的这个节点被完全覆盖的次数。虽然有区间加，但是不可能为负，当 $cnt > 0$ 时，最大值就是右端点；否则就用左右儿子来更新最大值，若没有左右儿子呢？那就说明是叶子节点，未被覆盖，最大值为 $0$。

然后对于每一条线段，先查一下 $premx$，再执行对应的区间加，最后再查一下 $nowmx$，若 $premx \ne nowmx$ 再存答案。

怀着喜悦的心情写完，一遍过样例！交上去一看 WA 60pts，怎么回事？想了半天想不明白，去讨论区一看才发现有种特殊情况没考虑：假设有很多条线段重在一个位置，并且长短不一、有加有减怎么办？（这就是横着扫的下场）

这里给出数据：

没关系，单独讨论一下这种情况，发现这些线段可以一起考虑，先查一下 $premx$，然后把这个位置上所有的加减做完再看 $premx$ 和 $nowmx$ 就行了。

$\texttt{0x02}$ 并查集

并查集能在一张无向图中维护节点之间的连通性，这是它的基本用途之一。实际上，并查集擅长维护许多具有传递性的关系。

知识点 $1$：带权并查集

比如边带权的问题，就是多维护了每个点到她的目前的根节点即 $fa_x$ 的距离。

P1196 [NOI2002] 银河英雄传说

经典题目，维护到根的距离。

怎么维护？

首先是找祖先操作。

由于路径压缩，所以我们应该先更新当前点的祖先到新的根节点的距离，然后按当前点到根结点的距离就可以相加顺利得出。

int find(int x) {if(fa[x] == x) return x;int p = fa[x];find(p);d[x] += d[p];return fa[x] = fa[p];
}

接着是合并操作。

先找到要合并的这两个点 $x,y$ 的祖先，这时已经经过路径压缩，假设将 $x$ 放在 $y$ 的后面，那么 $d_y$ 不变，$d_x$ 变为 $siz_y$。

inline void merge(int x, int y) {d[x] = siz[y], siz[y] += siz[x], fa[x] = y;
}

查询操作直接模拟即可。

P5937[CEOI1999] Parity Game

将边权定义为：若 $d_x = 1$，则表示 $sum_x$ 与 $sum_{fa_x}$ 的奇偶性不同，否则表示相同。

然后就可以画图推理了。

P8779 [蓝桥杯 2022 省 A] 推导部分和

将边权定义为：若 $d_x = k$，则表示 $sum_x - sum_{fa_x} = k$。

知识点 $2$：种类并查集

也叫带拓展域的并查集。

P2024 [NOI2001] 食物链

用到了拆点的思想，将这 $n$ 只动物每个拆成 $3$ 个点，分别表示：同类，猎物，天敌，共 $3n$ 个点。

对于操作一，先检验 $x,y$ 是否互为猎物或天敌，若是则为假话，否则将两个动物的对应属性合并起来；

对于操作二，先检验 $x$ 是否被 $y$ 吃、$x$ 是否和 $y$ 是同一物种，若是则为假话，否则将 $x$ 的猎物和 $y$ 的同类合并，将 $y$ 的天敌和 $x$ 合并，还有最容易忽视的一点：由于$A,B,C$ 这三个物种是环状关系，所以 $y$ 的猎物是 $x$ 的天敌！，所以还应该将 $x$ 的天敌和 $y$ 的猎物合并。

知识点 $3$：启发式合并

虽然没有用到并查集，但是……不知道放哪了。

其实就是按 size 合并，每次把小的合并到大的里面，这样时间复杂度就是 $\log$ 的了。

为什么呢？因为每次合并后集合大小至少增加一倍。

P3201 [HNOI2009] 梦幻布丁

我们将每一种颜色看作一个集合，下标作为集合中的元素，那每次操作就是在合并两个集合。

询问的是颜色段数，这是可以 $O(n)\sim O(1)$ 的。

注意到一个很关键的性质：将所有颜色 $x$ 变为颜色 $y$ 和将所有颜色 $y$ 变为 $x$ 在只关心颜色段数时是等价的。

那么接下来就直接启发式合并就行了。

这里要注意一下，交换两个集合并不会改变其中下标在原数组中对应的颜色，所以在修改时需要先记录一下。

if(pos[x].size() > pos[y].size()) pos[x].swap(pos[y]); // 交换了下标但是 a 数组中的颜色还是没变
int col = a[pos[y][0]]; // 所以这里要先记一下
auto modify = [&](int p, int col) {ans -= (a[p] != a[p - 1]) + (a[p] != a[p + 1]);a[p] = col;ans += (a[p] != a[p - 1]) + (a[p] != a[p + 1]);
};
for(auto i : pos[x]) {modify(i, col);pos[y].push_back(i);
}

P4149 [IOI2011] Race

淀粉质经典题，但是不会淀粉质……

其实这道题有 dsu on tree 的做法。

dsu on tree 是维护子树信息的一种比较优秀的算法，核心思想是启发式合并。

这道题看似是路径问题，但是可以转化成子树信息的维护。

我们不妨这样想，在一个以 $root$ 为根的子树中是否存在经过点 $u$，长度为 $k$ 的路径，若这条路径 $u\rightarrow v$ 存在，则可以用 lca 转化 $dep_u + dep_v - 2\times dep_{root = lca(u, v)} = k$，那么可以考虑在 $root$ 的一个儿子中枚举点 $u$，然后查询有没有其他儿子中的一个点 $v$，满足上式，即查询有没有点 $v$ 使得 $dep_v = k + 2\times dep_{root} - dep_u$，这个用 hash table 可以办到。

理一下思路，dfs 整棵树，预处理出每个点到根节点的边权和 $dep1$、边数 $dep2$ 和重儿子 $hs$。

然后再 dfs 一遍，先进入 $u$ 的一棵子树进行枚举，查询同时更新最小的边数，然后将这一棵子树中的点加入 hash table，然后看下一棵子树……以此类推直到遍历完所有子树，最后再查询根节点 $u$ 出发是否有满足的路径，并加入。

这种做法显然是 $O(n^2)$ 的，考虑用 dsu on tree 优化。

根据启发式合并的思想，我们每次处理一个子树时，可以把轻儿子一个一个暴力地合并到重儿子上，最后再让根节点继承重儿子的信息。由于轻儿子的信息已经暴力加到重儿子中了，所以我们只保留重儿子的信息，轻儿子的就可以删掉了。

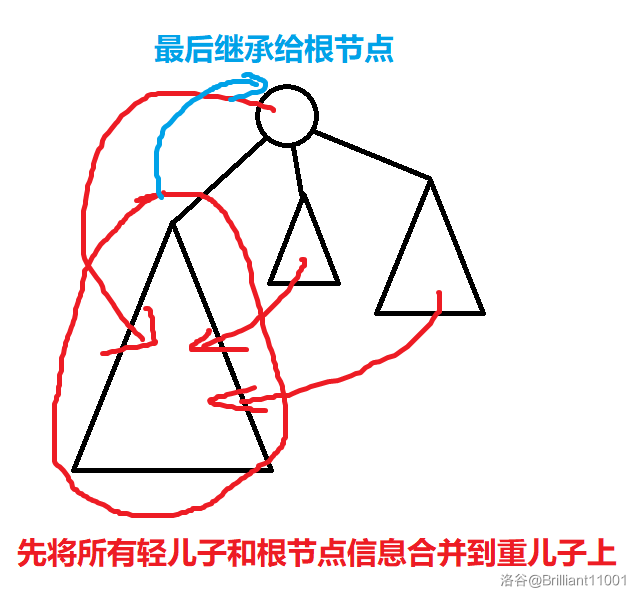
这样时间复杂度就变成了 $O(n\log n)$。

顺便贴一下 dsu on tree 的标准模板：

// 这里还求了 dfs 序，主要是为了减小后续遍历儿子的常数
void dfs(int u, int fa) {l[u] = ++tim, id[tim] = u;siz[u] = 1, hs[u] = -1;for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa) continue;dep1[j] = dep1[u] + 1;dep2[j] = dep2[u] + w[i];dfs(j, u);if(hs[u] == -1 || siz[j] > siz[hs[u]])hs[u] = j;}r[u] = tim;
}// keep 表示当前的信息是否保留
void dfs2(int u, int fa, bool keep) {//从下往上算for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa || j == hs[u]) continue;dfs2(j, u, false);}// 若有重儿子，则先收集她的信息if(~hs[u]) dfs2(hs[u], u, true);auto query = [&](int x) {...};auto modify = [&](int x) {...};auto del = [&](int x) {...};// 遍历轻儿子for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa || j == hs[u]) continue;for(int x = l[j]; x <= r[j]; x++) query(id[x]);for(int x = l[j]; x <= r[j]; x++) modify(id[x]);// 一定是先遍历完整棵子树再修改，否则可能找到此棵子树里的值}// 最后添加根节点query(u), modify(u);// 若不保留信息就删掉if(!keep)for(int x = l[j]; x <= r[j]; x++) del(id[x]);
}// 主函数调用
dfs(1, -1);
dfs2(1, -1, false);

她还是挺套路的，就和莫队一样，转化完之后就可以直接无脑打，而且她们都只能离线下来做。

dsu on tree 和莫队同属于优雅的暴力算法！

其他：

咕咕咕……

$\texttt{0x03}$ 单调队列、单调栈、RMQ

单调队列主要提前排除无用决策，主要用来优化 dp。

P2569 [SCOI2010] 股票交易

先想暴力，设 $dp_{i, j}$ 表示到第 $i$ 天，现在手上还有 $j$ 股，能获得的最大利润，设交易冷却期为 $W$。

将当前的操作分为四种：

空仓买入；
持股不操作；
持股买入；
卖出。

第一种操作就是赋初始值：$dp_{i, j} = -ap_i\times j$；

第二种操作就是继承上一个状态：$dp_{i, j} = dp_{i - 1, j}$，这个更新至关重要的一点是她为后来的操作提供了方便；

第三种操作从背包的角度考虑，设买入了 $k$ 股，那么转移方程为：$dp_{i, j} = dp_{i - W - 1, j - k} - k\times ap_i$。注意！这里之所以没用 $1\sim i - W - 1$ 转移是因为我们在第二种操作时就已经包含了前面几天的所有决策，所以直接用 $i - W - 1$ 转移就行了。

第四种操作类似，设卖出了 $k$ 股，那么转移方程为：$dp_{i, j} = dp_{i - W - 1, j + k} + k\times bp_i$。

这样是 $O(n^3)$ 的，考虑优化。

发现当 $j$ 增加 $1$ 时只增加了一个决策 $dp_{i - W - 1, j}$ 同时可能减少若干决策，所以可以往单调队列优化的方向思考。

将操作 $3,4$ 的式子转化一下，得：

操作 $3$：$dp_{i, j} + j\times ap_i = dp_{i - W - 1, k} + (j - k)\times ap_i$

操作 $4$：$dp_{i, j} + j\times ap_i = dp_{i - W - 1, j + k} + (j + k)\times bp_i$

对于操作 $3$，将 $dp_{i, j} + j\times ap_i$ 看作一个整体，相当于求滑动窗口区间最大值，就可以用单调队列维护了，操作 $4$ 也是同理。

单调栈见得少，感觉主要在求左右最近的大于/小于它的数/位置。

咕咕咕……

RMQ 问题就比较广泛了，最常见的静态写法就是 st 表，动态的话就上线段树。

稍微拓展一下，st 表其实可以维护带有结合律和交换律的信息，比如区间 $\wedge,\vee,\gcd$ 等。

P2471 [SCOI2007] 降雨量

一道分类讨论的好题。

首先把年份和降雨量存下来离散化，对于每组询问：

若年份 $x,y$ 未收录，那么一定是 maybe。
若年份 $y$ 未收录，但年份 $x$ 被收录，那么只能是 false 或 maybe。找到 $y$ 的后面第一个被收录的年份 $y'$，若 $y'$ 到 $x$ 的降雨量最小值严格小于 $x$ 年的降雨量就是 maybe，否则就是 false。
若年份 $x$ 未收录，但年份 $y$ 被收录，这里有一个极其容易被忽略的一点（可能就我忽略了），找到 $x$ 年前第一个被收录的年份 $x'$，若 $y$ 到 $x'$ 之间的最大降雨量已经大于等于 $y$，那么不管 $x$ 降雨量为何值都不可能了，这时候 false，否则 maybe。
若年份 $x,y$ 都被收录到了，那么就判一下中间的已收录年份是否连续，若连续且上述条件都满足就是 true，否则若不连续但条件都是满足的就是 maybe，否则就是 false。

对于不带修的 RMQ 用 st 表真是再好不过了！

$\texttt{0x04}$ $\texttt{Trie}$

知识点 $1$：字典树

太简单就不贴题了，咕咕咕……

知识点 $2$：$\texttt{01 Trie}$

2.1 序列异或最大值

P10471 最大异或对

暴力做法显然是 $O(n^2)$ 的，考虑优化。

我们不妨从异或的定义（或者说本质）来思考。异或运算实际上是将要运算的两个数分别写成二进制形式，然后逐位计算。

这启示我们可以将所有数转化成二进制形式来思考，什么时候异或得到的值最大呢？当然是同一二进制位上不相同的时候！

举个例子，一个数的第 $k$ 个二进制位上是 $1$，那么我们应该尽量挑选第 $k$ 个二进制位上是 $0$ 的数和它运算。对于这个数的所有位我们都这样贪心地考虑，就能找到异或的最大值了。

然后你就会发现这个过程和 $\texttt{trie}$ 的查找方式极其相似！

将每个 $a_i$ 插入，然后对于每个 $a_i$ 遍历，根据刚刚所说的尽量走相反的节点即可。

2.2 序列异或第 $k$ 小

题目描述：

给定序列 $\{a_n\}$，$m$ 次询问，每次给出 $x,k$ 需要回答 $a_1\oplus x,a_2\oplus x,\cdots,a_n\oplus x$ 的第 $k$ 小。

在 $\texttt{01 Trie}$ 上二分。先将序列 $a$ 中的所有数插入，在询问时先考虑能否使答案的这一位为 $0$，即看一下这个子树的大小够不够 $k$，若可以则走过去，否则走另一边，并且将 $k$ 减掉子树大小。（这个思路和线段树上二分是一样的）

$\texttt{Code}$

$\texttt{0x05}$ 平衡树

来不及复习啦/qaq。（我就猜不会考）

$\texttt{0x06}$ 可持久化数据结构

来不及复习啦/qaq。（反正听说不考）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/871646.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

windows 将docker desktop上镜像打包并通过资源管理器找到使用