LFM信号分析-编程知识

LFM信号

在时域中，理想线性调频信号持续时间为 $T$ 秒，振幅为一常量，中心频率为 $f_{center}$ ，相位 $\theta(t)$ 随时间按一定规律变化。当 $f_{center}$ 为0时，信号的复数形式为

$\left( \frac{t}{T} \right) e^{ j \pi K t^2 }$

其中， $t$ 是时间变量， $K$ 是线性调频率，单位为 $Hz / s$ 。

瞬时频率：

$f = K t$

由于频率的线性调制，相位是时间的二次函数：

$\phi(t) = \pi K t^2$

信号带宽是斜率及其持续时间的乘积：

$\left| K \right| T$

时间带宽积(TBP)是带宽和持续时间的乘积，该参数是无量纲的：

$\left|K\right| T^2$

线性调频信号的频谱，难以直接推导，可利用驻定相位原理得到简单的近似表达式。

驻定相位原理(POSP)：

信号相位包含二次及更高次，在相位驻留点附近是缓变的，而在其他时间点上是捷变的，相位捷变处由于相位周期的正负部分相互抵消，故其对积分的贡献几乎为零，对积分起主要作用的部分集中在相位驻留点附近。

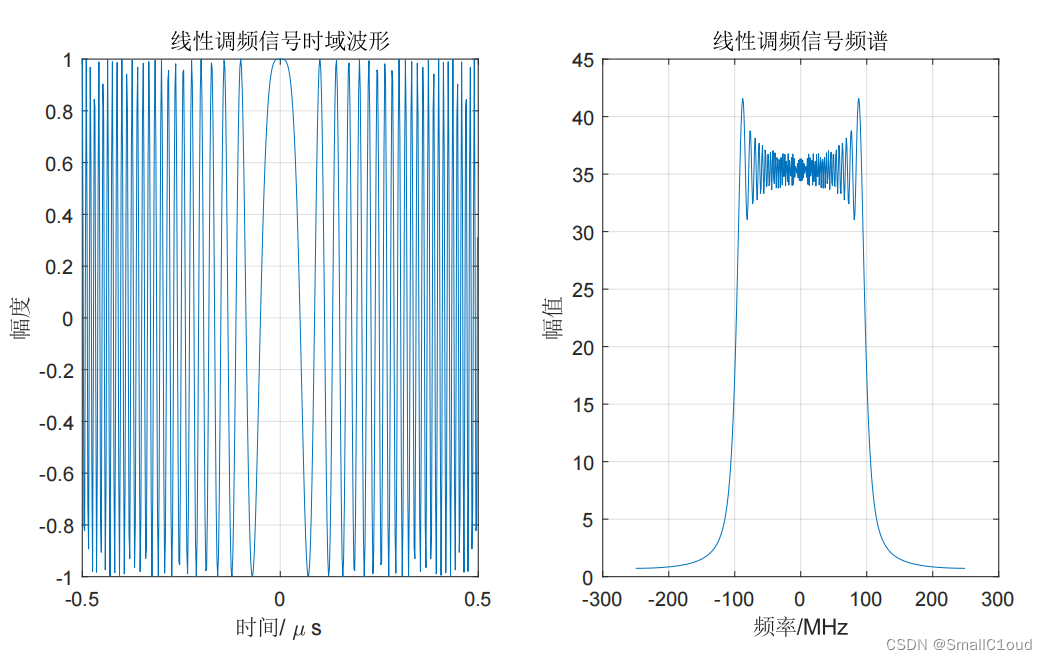
信号带宽为200MHz，脉冲持续时间为 $\mu s$ ，过采样率取 $\alpha_{os}=1.25$ 时的基带LFM信号的时域波形和频谱图如下图所示。

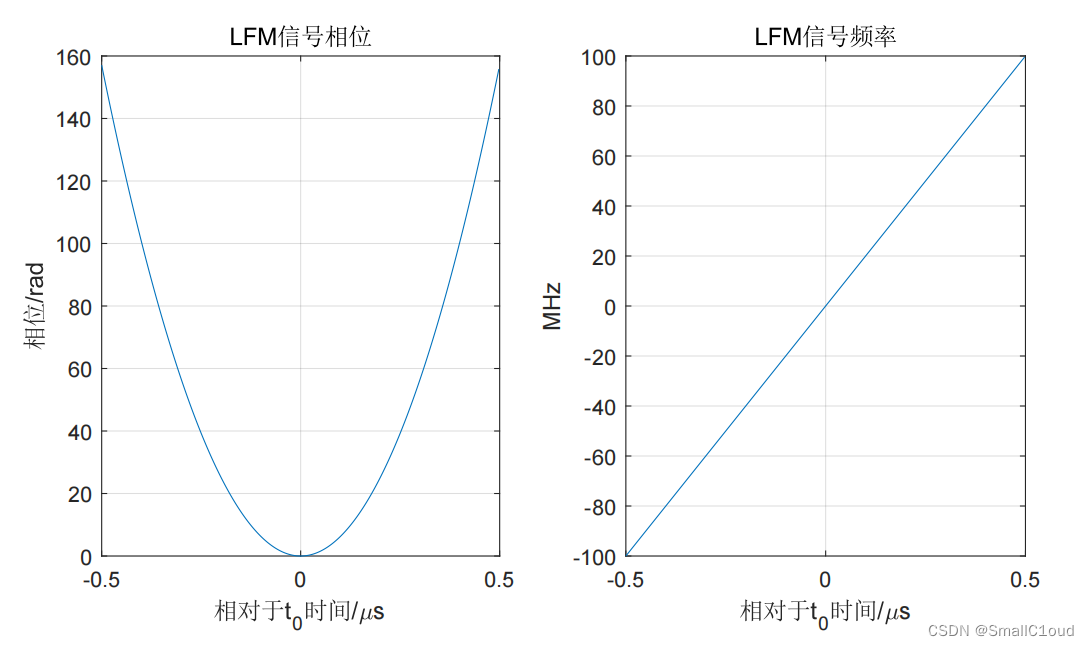
在这里插入图片描述

下图给出了基带LFM信号的瞬时相位和瞬时频率，其相位是二次的，其频率是时间的线性函数，频率斜率是线性调频率，由于和鸟鸣很相似，故线性调频信号常被称为Chirp信号。

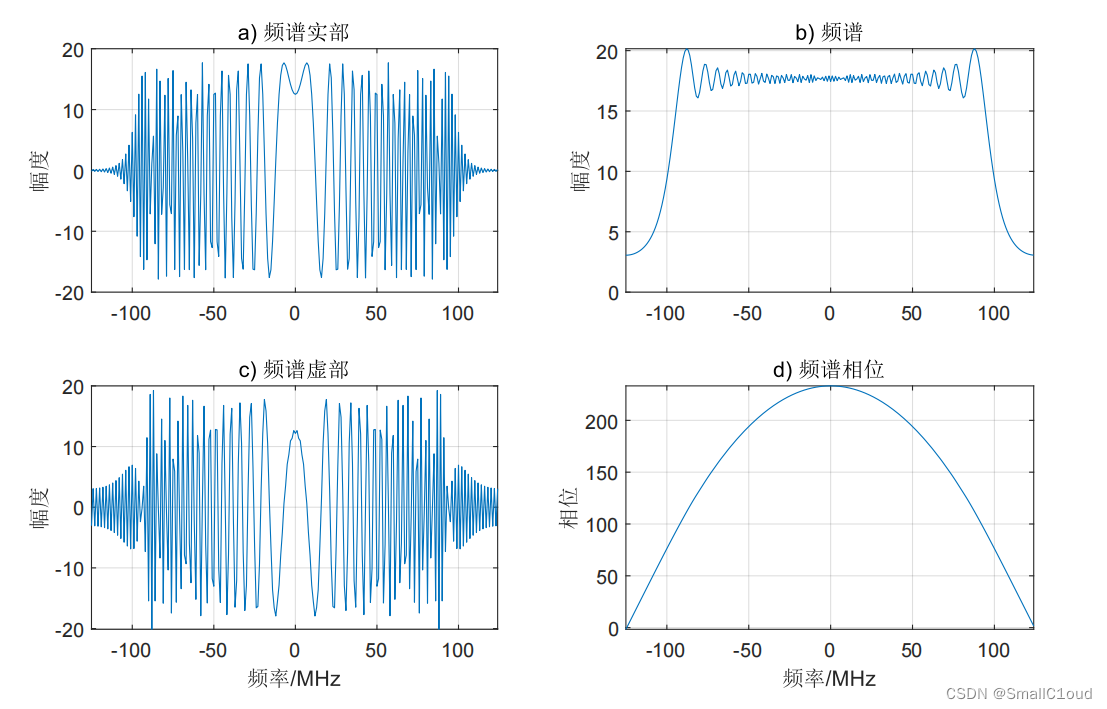
在这里插入图片描述

下图给出了TBP=200时，过采样率 $\alpha_{os}=1.25$ 时通过DFT而不是POSP得到的线性调频脉冲频谱，由于在DFT后进行了 $ff t s hi f t$ (左/右半边互换)操作，故零频位于序列中心。可以看出，频谱的实部和虚部具有和LFM相似的线性调频结构，与LFM信号不同的是频谱存在 $\pi / 4$ 的相位差，且调频率发生了变化；频谱的幅度可以近似为矩形窗函数；频谱的相位与LFM信号的相位基本一致，可近似为一个关于频率的二次函数。

在这里插入图片描述

探究不同过采样率下的DFT结果

基带复线性调频信号的最高频率为带宽的一半，所以最低复采样率 $f_s$ 必须大于带宽。检验采样率充分性的另一种方法就是寻找采样信号频谱中的间隙，如果间隙不存在，则采样率过小；如果间隙高于采样率的20%，采样率就大于最优效率值。

为了衡量能量间隙的相对大小，定义过采样因子为 $\alpha_{os} = \frac{f_s}{\left|K\right| T }$

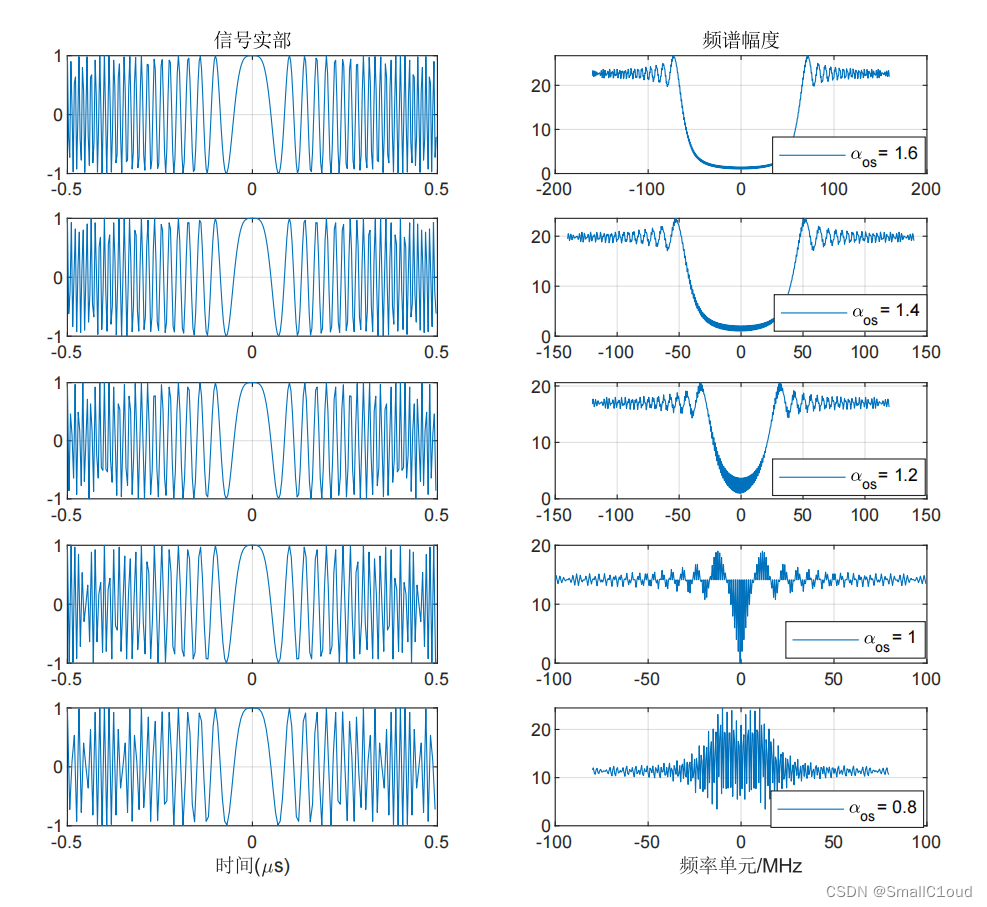
图 \ref{不同过采样率下的信号实部和频谱幅度-在频谱中引起的能量间隙} 给出了不同过采样率下LFM信号补零后的能量间隙。可以看出：随着过采样率以0.2的间隔逐步降低，能量间隙也相应减少，间隙也可以看成是未被利用的频谱空间。 $\alpha_{os}=1.2$ 时，频谱中存在一个很小但很清晰的间隙，说明此时这一过采样值较好地兼顾了效率和精度； $\alpha_{os}=1$ 时，间隙消失，虽然严格来说此时不会出现混叠，但由于存在标称带宽范围外的频率泄露，仍会发生少量混叠；当 $\alpha_{os}=0.8$ 时，存在严重的混叠，较低和较高部分的频谱交织在一起，无法区分。因此为了保留连续信号的信息， $\alpha_{os}$ 必须大于1，通常取在 1.1 ~1.4之间。

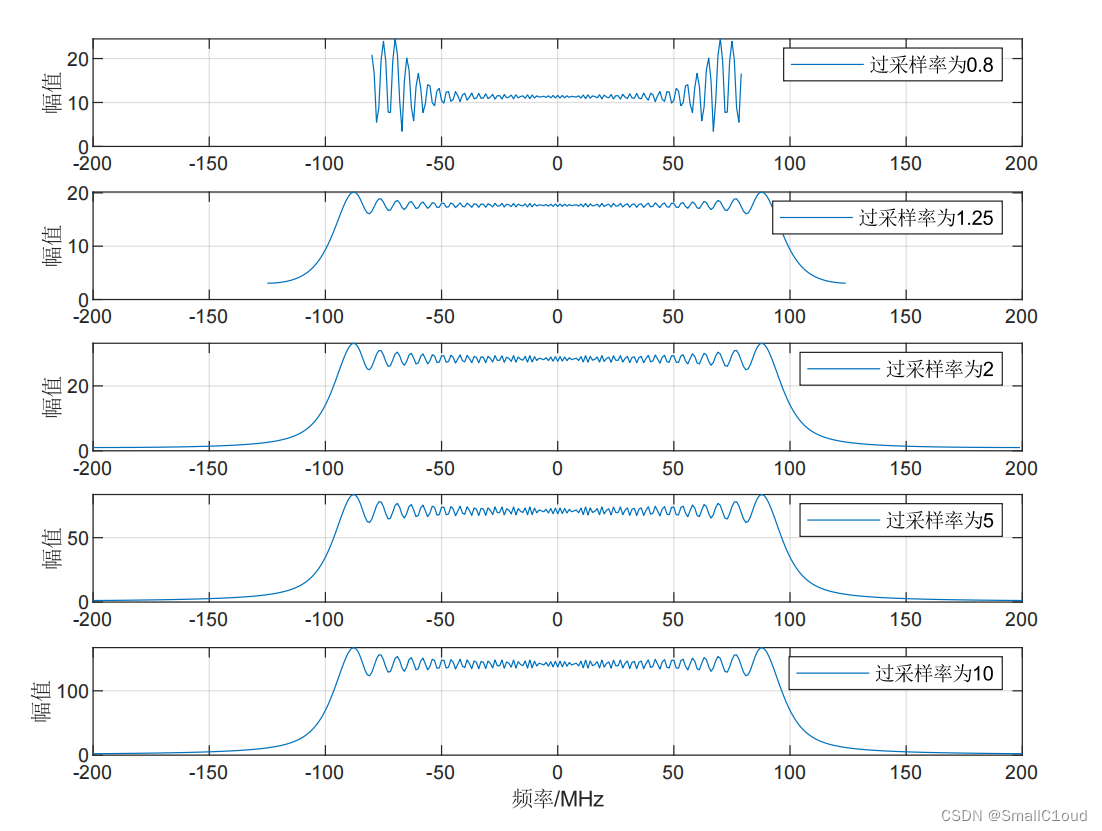
在这里插入图片描述
下图给出了不同过采样率下的信号频谱，当 $\alpha_{os}=0.8$ 时，采样率不足以恢复出原信号，其对应的频谱缺失了一部分；当 $\alpha_{os}>1$ 时，能较好地恢复原信号，频谱近似于矩形窗。实际中，为了有效利用数据点数，同时保证能正确恢复信号，通常取 $\alpha_{os} \approx 1.2$ 。

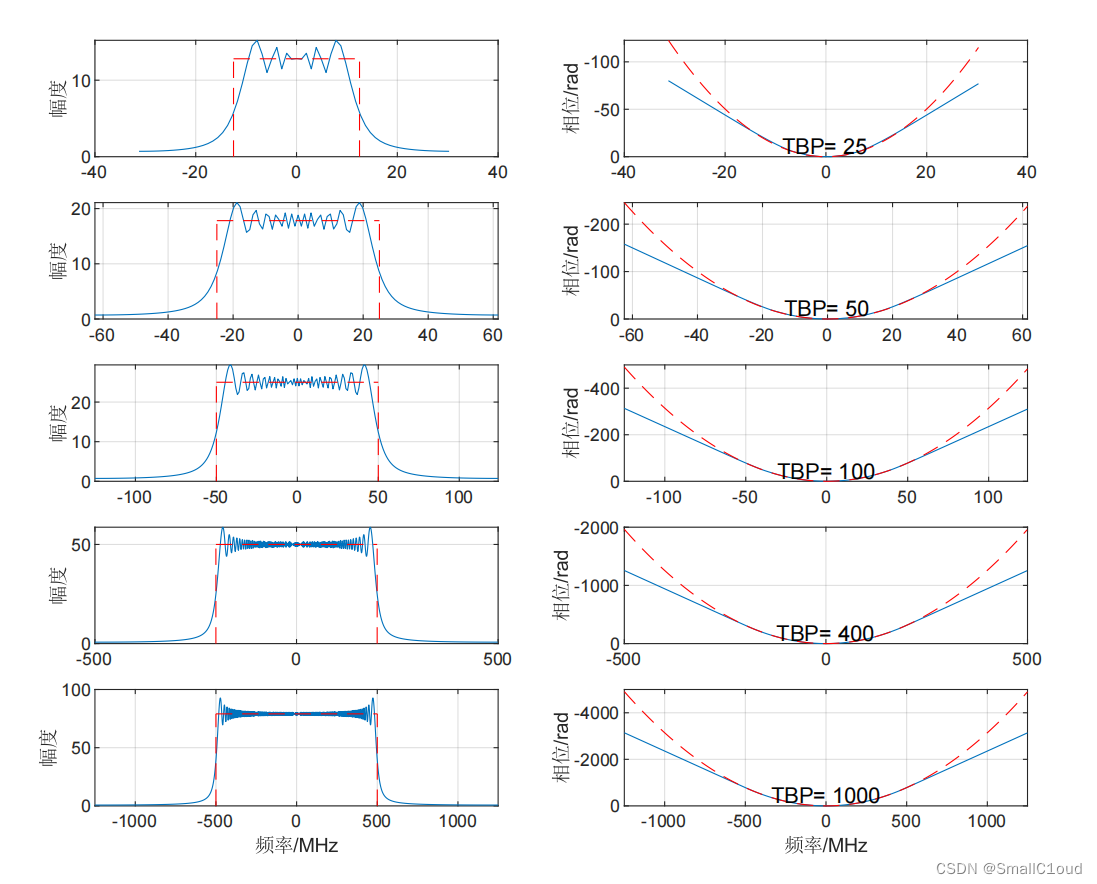
在这里插入图片描述

下图给出了不同TBP时的LFM信号频谱图，由左边一列可以看出，随着TBP的增大，信号频谱幅度越接近矩形窗，当TBP<100时，近似效果较差；TBP>100时，近似效果较好，且随着TBP的增大，频域上的吉布斯效应不会消失。在SAR信号处理中，通常取较大的TBP。

在这里插入图片描述

统计指标

IRW冲激响应宽度，指冲激响应的3dB宽度，其数值等于脉冲分辨率，时间量纲下的3dB分辨率可以表示为
$\rho = \frac{0.886}{| K | T} \approx \frac{1}{| K | T}$

PSLR最大旁瓣与主瓣峰值的高度比，称为峰值旁瓣比。
$PSLR=10log_{10} \left( \frac{P_{sidelobe}}{P_{mainlobe}} \right)$

ISLR积分旁瓣比，旁瓣能量与主瓣能量的比值(计算中主峰和旁瓣以靠近峰值的两个零点为分界线)
$ISLR=10log_{10} \left( \frac{P_{total}-P_{main}}{P_{main}} \right)$

基带LFM信号脉冲压缩的实现

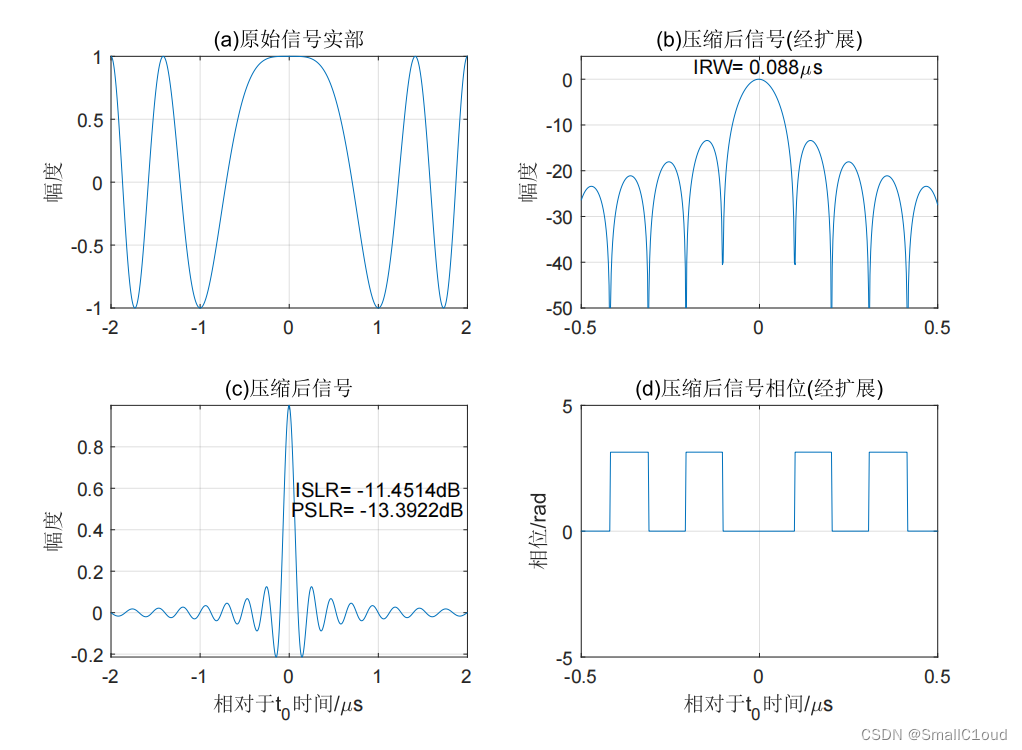
下图给出了基带LFM信号的脉冲压缩示意，信号长 $10\mu s$ ，TBP为100。图\ref{基带LFM信号的脉冲压缩abcd}(a)给出了原始信号实部；由图(b)可以看出，压缩脉冲3dB宽约为 $\mu s$ ，压缩比和TBP近似相等，约为100；图中©给出了经脉冲压缩后的峰值旁瓣比(PSLR)约为-13dB，积分旁瓣比(ISLR)约为-11.5dB；由于不含噪声，故主瓣及偶数旁瓣中的相位为零。

在这里插入图片描述

探究频域加窗的影响

由于线性调频信号存在一一对应的时频关系，所以可以在时域加窗，还可以在时域设计无窗匹配滤波器，直至在频域处理数据时再加窗。

频谱为矩形窗时，对应的时域脉冲的峰值旁瓣比(PSLR)为-13.2 $d B$ ，一般认为这一PSLR过高，因为在图像中会淹没附近的弱目标。实际SAR处理中，通常要求PSLR在-20 $d B$ 以下，ISLR在-17 $d B$ 以下，降低PSLR的一种方法是在频域引入平滑窗，以减少主瓣到旁瓣的能量泄露，从而避免弱目标主瓣被临近强目标的旁瓣淹没。

典型窗包括Taylor窗、Chebyshev窗、Hanning窗、Hamming窗和Kaiser窗。本节主要仿真分析了Hanning窗、Hamming窗和Kaiser窗对脉冲压缩的影响。

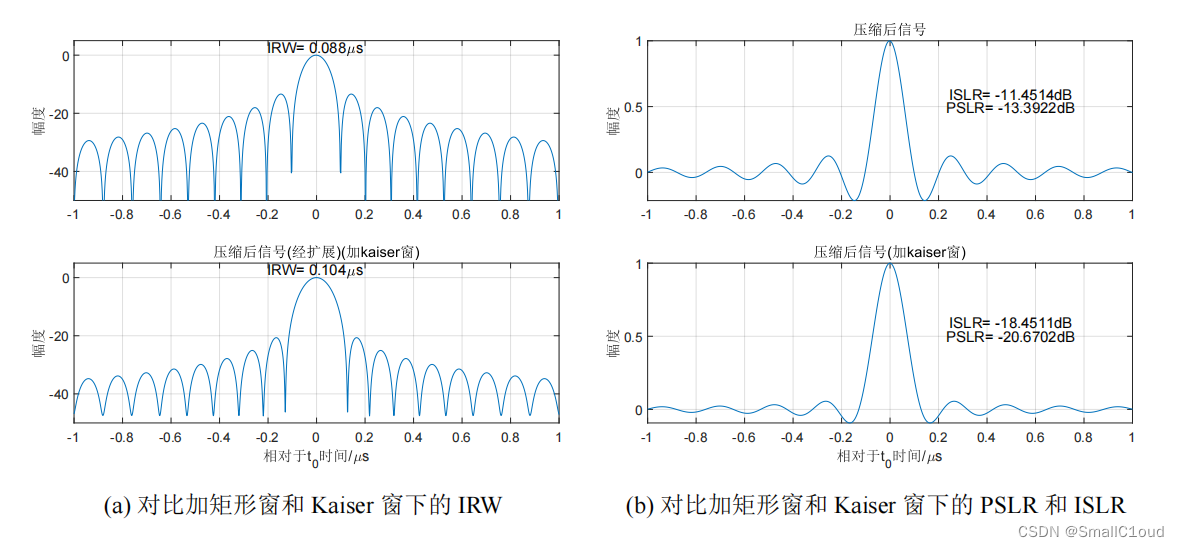
Kaiser窗是一种似长球波函数，其能在一定的ISLR下，近乎最优地使脉冲压缩的主瓣能量达到最大；Kaiser有一个可调节参数 $\beta$ ,可以在不同应用中兼顾分辨率和旁瓣。下图给出了在 $\beta = 2.5$ 时加矩形窗(Kaiser窗的 $\beta = 0$ 时即为矩形窗)和Kaiser窗的对比，与矩形窗相比，Kaiser窗将PSLR降低至-20.67dB(近似为幅度的1/10)，ISLR降低至-18.45dB，但分辨率扩展了1.18倍，由于窗的展宽效应可以抵消式\ref{脉冲分辨率}中的0.886，故其可忽略不计。.

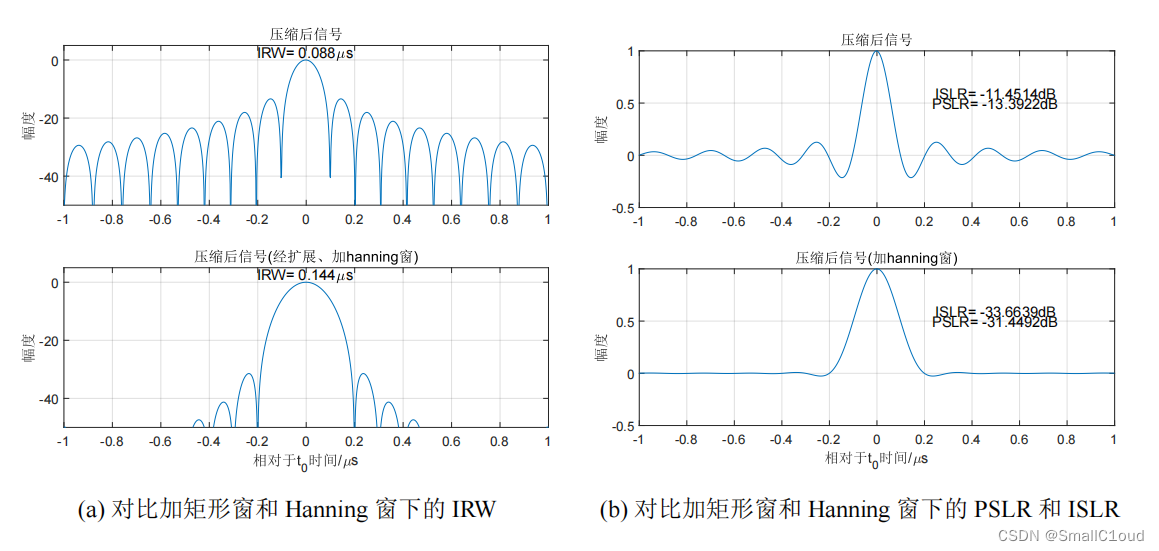
在这里插入图片描述
下图给出了矩形窗和加Hanning窗的脉冲压缩结果，与矩形窗相比，Hanning窗将PSLR降低至-31.45dB，有效地抑制了副瓣的幅度，有利于提高信号的动态范围；ISLR降低至-33.66dB，使得能量集中在主瓣当中；分辨率扩展了1.64倍，一定程度上降低了分辨能力。总的来说，使用Hanning窗进行频域加窗处理可以改善脉冲压缩的副瓣抑制效果，但会导致脉冲宽度的增加(即分辨率降低)。

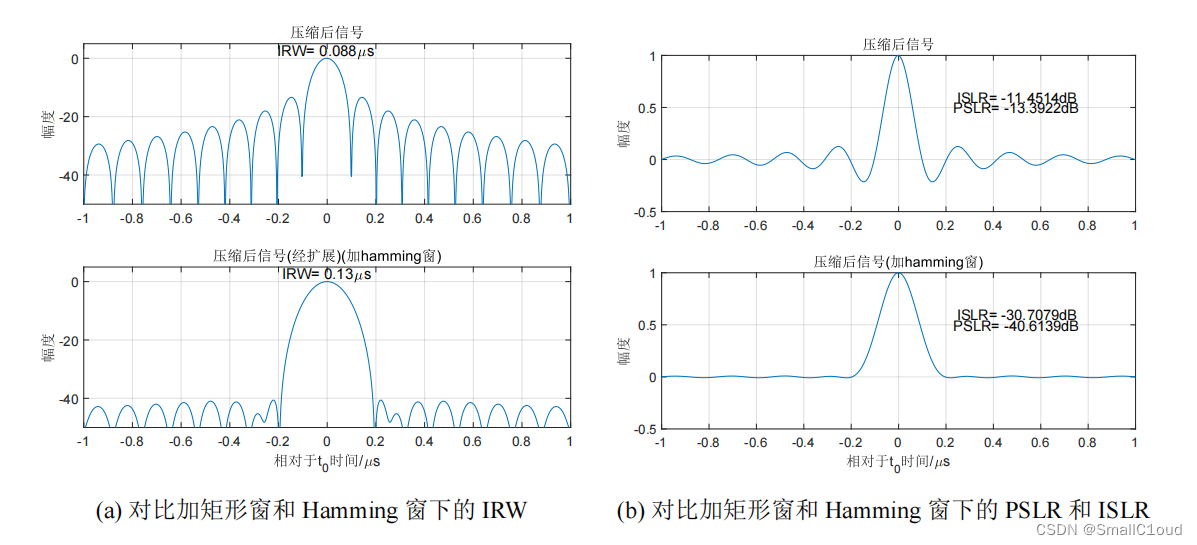
在这里插入图片描述

下图给出了矩形窗和加Hamming窗的脉冲压缩结果，Hamming又称改进版的升余弦窗，与矩形窗相比，Hamming窗将PSLR降低至-40.61dB，有效地抑制了副瓣的幅度，其幅度比加Hanning窗时要更低；ISLR降低至-30.71dB，使得能量集中在主瓣当中；分辨率扩展了1.48倍，一定程度上降低了分辨能力。总的来说，使用Hamming窗进行频域加窗处理可以改善脉冲压缩的副瓣抑制效果，但会导致脉冲宽度的增加(即分辨率降低)。

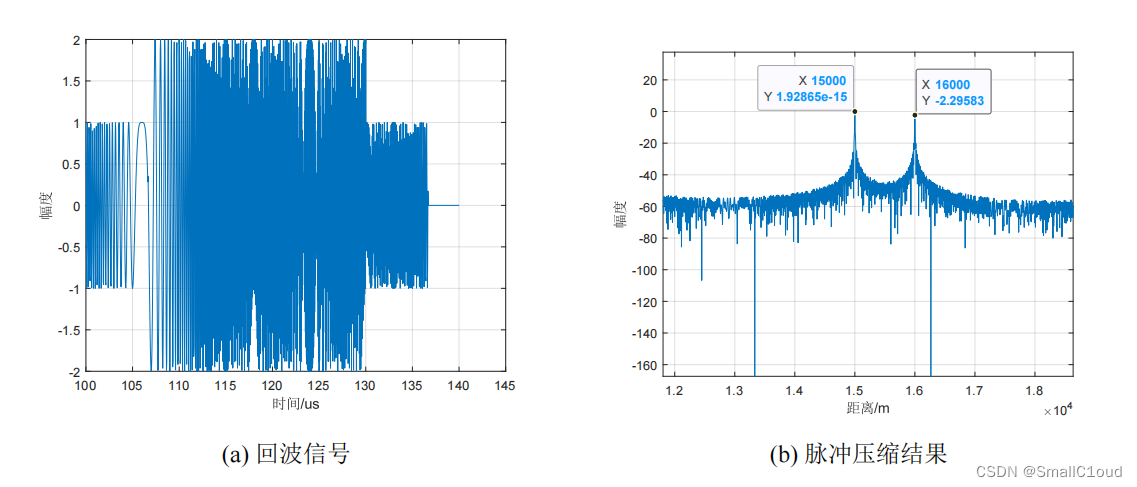
在这里插入图片描述