目录
1、泊松分布
2、卡方分布
3、正态分布
4、t分布
5、F分布
1、泊松分布
泊松分布是一种离散概率分布,描述了在固定时间或空间范围内,某个事件发生的次数的概率分布。该分布以法国数学家西蒙·德尼·泊松的名字命名,他在19世纪早期对这种分布进行了研究。
泊松分布的概率函数为:
P(X=k) = e^(-λ) * λ^k / k!
其中,P(X=k)表示事件发生k次的概率,λ是单位时间或单位空间内事件发生的平均次数。
泊松分布在各种自然和社会科学领域中都有广泛的应用,例如:
物理学:放射性衰变、粒子碰撞等随机过程。
生物学:动植物繁殖、遗传学等。
社会科学:人口统计、选举结果等。
经济学:金融市场波动、风险评估等。
此外,泊松分布与二项分布、指数分布和正态分布等其他概率分布有一定的关系。在统计分析中,泊松分布在处理具有固定时长或空间范围内的事件发生次数的问题时非常有用。
例如,如果你想计算在给定时间段内发生特定事件的概率,可以使用泊松分布。假设你有一个平均每小时发生10次的事件,你想知道在一小时内发生5次的概率。你可以使用Python的NumPy库来计算这个概率:
from scipy.stats import poisson# 平均每小时发生的事件次数lambda_value = 10# 想要计算的概率值k_value = 5# 使用泊松分布计算概率probability = poisson.pmf(k_value, lambda_value)print("在1小时内发生 {} 次事件的概率为: {}".format(k_value, probability))
在1小时内发生 5 次事件的概率为: 0.03783327480207079
生成泊松分布随机数
import numpy as np# 设定λ值,即事件的平均发生次数lambda_value = 10# 生成一个泊松分布的随机数poisson_random = np.random.poisson(lambda_value, 10000)# 打印结果print(poisson_random)
[ 6 5 9 ... 8 10 20]
2、卡方分布
卡方分布是概率统计中的一种重要分布,尤其在统计学中具有重要意义。它是通过正态分布构造而成的一个新的分布,当自由度n很大时,卡方分布近似为正态分布。
卡方分布的定义涉及到了多个相互独立的随机变量,这些随机变量都服从标准正态分布。当这些随机变量的平方和构成一新的随机变量时,其分布规律就是卡方分布。卡方分布的参数称为自由度,记为或者 (其中 , 为限制条件数)。自由度指包含的独立变量的个数。
卡方分布在数理统计中具有广泛应用。分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数的增大,分布趋近于正态分布。另外,分布的均值与方差也可以看出,随着自由度的增大,χ2分布向正无穷方向延伸(因为均值越来越大),分布曲线也越来越低阔(因为方差越来越大)。
卡方分布概率密度图像
import numpy as npimport matplotlib.pyplot as pltfrom scipy.stats import chi2# 设定自由度degrees_of_freedom = [2, 3, 4, 6, 9]# 设定x轴范围x = np.linspace(0, 20, 1000)# 对每一个自由度,计算卡方分布的概率密度函数for df in degrees_of_freedom:y = chi2.pdf(x, df)plt.plot(x, y, label=f'df={df}')# 设定图例、标题和轴标签plt.legend()plt.title('Chi-Squared Distribution')plt.xlabel('Value')plt.ylabel('Probability Density')# 显示图像plt.show()

计算卡方统计量和自由度,以及p值
import numpy as npfrom scipy import stats# 设定观察频数observed = np.array([[10, 10, 20], [20, 20, 20]])# 计算卡方统计量和自由度chi2, p, dof, expected = stats.chi2_contingency(observed)# 输出结果print("卡方统计量:", chi2)print("p值:", p)print("自由度:", dof)print("期望频数:", expected)
卡方统计量:2.7777777777777777
p值:0.2493522087772962
自由度:2
期望频数:[[12. 12. 16.]
[18. 18. 24.]]
3、正态分布
正态分布(Normal Distribution)是一种在数学、统计学和许多其他领域中广泛应用的概率分布。它以德国数学家卡尔·高斯(Carl Friedrich Gauss)命名,以描述在重复实验中测量值的概率分布。
正态分布的基本特征是概率密度函数呈钟形曲线,平均值为零,标准差恒定。该分布描述了在给定范围内的随机变量取值的概率,以及其最大可能的值和最小可能的值。
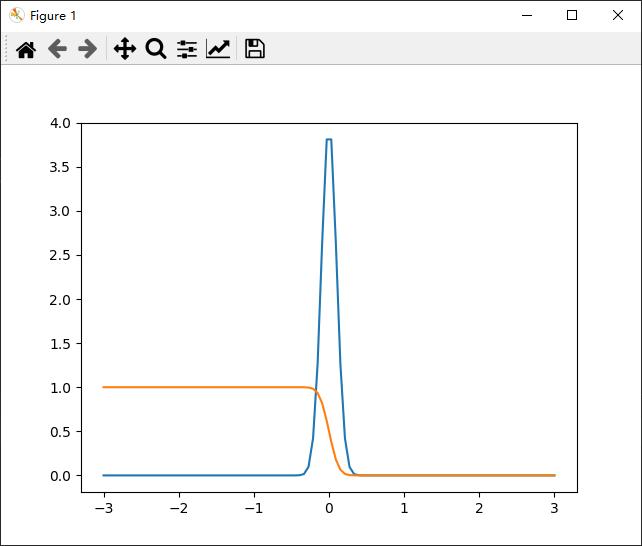
import numpy as npimport scipy.stats as stats# 均值和标准差mu, sigma = 0, 0.1 # 可以根据需要更改这些值# 计算正态分布的PDF和CDFpdf = stats.norm.pdf(x=np.linspace(-3, 3, 100), loc=mu, scale=sigma)cdf = stats.norm.cdf(x=np.linspace(-3, 3, 100), loc=mu, scale=sigma)# 输出PDF和CDF图像import matplotlib.pyplot as pltplt.plot(np.linspace(-3, 3, 100), pdf)plt.plot(np.linspace(-3, 3, 100), 1 - cdf)plt.show()
4、t分布
t分布(又称为学生t分布)是统计学上常用的概率分布之一,其定义是在给定样本量较小(小于30)或总体标准差未知的情况下,用来估计总体均值的分布。它由自由度(df)参数所决定。
t分布与正态分布类似,但是相比于正态分布而言,它的曲线形态稍微宽一些,也更加平坦。它的形状由自由度来决定,当自由度越大时,t分布逐渐趋近于正态分布。
from scipy.stats import t# 设置自由度df = 10# 计算x的概率密度函数值x = 2.5pdf = t.pdf(x, df)print("概率密度函数值:", pdf)# 计算小于等于x的累积分布函数值cdf = t.cdf(x, df)print("累积分布函数值:", cdf)
概率密度函数值: 0.026938727628244466
累积分布函数值: 0.9842765778816956
from scipy.stats import timport numpy as np# 设置自由度和生成随机数个数df = 10num_samples = 1000# 生成t分布的随机数样本samples = t.rvs(df, size=num_samples)# 输出前10个样本print("前10个样本:", samples[:10])# 计算样本均值和样本标准差mean = np.mean(samples)std = np.std(samples)print("样本均值:", mean)print("样本标准差:", std)
前10个样本: [ 1.03770461 0.81247149 -1.6061988 -0.10953492 -0.25427303 -0.50561028
-0.95062628 2.80638487 -0.29048675 -0.83396947]
样本均值: -0.013243567307352029
样本标准差: 1.104253454000021
5、F分布
F分布是统计学中常用的概率分布之一,用于比较两个样本方差的大小。它由两个自由度参数决定,分别称为分子自由度(df1)和分母自由度(df2)。
F分布的形状取决于分子自由度和分母自由度的值。当这两个自由度都大于1时,F分布呈现右偏斜的正态分布图形。F分布的区间在零点附近北向无限延伸,使得其概率密度函数的尾部比正态分布来得更长。F 分布总是非负的。
F 分布主要用于进行方差分析(ANOVA)和回归分析中的显著性检验。通过计算F 统计量,我们可以判断样本方差是否明显地不同,从而对比不同组之间的差异是否具有统计显著性。根据所得到的F值和相应的自由度,我们可以查找F分布表以计算p值来判断差异是否显著。
在Python中,你可以使用scipy.stats模块来计算 F 分布的概率密度函数(PDF)、累积分布函数(CDF),以及生成 F 分布的随机数样本。下面是一个示例代码:
from scipy.stats import f# 设置分子自由度和分母自由度df1 = 10df2 = 15# 计算x的概率密度函数值x = 2.5pdf = f.pdf(x, dfn=df1, dfd=df2)print("概率密度函数值:", pdf)# 计算小于等于x的累积分布函数值cdf = f.cdf(x, dfn=df1, dfd=df2)print("累积分布函数值:", cdf)# 生成F分布的随机数样本num_samples = 1000samples = f.rvs(dfn=df1, dfd=df2, size=num_samples)# 输出前10个样本print("前10个样本:", samples[:10])
概率密度函数值: 0.0742291142180768
累积分布函数值: 0.946860485660113
前10个样本: [0.92056996 1.87552153 0.75297048 2.69169927 0.31265751 0.63815811
1.08650558 0.7568914 0.63633434 1.14716638]