题目1:509 斐波那契数列
题目链接:斐波那契数列
对题目的理解
斐波那契数列由0和1开始,后面每一项数字(F(n))都是前两个数字的和,给一个n,计算F(n),(0<=n<=30)
动规五部曲
1)确定dp数组以及下标含义
dp[i]:第i个斐波那契数的数值 i:第i个斐波那契数
2)递推公式
dp[i] = dp[i-1] + dp[i-2]
3)dp数组初始化
dp[0] = 0
dp[1] = 1
4) 确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历
5)打印dp数组(debug)
伪代码

代码
class Solution {
public:int fib(int n) {if(n<=1) return n;vector<int> dp(n+1);dp[0] = 0;dp[1] = 1;for(int i=2;i<=n;i++){dp[i] = dp[i-1] + dp[i-2];}return dp[n];}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
压缩版本(优化空间复杂度)
也可以发现,不使用dp数组,只维护3个数值也可以求解,最终的dp[1]是所求,sum也是所求
伪代码

代码
class Solution {
public:int fib(int n) {if(n<=1) return n;int dp[2];dp[0] = 0;dp[1] = 1;int sum= 0;for(int i=2;i<=n;i++){//控制循环的次数,计算多少次sum = dp[0]+dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];//return sum;}
};注意:如果代码写成这样,就会报错未定义变量sum
报的错误如下
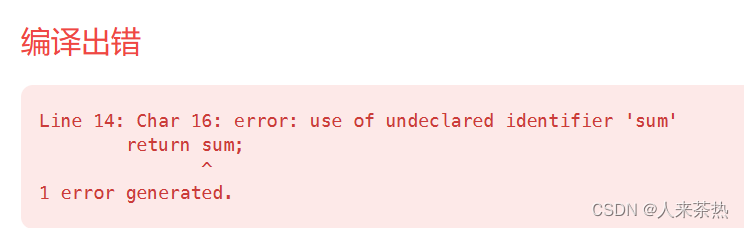
错误的原因是
sum只在循环内可用,出了循环就无法访问了。需要将 sum 定义在循环外面,这样才能在函数末尾返回。
所以将代码修改为如下
class Solution {
public:int fib(int n) {if(n<=1) return n;int dp[2];dp[0] = 0;dp[1] = 1;int sum= 0;for(int i=2;i<=n;i++){//控制循环的次数,计算多少次sum = dp[0]+dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];//return sum;}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
递归法
class Solution {
public:int fib(int n) {if(n<=1) return n;return fib(n-1)+fib(n-2);}
};- 时间复杂度:O(2^n)
- 空间复杂度:O(n),算上了编程语言中实现递归的系统栈所占空间
题目2:70 爬楼梯
题目链接:爬楼梯
对题目的理解
楼梯爬n阶才能到达楼顶,每次可以爬1或2个台阶,有多少种不同的爬法(1<=n<=45)
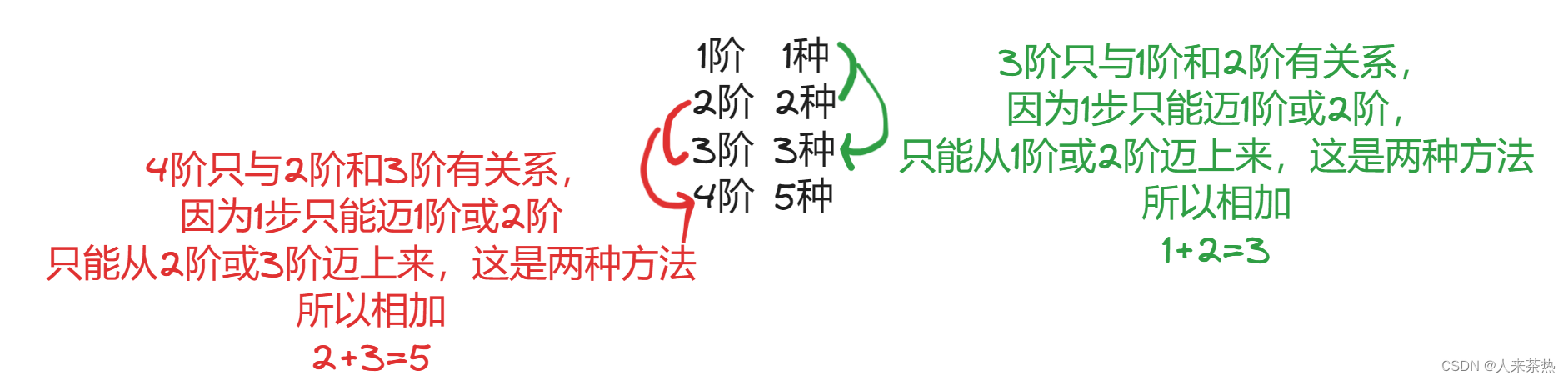
本题其实就是求斐波那契数列
动规五部曲
1)确定dp数组以及下标i的含义
dp[i]:达到第i阶有dp[i]种方法
2)确定递推公式
dp[i-1]再走1步到达dp[i] dp[i-2]再走2步到达dp[i]
dp[i]=dp[i-1]+dp[i-2]
3)初始化递归数组
dp[0]=1;//达到第0阶有1种方法,含义上说不通,因为题目的n>=1,因此,初始化dp[0]没有意义
dp[0]=0;//没有走,没有用方法,这个可以,但是初始化dp[0]没有意义
只初始化dp[1]和dp[2],dp[1]=1,dp[2]=2,达到第1阶有1种方法,达到第2种有两种方法
4)确定遍历顺序
从前向后遍历,dp[i]依赖于前两个状态dp[i-1]和dp[i-2].
5)打印dp数组
代码
class Solution {
public:int climbStairs(int n) {if(n<=2) return n;vector<int> dp(n+1);dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
压缩版本(优化空间复杂度)
直接维护3个数即可
class Solution {
public:int climbStairs(int n) {if(n<=2) return n;int dp[3];dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){int sum = dp[1]+dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
扩展
本题还可以扩展,比如一步一个台阶,两个台阶,三个台阶,直到m个台阶,有多少种方法爬到n阶楼顶,这时,此题变成了一个完全背包问题
题目链接:扩展楼梯(完全背包)
题目3:746 使用最小花费爬楼梯
题目链接:使用最小花费爬楼梯
对题目的理解
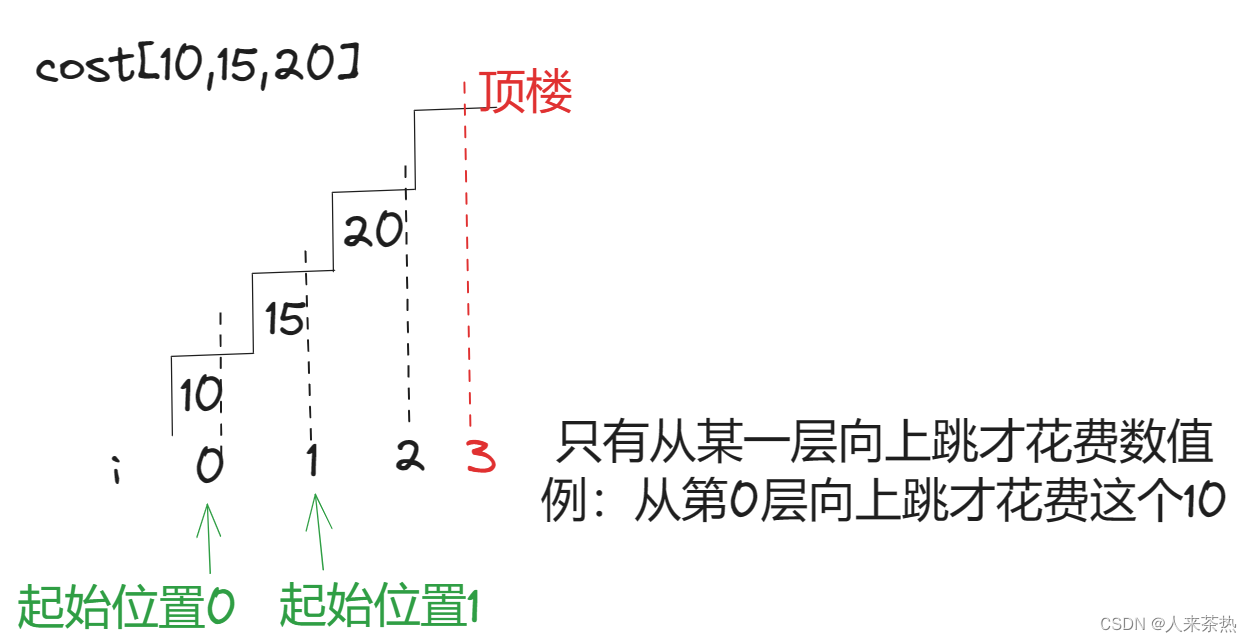
整数数组cost中的元素cost[i]从楼梯第i个台阶向上爬需要支付的费用,每次只能爬一个或者两个台阶,可以选择,从下标为0或下标为1的台阶开始爬
返回到达楼顶的最低花费
!!!注意楼顶的位置是cost.size()
动规五部曲
1)确定dp数组的含义以及下标i的含义
dp[i]表示到达第i个台阶(第i个位置)所需要的最小花费是dp[i]
2)递推公式
可以从i-1往上跳1步到达i,此时dp[i] = dp[i-1]+cost[i-1],两者相加是因为从底层跳到i-1层还需要dp[i-1]的花费,然后从i-1跳到i,还需要cost[i-1]的花费
也可以从i-2往上跳2步到达i,此时dp[i] = dp[i-2]+cost[i-2],两者相加是因为从底层跳到i-2层还需要dp[i-2]的花费,然后从i-2跳到i,还需要cost[i-2]的花费
因此,递推公式为dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2])
3)dp数组初始化
dp[0] = 0,因为题目中说可以从下标为0的台阶开始爬,所需最小花费是0
dp[1] = 0,因为题目中说可以从下标为1的台阶开始爬,所需最小花费是0
4)遍历顺序
从前向后遍历,因为dp[i]由dp[i-1]dp[i-2]推出
5)打印dp数组(debug)
代码
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+1);//初始化dp数组dp[0]=0;dp[1]=0;for(int i=2;i<=cost.size();i++){dp[i] = min(dp[i-1]+cost[i-1], dp[i-2]+cost[i-2]);}return dp[cost.size()];}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
压缩版本(优化空间复杂度)
不使用dp数组了,直接使用3个数值即可(有点绕)
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int dp[2];//初始化dp[0]=0;dp[1]=0;for(int i=2;i<=cost.size();i++){int minvalue = min(dp[1]+cost[i-1], dp[0]+cost[i-2]);dp[0] = dp[1];dp[1] = minvalue;}return dp[1];}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)