noip 2025.2.22

T3

题目大意：

给你一棵树和一个排列 \(p\)，定义 \(l \sim r\) 的 \(val\) 值为 \(dep_{LCA(p_{l \sim r})}\)，求

\[\sum_{i = 1}^n \sum_{j=i}^n val_{l, r} \]

\(n \le 6 \times 10^5\)

赛时思路：

先将 p 给直接映射上去。
考虑 \(\text{dsu on tree}\)，用 set 维护每个子树中一整段的标号，暴力合并。
时间复杂度：\(O(n \log^2n)\)，常数太大，无法通过。

solution A：

和 NOIP2024 T4 一样的结论。
考虑 \(dep_{LCA(l \sim r)}\) 能变成什么。
通过简单证明/虚树建树可知，他等于

\[\min_{k = l}^{r-1} dep_{LCA(l, l + 1)} \]

就是当一个点是 \(LCA\) 时，一定至少有两个儿子子树内包含这个区间的点，类似这样：

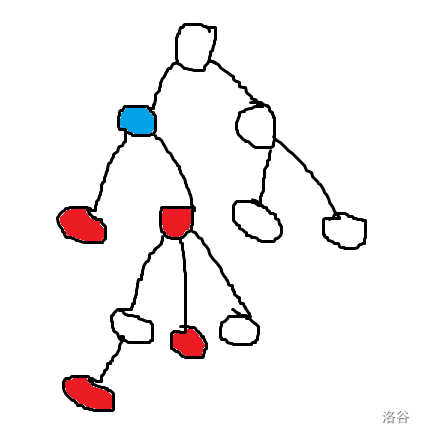
并且显然有

\[dep_{LCA(l,r)} \ge dep_{LCA(l \sim r + 1)} \]

就能得到这个结论。
那么求出相邻两个点的 \(LCA\)，就能变成求：

\[\sum_{i=1}^{n-1} \sum_{j = i}^{n-1} min_{k = i}^j dep_{LCA_{k,k+1}} \]

那么拿笛卡尔树做一下即可。

solution B：

还是 \(\text{dsu on tree}\)，但这次是拿并查集。
顺序是先递归轻儿子，然后清空轻儿子的修改，再次递归重儿子，将结果保留。
所以也是 \(O(n \log^2 n)\) 的，但是常数很小。
也可以优化成 \(O(n \log n \ \alpha n)\) 的。
挺套路的，不过也挺快的。

T4：

题目大意：

给定一张无向图，每条边有断开的概率，问期望的连通块个数。
\(n \le 17\)。
空间 256MB，开不下 \(3^n\) 的数组。

赛时思路：

设 \(f_{S}\) 表示集合 \(S\) 中期望联通块个数。
然后转移就是枚举一个联通块，为了避免算重，强定他包含 \(lowbit(S)\)。
直接转移不了。

然后再设 \(h_{S}\) 表示集合 \(S\) 为一个联通块的概率。
考虑容斥，用 1 减去不合法的方案。
那么枚举 \(lowbit(S)\) 所在的连通块。

发现由于 \(f,h\) 目前都无法转移，因为枚举的连通块要保证与外面的点无边。
所以设 \(g_{i, S}\) 表示 \(i\) 与 \(S\) 中每个点都断开的概率。

那么预处理出 g，就可以 \(O(n)\) 地给 \(h,f\) 转移了。
但过不去，只能过 \(n \le 15\)。

解题思路：

考虑优化转移 \(f,h\) 的时间复杂度。
由于要求的是给定两个集合 \(S,T\)，求 \(S,T\) 之间无边的概率。
那么就可以抽象成这样的图：

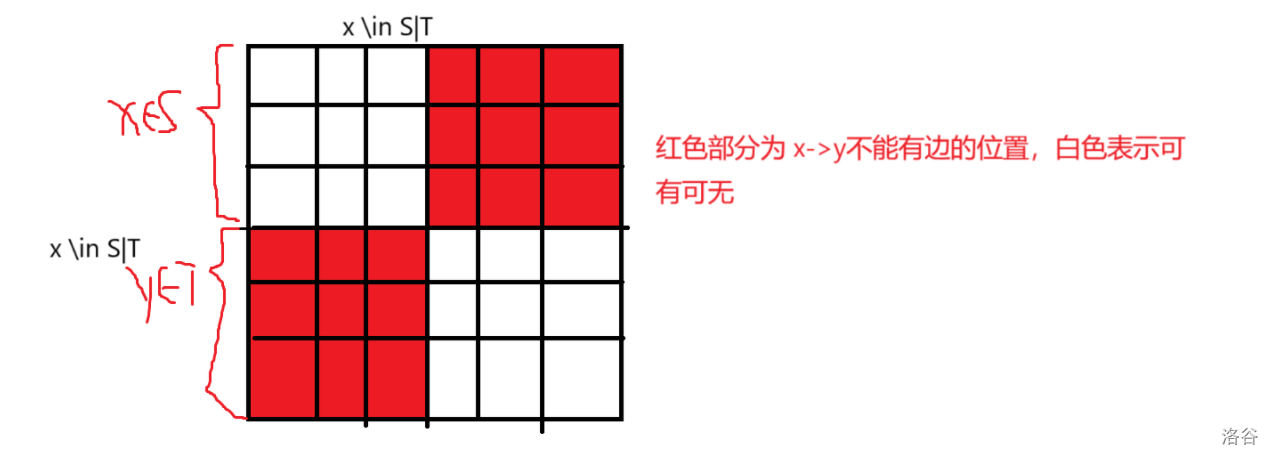
那么设 \(dp_{S}\) 表示集合 \(S\) 内不许有边的概率。
那么上面 \(f,h\) 的 \(O(n)\) 转移就可变成 \(O(1)\) 的。
就是 \(\frac{dp_{S|T}}{dp_{S} \times dp_{T}}\)。
那么就可以 \(O(3^n)\) 了。