04、基于高斯分布的异常检测算法-编程知识

04、基于高斯分布的异常检测算法原理与实践

开始学习机器学习啦，已经把吴恩达的课全部刷完了，现在开始熟悉一下复现代码。对这个手写数字实部比较感兴趣，作为入门的素材非常合适。

数据的严重偏斜往往会导致监督学习算法面临巨大的挑战——尤其是在负样本数量稀缺的情况下，监督学习模型难以充分汲取必要的知识。这就引发了一个重要的问题：我们能否从这种极端不平衡的数据中成功地训练出一个有效的异常检测模型呢？答案就在于基于统计学的异常检测算法。

此类方法通常建立在一种假设之上，即给定的数据集遵循某种随机分布模型，任何与该模型明显不符的样本都会被视为异常样本。在这些基于统计学的异常检测算法中**，高斯模型是最常用分布模型**。

当然，如果给定的原始数据集不遵循高斯分布，我们可以通过坐标轴变换的方式将其变换为符合高斯分布的数据再进行异常检测。

1、基于高斯分布的异常检测算法原理

高斯分布的概率密度函数如下所示：
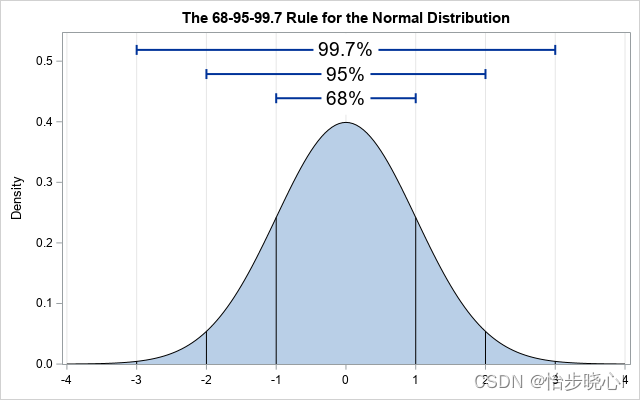
在这里插入图片描述
处于图片的中心位置，是概率密度最高的地方，这代表此种情况是经常发生的。越向两边概率密度越低，这代表这些情况较小发生，更有可能是异常情况。我们需要的是确定这个阈值，当概率密度小于多少时则认定其为异常。

这种基于高斯分布的异常检测算法在训练时不需要标签，只需要根据训练数据计算出各个特征的均值与方差即可（就是高斯分布的参数）。在训练之后，可以根据少量的数据确定异常的阈值，从而实现整个异常检测算法。

对于高维的异常检测算法，其理论是一致的，如下面的二维概率密度的等高线图，处于边缘的会往往会被视为异常情况（小概率出现的事件）：
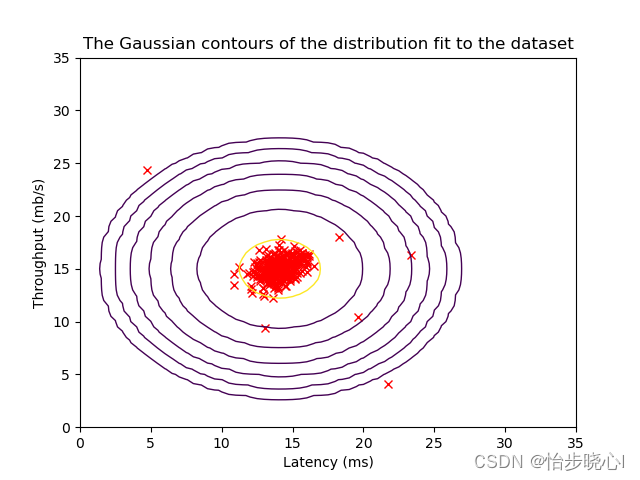
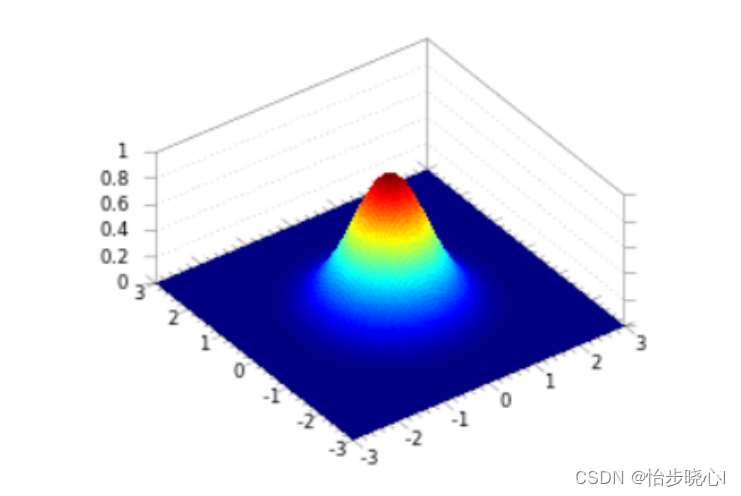
在这里插入图片描述

至于为什么小概率事件会等同于异常呢，打个比方，训练集得出结论人是吃米的，但是出来一个奇葩人居然吃虫子，那么这个不相当于出现异常了嘛。

2、基于高斯分布的异常检测算法实现

STEP1: 从训练集计算数据的分布特性，主要是均值和方差

# 计算数据的均值与方差
def estimate_gaussian(X):mu = np.mean(X, axis=0)var = np.var(X, axis=0)return mu, var

STEP2: 将交叉验证集应用到概率分布上，得到其分布概率

# 定义一个函数，名为multivariate_gaussian，输入参数为X（样本点）、mu（均值向量）和var（方差）
def multivariate_gaussian(X, mu, var):# 计算均值向量的长度，也即特征的数量k = len(mu)# 如果输入的协方差矩阵是一维的，则将其转换为对角矩阵if var.ndim == 1:var = np.diag(var)# 将输入的样本点X减去均值向量mu，进行中心化处理X = X - mu# 计算多元高斯分布的概率密度函数值# 公式中的各部分分别计算，最后相乘得到结果p = (2 * np.pi) ** (-k / 2) * np.linalg.det(var) ** (-0.5) * \np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))# 返回概率密度函数值return p

其对应的公式如下：
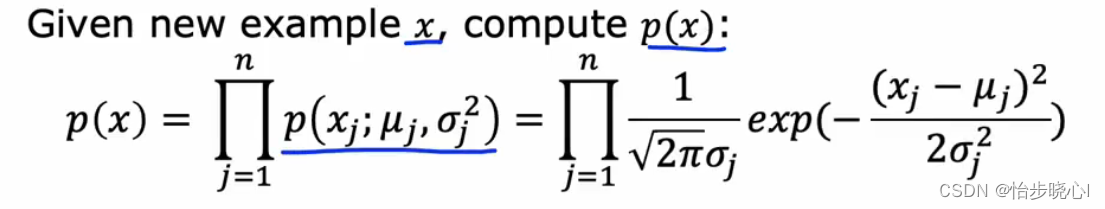
在这里插入图片描述

STEP3: 根据交叉验证集得出阈值

epsilon 的选择使用的是便利的方法，以找到一个使得F1 score最大的epsilon ：

def select_threshold(y_val, p_val):"""通过选择最佳的阈值来最大化F1分数。参数:y_val (numpy数组): 真实的标签值，1代表正类，0代表负类。p_val (numpy数组): 预测的概率值。返回:best_epsilon, best_F1: 包含最佳阈值和对应的最大F1分数。"""best_epsilon = 0  # 初始化最佳阈值为0best_F1 = 0  # 初始化最佳F1分数为0F1 = 0  # 当前的F1分数# 计算步长，使得在p_val的最小值和最大值之间有1000个步骤step_size = (max(p_val) - min(p_val)) / 1000# 对p_val中的每一个值进行遍历，从最小值到最大值，步长为step_sizefor epsilon in np.arange(min(p_val), max(p_val), step_size):# 根据当前的阈值epsilon，得到预测的标签predictions = (p_val < epsilon)# 计算假阳性（预测为正但实际为负的样本数）fp = sum((predictions == 1) & (y_val == 0))# 计算真阳性（预测为正且实际为正的样本数）tp = np.sum((predictions == 1) & (y_val == 1))# 计算假阴性（预测为负但实际为正的样本数）fn = np.sum((predictions == 0) & (y_val == 1))# 计算精确度（查准率）prec = tp / (tp + fp)# 计算召回率（查全率）rec = tp / (tp + fn)# 计算F1分数F1 = 2 * prec * rec / (prec + rec)# 如果当前的F1分数比之前的最佳F1分数还要大，则更新最佳F1分数和对应的阈值if F1 > best_F1:best_F1 = F1best_epsilon = epsilon# 返回最佳阈值和对应的最大F1分数return best_epsilon, best_F1

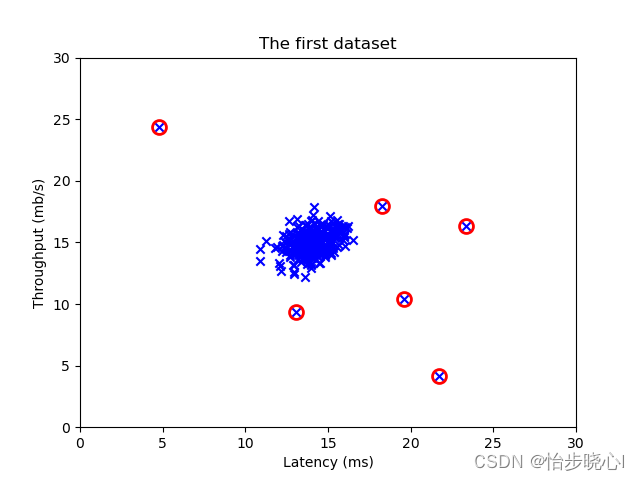
STEP4: 由此就可以根据交叉验证集得到的阈值计算训练集中的异常数据了
下面是结果：
在这里插入图片描述

3、完整代码

工程的下载链在最上方：

import numpy as np
import matplotlib.pyplot as pltdef load_data():X = np.load("Anomaly_Detection_data/X_part1.npy")X_val = np.load("Anomaly_Detection_data/X_val_part1.npy")y_val = np.load("Anomaly_Detection_data/y_val_part1.npy")return X, X_val, y_val
# 计算数据的均值与方差
def estimate_gaussian(X):mu = np.mean(X, axis=0)var = np.var(X, axis=0)return mu, var# 定义一个函数，名为multivariate_gaussian，输入参数为X（样本点）、mu（均值向量）和var（方差）
def multivariate_gaussian(X, mu, var):# 计算均值向量的长度，也即特征的数量k = len(mu)# 如果输入的协方差矩阵是一维的，则将其转换为对角矩阵if var.ndim == 1:var = np.diag(var)# 将输入的样本点X减去均值向量mu，进行中心化处理X = X - mu# 计算多元高斯分布的概率密度函数值# 公式中的各部分分别计算，最后相乘得到结果p = (2 * np.pi) ** (-k / 2) * np.linalg.det(var) ** (-0.5) * \np.exp(-0.5 * np.sum(np.matmul(X, np.linalg.pinv(var)) * X, axis=1))# 返回概率密度函数值return pdef visualize_fit(X, mu, var):# 首先画出等高线，坐标在0, 35.5之间X1, X2 = np.meshgrid(np.arange(0, 35.5, 0.5), np.arange(0, 35.5, 0.5))Z = multivariate_gaussian(np.stack([X1.ravel(), X2.ravel()], axis=1), mu, var)Z = Z.reshape(X1.shape)plt.plot(X[:, 0], X[:, 1], 'rx')if np.sum(np.isinf(Z)) == 0:plt.contour(X1, X2, Z, levels=10 ** (np.arange(-20., 1, 3)), linewidths=1)plt.title("The Gaussian contours of the distribution fit to the dataset")plt.ylabel('Throughput (mb/s)')plt.xlabel('Latency (ms)')plt.show()def select_threshold(y_val, p_val):"""通过选择最佳的阈值来最大化F1分数。参数:y_val (numpy数组): 真实的标签值，1代表正类，0代表负类。p_val (numpy数组): 预测的概率值。返回:best_epsilon, best_F1: 包含最佳阈值和对应的最大F1分数。"""best_epsilon = 0  # 初始化最佳阈值为0best_F1 = 0  # 初始化最佳F1分数为0F1 = 0  # 当前的F1分数# 计算步长，使得在p_val的最小值和最大值之间有1000个步骤step_size = (max(p_val) - min(p_val)) / 1000# 对p_val中的每一个值进行遍历，从最小值到最大值，步长为step_sizefor epsilon in np.arange(min(p_val), max(p_val), step_size):# 根据当前的阈值epsilon，得到预测的标签predictions = (p_val < epsilon)# 计算假阳性（预测为正但实际为负的样本数）fp = sum((predictions == 1) & (y_val == 0))# 计算真阳性（预测为正且实际为正的样本数）tp = np.sum((predictions == 1) & (y_val == 1))# 计算假阴性（预测为负但实际为正的样本数）fn = np.sum((predictions == 0) & (y_val == 1))# 计算精确度（查准率）prec = tp / (tp + fp)# 计算召回率（查全率）rec = tp / (tp + fn)# 计算F1分数F1 = 2 * prec * rec / (prec + rec)# 如果当前的F1分数比之前的最佳F1分数还要大，则更新最佳F1分数和对应的阈值if F1 > best_F1:best_F1 = F1best_epsilon = epsilon# 返回最佳阈值和对应的最大F1分数return best_epsilon, best_F1# Load the dataset
# 利用吞吐量（兆比特/秒）和每台服务器的响应延迟（毫秒）来判断服务器是否正常运行
X_train, X_val, y_val = load_data()
print ('The shape of X_train is:', X_train.shape)
print ('The shape of X_val is:', X_val.shape)
print ('The shape of y_val is: ', y_val.shape)# Estimate mean and variance of each feature
# 一共两个特征，因此返回的是一个包含两个元素的数组
mu, var = estimate_gaussian(X_train)
visualize_fit(X_val, mu, var)
p_val = multivariate_gaussian(X_val, mu, var)
p = multivariate_gaussian(X_train, mu, var)
epsilon, F1 = select_threshold(y_val, p_val)# Find the outliers in the training set
outliers = p < epsilon
# Visualize the fit
visualize_fit(X_train, mu, var)
# 查看训练数据
plt.scatter(X_train[:, 0], X_train[:, 1], marker='x', c='b')
plt.title("The first dataset")
plt.ylabel('Throughput (mb/s)')
plt.xlabel('Latency (ms)')
plt.axis([0, 30, 0, 30])
# Draw a red circle around those outliers
plt.plot(X_train[outliers, 0], X_train[outliers, 1], 'ro',markersize= 10,markerfacecolor='none', markeredgewidth=2)
plt.show()