简单选择排序
基本思想
非常基础的算法,假设有N个数据,比较N-1轮,每轮选出当前剩余数据的最大(最小)放到数据
的开头,之后重复即可获得答案。
示例
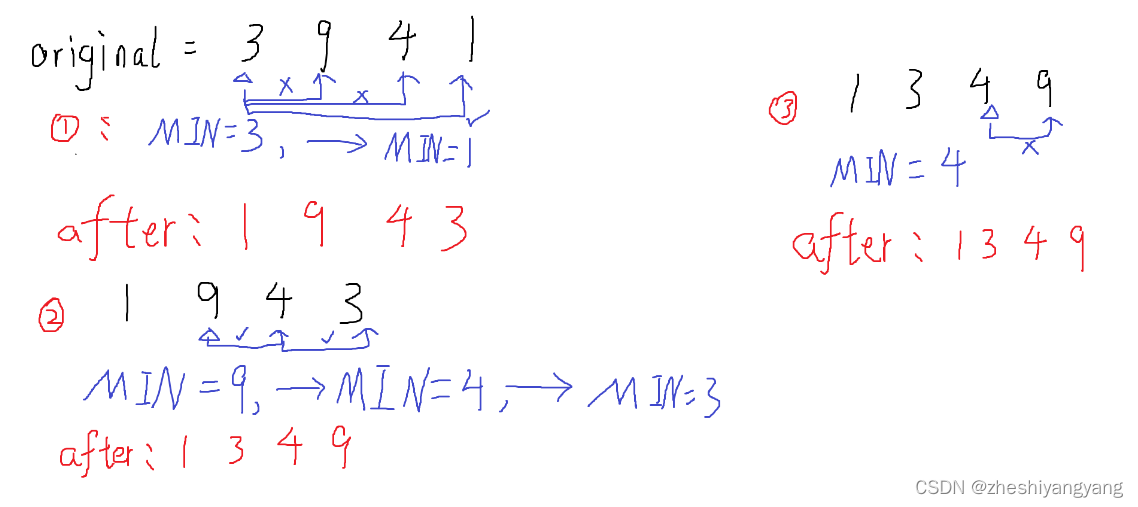
代码
void SelectSort(OrderList *L)
{RecordType tmp;int i,j,min;for(i=1;i<=L->length-1;i++){min = i;for(j=i+1;j<=L->length;j++){if(L->data[j].key < L->data[min].key){min = j;}}if(min!=i){tmp = L->data[min];L->data[min] = L->data[i];L->data[i] = tmp;}}
}堆排序
堆的概念
若有n个记录组成的序列{n1,n2,n3,.....n}
满足如下关系的时候,称作“堆”:

若将该序列换为完全二叉树,则我们可以得到一个:“非终端结点的值均小于其左右孩子,即根节
点最小”,这种特征的一个完全二叉树。
因此,若序列是堆,那么堆顶元素(完全二叉树的根节点)必定是这n个元素中的最小值。
基本思想
1.我们需要先将一个无序序列排成一个:“小根堆”。(所有非终端结点均小于其左右孩子)。
我们还知道一颗完全二叉树的非终端结点的最后一个节点的序号一定为[n/2](向下取整)。
因此,我们可以先对前[n/2]个结点依次进行根排序,就可以得到一个:“小根堆”。
2.此时我们将堆顶元素根堆底元素交换,再将堆顶元素进行堆排序,再把排序后的堆顶元素与堆底
元素交换。如此重复,直到只剩余一个元素没有进行顶底交换为止。
代码
void HeapAdjust(OrderList *L,int m,int n) //堆排序
{ //在函数中,默认m结点是没有堆排序的,但是[m+1,n]结点已经堆排序 RecordType tmp;int i;tmp = L->data[m];for(i=2*m;i<=n;i*=2){ //每次乘2,因为仿照完全二叉树 if(i<n&&L->data[i].key>L->data[i+1].key) //i永远存储统一左右孩子中较小的孩子索引 i++;if(tmp.key<L->data[i].key) //tmp小于最小的孩子,说明排序完成 break;L->data[m] = L->data[i]; //交换当前层次的最小结点 m = i; //m是i的父节点 }L->data[m] = tmp; //成功交换
}void HeapSort(OrderList *L) //堆顶与堆底元素交换(元素输出)
{RecordType tmp;int i;for(i=L->length/2;i>0;i--) //对前[n/2]非终端结点进行堆排序,形成一个"小根堆" HeapAdjust(L,i,L->length);for(i=L->length;i>1;i--){ //堆顶与堆底结点交换 tmp = L->data[1];L->data[1] = L->data[i];L->data[i] = tmp;HeapAdjust(L,1,i-1); //重新对剩余的结点进行堆排序 }
}
总代码
#include<stdio.h>
#define MAX 100
typedef int KeyType;
typedef struct{KeyType key;
}RecordType;
typedef struct{RecordType data[MAX];int length;
}OrderList;void SelectSort(OrderList *L)
{RecordType tmp;int i,j,min;for(i=1;i<=L->length-1;i++){min = i;for(j=i+1;j<=L->length;j++){if(L->data[j].key < L->data[min].key){min = j;}}if(min!=i){tmp = L->data[min];L->data[min] = L->data[i];L->data[i] = tmp;}}
}void HeapAdjust(OrderList *L,int m,int n) //堆排序
{ //在函数中,默认m结点是没有堆排序的,但是[m+1,n]结点已经堆排序 RecordType tmp;int i;tmp = L->data[m];for(i=2*m;i<=n;i*=2){ //每次乘2,因为仿照完全二叉树 if(i<n&&L->data[i].key>L->data[i+1].key) //i永远存储统一左右孩子中较小的孩子索引 i++;if(tmp.key<L->data[i].key) //tmp小于最小的孩子,说明排序完成 break;L->data[m] = L->data[i]; //交换当前层次的最小结点 m = i; //m是i的父节点 }L->data[m] = tmp; //成功交换
}void HeapSort(OrderList *L) //堆顶与堆底元素交换(元素输出)
{RecordType tmp;int i;for(i=L->length/2;i>0;i--) //对前[n/2]非终端结点进行堆排序,形成一个"小根堆" HeapAdjust(L,i,L->length);for(i=L->length;i>1;i--){ //堆顶与堆底结点交换 tmp = L->data[1];L->data[1] = L->data[i];L->data[i] = tmp;HeapAdjust(L,1,i-1); //重新对剩余的结点进行堆排序 }
}int main()
{int sample[11]={0,6,9,11,2,100,66,55,9,101,1000};int i;OrderList L;L.length = 10;for(i=1;i<=L.length;i++)L.data[i].key = sample[i];//SelectSort(&L);//HeapSort(&L);for(i=1;i<=L.length;i++)printf("%d ",L.data[i].key);return 0;
}