数据结构 -- 并查集与图

目录

1.并查集

1.结构

2.原理

3.代码实现

1.存储

2.寻找根节点

3.是否为同一集合

4.求集合个数

5.合并为同一集合中

整体代码

2.图

1.基本知识

1.各个属性

2.特殊名词

3.图的解释

2.图的表示

1.邻接矩阵

2.邻接表

3.图的遍历

1.BFS--广度优先遍历

2.DFS--深度优先遍历

1.并查集

定义:n个元素被划分在不相交的集合中,一旦出现某几个元素可以形成一个相同的集合内,那么此时就会被该结构放入同一个集合内.该集合的好处就是当需要查询就能得到某个元素是属于哪个集合中.

1.结构

其实无非就是用于记载是否存在在哪个集合中,那么只需要有一个能存储某个位置对应的集合,而位置是唯一的,那么每一个位置其实就已经代表特定的元素.

1.为了表示存储元素的位置,那么就需要一个vector

2.每个位置对应的元素,那么只需要hash表即可表示特定的元素的特定下标

2.原理

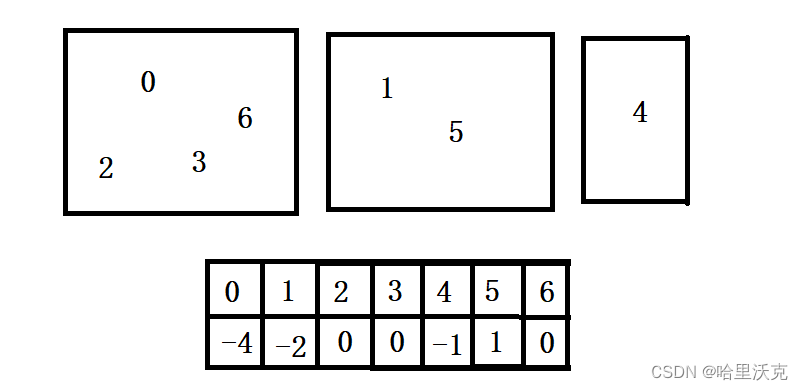
1.其实我们可以把并查集表示为森林

2.如果下标对应的元素为正数,则表示和元素对应下标的元素为同一集合;如果下标对应的元素为负数,表示当前为森林的顶端

3.如果我们已经知道每个下标代表的意义,那么不需要哈希表进行表示.如果需要对下标进行解析,可以使用hash对元素和下标进行映射

3.代码实现

1.存储

class UnionFindSet
{
private:vector<int> _ufs;
public:UnionFindSet(size_t n):_ufs(n, -1){}
}

1.先设置一个vector

2.构造时,需要多少元素就设置多少,并且初始化为-1,表示当前的元素独立

2.寻找根节点

int FindRoot(int x)
{int root = x;while (_ufs[root] >= 0)root = _ufs[root];while (_ufs[x] >= 0){int parent = _ufs[x];_ufs[x] = root;x = parent;}return root;
}

我们知道循着元素下标往上找就能找到我们需要的根节点并且实现压缩数据

3.是否为同一集合

bool InSet(int x1, int x2)
{return FindRoot(x1)== FindRoot(x2);
}

对比二者的根节点是否相同即可

4.求集合个数

size_t SetSize()
{size_t size = 0;for (size_t i = 0; i < _ufs.size(); i++){if (_ufs[i] < 0) size++;}return size;
}

只需要根节点就可以了,根节点的特点就是元素为负数,那么只需要遍历vector,计算负数的个数就可以了.

5.合并为同一集合中

void Uinon(int x1, int x2)
{int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2) return;if (abs(_ufs[root1]) < abs(_ufs[root2])) swap(root1, root2);_ufs[root1] += _ufs[root2];_ufs[root2] = root1;
}

1.找到两个元素对应的根节点,如果根节点相同则不需要结合

2.如果不相同,我们需要将数据量小的合并到数据量大的去

3.那么当前root1就是小的下标._ufs[root1] += _ufs[root2]表示当前的root1为根节点时的所有元素个数,_ufs[root2] = root1将root2的下标记作root1

整体代码

class UnionFindSet
{
private:vector<int> _ufs;
public:UnionFindSet(size_t n):_ufs(n, -1){}void Uinon(int x1, int x2){int root1 = FindRoot(x1);int root2 = FindRoot(x2);if (root1 == root2) return;if (abs(_ufs[root1]) < abs(_ufs[root2])) swap(root1, root2);_ufs[root1] += _ufs[root2];_ufs[root2] = root1;}int FindRoot(int x){int root = x;while (_ufs[root] >= 0)root = _ufs[root];while (_ufs[x] >= 0){int parent = _ufs[x];_ufs[x] = root;x = parent;}return root;}bool InSet(int x1, int x2){return FindRoot(x1)== FindRoot(x2);}size_t SetSize(){size_t size = 0;for (size_t i = 0; i < _ufs.size(); i++){if (_ufs[i] < 0) size++;}return size;}
};

2.图

1.基本知识

1.各个属性

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V，E)

1.顶点集合:V = {x|x属于某个数据对象集}是有穷非空集合
2.边集合:E = {(x,y)|x,y属于V}或者E={<x, y>|x,y属于V&&Path(x, y)}是顶点间关系的有穷集合.

3.图的种类可分为:有向图和无向图

2.特殊名词

1.完全图：每一个顶点都互相有一个边联通的叫完全图。[其中在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图；在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图]

2.邻接顶点：两个顶点通过一个边可互相抵达的。[在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联]

3.顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。[在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。注意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)]

4.路径：在图G = (V， E)中，两顶点可经过若干边抵达的,就叫路劲。若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。

5.路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和

3.图的解释

1.简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径;若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。
2.子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图
3.连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图

4.强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到vi的路径，则称此图是强连通图

5.生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n-1条边。

2.图的表示

1.邻接矩阵

1.适合存储非常稠密的图

2.邻接矩阵可以O(1)判断两个顶点之间的连接关系

3.一个点的所有边不方便找

namespace Matrix
{template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>class Graph{public://图的创建 -- 1.IO  2.关系放在文件中  3.手动添加边Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; ++i){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_matrix.resize(n);for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){_matrix.resize(n, MAX_W);}}}size_t GetVertexIndex(const V& v){auto it = _indexMap.find(v);if (it == _indexMap.end()){throw invalid_argument("顶点不存在");return -1;}else{return it->second;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){// 打印顶点和下标映射关系for (size_t i = 0; i < _vertexs.size(); ++i){cout << _vertexs[i] << "-" << i << " ";}cout << endl;cout << "  ";for (size_t i = 0; i < _matrix.size(); i++){cout << i << " ";for (size_t j = 0; j < _matrix[0].size(); j++){if (_matrix[i][j] == MAX_W)cout << "* ";elsecout << _matrix[i][j] << " ";}cout << endl;}cout << endl;}private:vector<V> _vertexs; //保存顶点map<V, int> _indexMap; //顶点与下标映射vector<vector<W>> _matrix; //邻接矩阵};
}

2.邻接表

1.适合比较稀疏的图

2.适合找到一个顶点的所有边

3.不适合判断两个顶点之间的连接关系

namespace link_table
{template<class W>struct Edge{int _dsti; //目标点下标W _w; //权值Edge<W>* _next;Edge(int dsti,const int w):_dsti(dsti),_w(w),_next(nullptr){}};template<class V, class W, bool Direction = false>class Graph{typedef Edge<W> Edge;public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; ++i){_vertexs.push_back(a[i]);_indexMap[a[i]] = i;}_table.resize(n, nullptr);}size_t GetVertexIndex(const V& v){auto it = _indexMap.find(v);if (it == _indexMap.end()){throw invalid_argument("顶点不存在");return -1;}else{return it->second;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetVertexIndex(src);size_t dsti = GetVertexIndex(dst);//srci->dstiEdge* eg = new Edge(dsti, w);eg->_next = _table[srci];_table[srci] = eg;//无向图 dsti->srciif (Direction == false){Edge* eg = new Edge(srci, w);eg->_next = _table[dsti];_table[dsti] = eg;}}void Print(){// 打印顶点和下标映射关系for (size_t i = 0; i < _vertexs.size(); ++i){cout << _vertexs[i] << "-" << i << " ";}cout << endl;for (size_t i = 0; i < _table.size(); i++){cout << _vertexs[i] << "[" << i << "]->";Edge* cur = _table[i];while (cur){cout << "{" << _vertexs[cur->_dsti] << "[" << cur->_dsti << "]" << cur->_w << "}->";cur = cur->_next;}cout << "{nullptr}" << endl;}}private:vector<V> _vertexs; //保存顶点map<V, int> _indexMap; //顶点与下标映射vector<Edge*> _table; //邻接表};
}

3.图的遍历

1.BFS--广度优先遍历

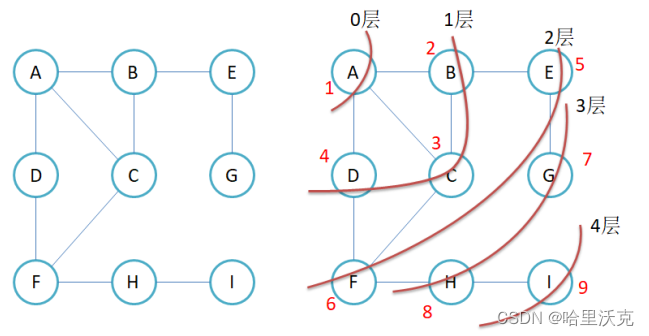
1.bfs的实现其实就是基于队列实现的

2.先将第一个顶点push到队列中,那么我们就可以基于该顶点进行遍历.需要注意的是,我们需要一个表来查看走到的点是否已经遍历过了

3.之后的循环,每次都查看每一层的顶点,并且将下一层的相邻顶点连接.遍历过的点pop掉并且将其访问的点进行标记已经访问

		void BFS(const V& src){size_t srci = GetVertexIndex(src);// 队列和标记数组queue<int> q;vector<bool> visited(_vertexs.size(), false);q.push(srci);visited[srci] = true;int levelSize = 1;size_t n = _vertexs.size();while (!q.empty()){// 一层一层出for (int i = 0; i < levelSize; ++i){int front = q.front();q.pop();cout << front << ":" << _vertexs[front] << " ";// 把front顶点的邻接顶点入队列for (size_t i = 0; i < n; ++i){if (_matrix[front][i] != MAX_W){if (visited[i] == false){q.push(i);visited[i] = true;}}}}cout << endl;levelSize = q.size();}cout << endl;}

2.DFS--深度优先遍历

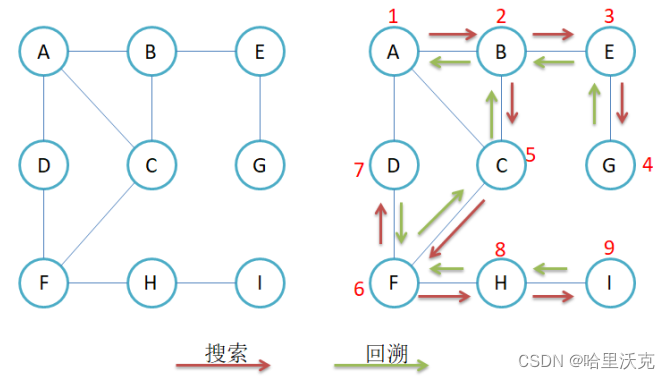
将当前访问的点进行遍历,随后标记为访问过了,循环该点的其他相邻点,同样的逻辑

		void _DFS(size_t srci, vector<bool>& visited){cout << srci << ":" << _vertexs[srci] << endl;visited[srci] = true;for (size_t i = 0; i < _vertexs.size(); ++i){if (_matrix[srci][i] != MAX_W && visited[i] == false){_DFS(i, visited);}}}void DFS(const V& src){size_t srci = GetVertexIndex(src);vector<bool> visited(_vertexs.size(), false);_DFS(srci, visited);}

这样的代码其实有弊端,就是只能遍历相邻的点.一旦该图不是连通图就会出现只能访问一部分.那么就需要在DFS处遍历每一个点,如果没有被_DFS遍历标记过就需要再一次进行_DFS遍历

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/230937.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

centos7中通过kubeadmin安装k8s集群

centos7中通过kubeadmin安装k8s集群

k8s部署官方提供了kind、minikube、kubeadmin等多种安装方式。 其中minikube安装在之前的文章中已经介绍过&#xff0c;部署比较简单。下面介绍通过kubeadmin部署k8s集群。 生产中提供了多种高可用方案&#xff1a; k8s官方文档 本文安装的是1.28.0版本。 建议去认真阅读一下…
阅读更多...
函数的极值与最值

函数的极值与最值

函数的最值 1.闭区间上连续函数的最值 1.求驻点或不可导点&#xff08;可能的极值点&#xff09; 2.求函数在驻点&#xff0c;不可导点&#xff0c;端点的函数值 3.比较大小 例题&#xff1a; 例题思想&#xff1a;分段函数分段点必须验证导数的存在性 几种常见的最值类型 1.…
阅读更多...
Vue3-Eslint配置代码风格

Vue3-Eslint配置代码风格

prettier风格配置 官网&#xff1a;https://prettier.io Eslint&#xff1a;代码纠错&#xff0c;关注于规范 prettier&#xff1a;专注于代码格式化的插件&#xff0c;让代码更加美观 两者各有所长&#xff0c;配合使用优化代码 生效前提&#xff1a; 1&#xff09;禁用…
阅读更多...
Langchain-Chatchat的安装过程

Langchain-Chatchat的安装过程

参考&#xff1a;LLMs之RAG&#xff1a;LangChain-Chatchat(一款中文友好的全流程本地知识库问答应用)的简介(支持 FastChat 接入的ChatGLM-2/LLaMA-2等多款主流LLMs多款embe_一个处女座的程序猿的博客-CSDN博客 1、安装过程中出现了 GPU驱动版本 是11.8 而 python -c "…
阅读更多...
Tomcat 修改版本号

Tomcat 修改版本号

lib 目录下增加文件 /lib/org/apache/catalina/util/ServerInfo.properties ServerInfo.properties文件里面只需要输入server.info显示的版本号 其他可配置信息 server.infonginx server.number22.0 server.builtMay 11 2023 08:22:10 UTC 显示效果
阅读更多...
低调使用。推荐一个 GPT4 Turbo、Vision、GPTs、DELL·E3 等所有最新功能同步可用国内网站

低调使用。推荐一个 GPT4 Turbo、Vision、GPTs、DELL·E3 等所有最新功能同步可用国内网站

在 11 月 6 日&#xff0c;万众期待的 OpenAI DevDay&#xff0c;ChatGPT 发布了一系列新的产品&#xff0c;其中推出了 GPT4 Turbo&#xff0c;并且将GPT4 Vision&#xff0c;DELLE3 等等能力全部集合到一起&#xff0c;不需要再分开使用&#xff0c;原来的局限的文本聊天也进…
阅读更多...
『 MySQL数据库 』插入查询结果

『 MySQL数据库 』插入查询结果

文章目录 &#x1f39f;️ 前言&#x1f39f;️ 创建一张结构相同的表&#x1f39f;️ 表内插入查询结果&#x1f3ab; 对表内数据进行去重&#x1f3ab; 配合ORDER BY排序后以及LIMIT分页对数据进行插入 &#x1f39f;️ 前言 在MySQL数据库中不仅可以直接根据字段类型等对数据…
阅读更多...
找不到 sun.misc.BASE64Decoder ，sun.misc.BASE64Encoder 类

找不到 sun.misc.BASE64Decoder ，sun.misc.BASE64Encoder 类

找不到 sun.misc.BASE64Decoder &#xff0c;sun.misc.BASE64Encoder 类 1. 现象 idea 引用报错 找不到对应的包 import sun.misc.BASE64Decoder; import sun.misc.BASE64Encoder;2. 原因 因为sun.misc.BASE64Decoder和sun.misc.BASE64Encoder是Java的内部API&#xff0c;通…
阅读更多...
Ubuntu安装nfs服务步骤

Ubuntu安装nfs服务步骤

Ubuntu安装nfs服务步骤 一、NFS&#xff1f; NFS&#xff1a;网络文件系统&#xff08;Network File system File&#xff09;缩写&#xff0c;可通过网络让不同的机器&#xff0c;不同操作系统之间可以彼此共享文件和目录。 二、安装 1.安装nfs服务器命令&#xff1a;sudo…
阅读更多...
【java】图书管理系统

【java】图书管理系统

完整代码链接&#xff1a;https://gitee.com/zeng-xuehui/Java_repository/tree/master/test_11_27_1/src我们在写这个系统时&#xff0c;首先需要搭建框架&#xff0c;再实现业务逻辑&#xff1b;图书管理系统是用户通过各种功能对图书进行操作的一个系统&#xff1b;我们需要…
阅读更多...
【LeetCode刷题】--90.子集II

【LeetCode刷题】--90.子集II

90.子集II class Solution {public List<List<Integer>> subsetsWithDup(int[] nums) {List<List<Integer>> ans new ArrayList<>();List<Integer> list new ArrayList<>();//排序后便于去重Arrays.sort(nums);dfs(0,nums,ans,lis…
阅读更多...
第二十章多线程总结

第二十章多线程总结

20.1 线程简介 世间有很多工作都是可以同时完成的。例如&#xff0c;人体可以同时进行呼吸、血液循环、思考问题等活用户既可以使用计算机听歌&#xff0c;也可以使用它打印文件。同样&#xff0c;计算机完全可以将多种活动同时进这种思想放在 Java 中被称为并发&#xff0c;而…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023