基于傅里叶变换的运动模糊图像恢复算法matlab仿真-编程知识

基于傅里叶变换的运动模糊图像恢复算法matlab仿真

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

4.1、傅里叶变换与图像恢复

4.2、基于傅里叶变换的运动模糊图像恢复算法原理

5.算法完整程序工程

1.算法运行效果图预览

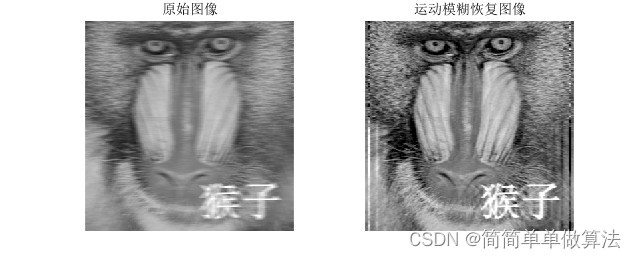
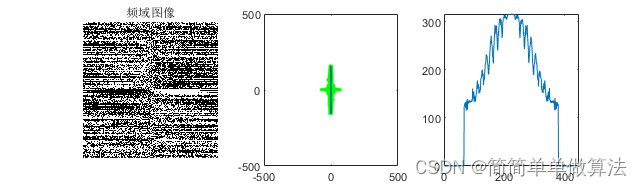
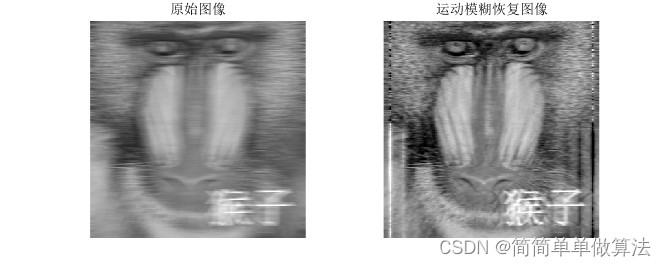
2.算法运行软件版本

matlab2022a

3.部分核心程序

%获取角度
img_fft2 = img_fft2/max(max(img_fft2));% 归一化处理  
[Rr,Cc]  = size(img_fft2);% 获取频谱尺寸  
img_x    = zeros(1,Rr*Cc); % 初始化x坐标数组  
img_y    = zeros(1,Rr*Cc);% 初始化y坐标数组  
idx      = 0;
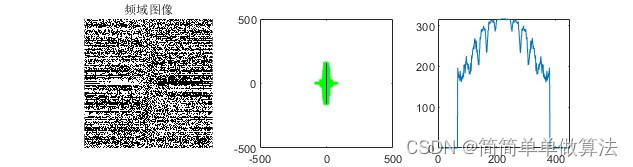
for i1 = 1:Rr% 遍历频谱的每一个像素  for j1 = 1:Ccif img_fft2(i1,j1) > 0.0005% 如果像素值大于阈值  idx        = idx+1;    % 计数器加1  img_x(idx) = i1+1-Rr/2;% 计算x坐标  img_y(idx) = j1+1-Cc/2;% 计算y坐标endend
end% 对x和y进行线性拟合，获取拟合参数p和统计信息s 
[p,s] = polyfit(img_x,img_y,1);
% 如果拟合的残差平方和大于4500  
if s.normr>4500% 交换x和y再次进行拟合  [p,s] = polyfit(img_y,img_x,1);% 计算角度（弧度转角度）  Angles= atan(p(1))/pi*180;% 调整角度值 Angles= 90-Angles;% 如果角度小于0度  % 加上180度if Angles<0Angles = Angles+180;end% 使用拟合参数计算y的拟合值  y_fit = polyval(p,img_x);subplot(132)plot(-img_y,img_x,'g.',img_x,-y_fit,'b');
elseAngles = atan(p(1))/pi*180;% 计算角度（弧度转角度） if Angles < 0% 如果角度小于0度 Angles = Angles +180;% 加上180度endy_fit = polyval(p,img_x);%求拟合后的y值;subplot(132)plot(-img_y,img_x,'g.',-y_fit,img_x,'b');
end
87

4.算法理论概述

运动模糊是由于摄像设备和目标之间的相对运动导致的一种图像降质现象。这种模糊会对图像的视觉质量和识别性能产生严重影响。为了解决这个问题，研究者们提出了各种图像恢复算法。其中，基于傅里叶变换的方法因其计算效率和恢复效果受到广泛关注。

4.1、傅里叶变换与图像恢复

傅里叶变换是一种将信号从时域转换到频域的数学工具。在图像处理中，傅里叶变换可以帮助我们分析图像的频率成分，进而实现去噪、压缩等操作。对于运动模糊图像恢复，傅里叶变换的主要作用是在频域中对模糊进行建模和分析。

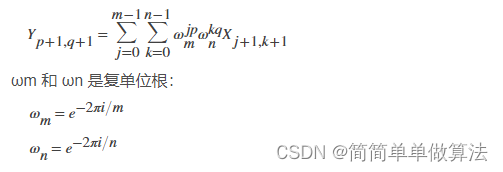
i 是虚数单位，p 和 j 是值范围从 0 到 m–1 的索引，q 和 k 是值范围从 0 到 n–1 的索引。在此公式中，X 和 Y 的索引平移 1 位，以反映 MATLAB® 中的矩阵索引。计算 X 的二维傅里叶变换等同于首先计算 X 每列的一维变换，然后获取每行结果的一维变换。换言之，命令 fft2(X) 等同于 Y = fft(fft(X).').'。