【面试HOT200】回溯篇

系列综述：
💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于【CodeTopHot300】进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证，所有代码均优先参考最佳性能。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

文章目录

    • 基础知识
    • 回溯基础算法模板
      • 组合问题
        • 无重复元素的组合
        • 有重复元素的组合
      • 排列问题
        • 无重复元素的全排列
        • 有重复元素的全排列
    • HOT200回溯相关题目
        • 39. 组合总和
        • 40. 组合总和 II
        • 93. 复原 IP 地址
        • 131. 分割回文串
        • 1005. K 次取反后最大化的数组和
    • 参考博客

😊点此到文末惊喜↩︎

基础知识

  1. 回溯算法 = 穷举 + 剪枝
    • 穷举：从一个选择开始，一步步尝试每一个可能的选择，如果某次选择导致问题无法解决，则回溯并选择另一种可能，直到找到一个可行的解或者穷举所有可能的解。
    • 剪枝：在搜索过程中，根据问题的限制条件，减少搜索空间，提高算法效率
  2. 作用
    • 在多个选择中搜索出满足条件的所有可能解
    • 一般地，组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。
  3. 回溯算法解决的问题一般为npc问题，难以使用常规算法进行解决
    • 组合问题：N个数里面按一定规则找出k个数的集合
      • 切割问题：一个字符串按一定规则有几种切割方式
      • 子集问题：一个N个数的集合里有多少符合条件的子集
    • 排列问题：N个数按一定规则选出M个，有几种排列方式
    • 棋盘问题：N皇后，解数独等等
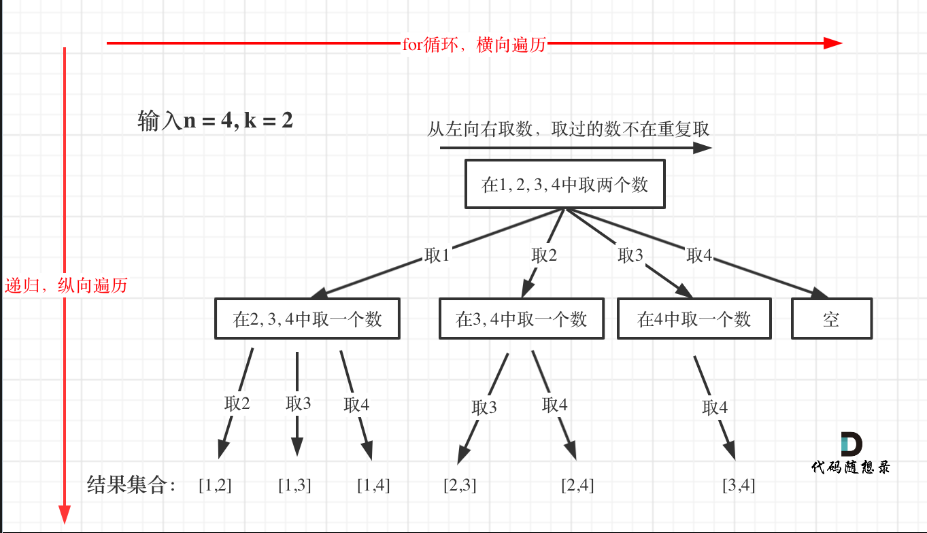
  4. 所有的回溯法解决的问题都可以抽象为树形结构
    • 根节点是总数据集合，树枝节点是可选数据集合
    • 叶子节点为根节点到叶子节点的路径的选择集合
      在这里插入图片描述
// 结果集和路径集
vector<vector<type> res;
vector<type> path;
void backtracking(vecotr<type> candidates, int startIndex) {// 针对当前选择的合法性判断auto is_ok = [](const type &data)->bool{// type中数据项的合法性判断};// 递归出口：结点剪枝，生成慢if (is_ok(val)) {res.push_back(path);return;}// 延申和回撤路径时，可能涉及多个状态标记变量的改动for (int i = startIndex; i < candidates.size(); ++i) {分叉剪枝判断（性能高）;// 状态延申改动path.push_back(candidates[i]);// 向下延申backtracking(剩余可选列表); // 回溯// 状态回撤改动path.pop_back();// 回撤延申}
}
// 主函数
vector<vector<int>> combine(vector<type>& candidates) {res.clear(); // 可以不写path.clear();// 可以不写backtracking(candidates, 0);return result;}

回溯基础算法模板

模板使用的初衷：将问题的输入转换成对应模板的输入格式，然后调用模板的函数（已经背诵的）进行快速的求解

组合问题

  1. 组合问题的复杂度
    • 时间复杂度： O ( C n k × k ) O(C_n^k × k) O(Cnk​×k)，总共有 C n k C_n^k Cnk​种组合，每种组合需要 O ( k ) O(k) O(k) 的时间复杂度
    • 空间复杂度： O ( n ) O(n) O(n)，递归深度为n，所以系统栈所用空间为 O ( n ) O(n) O(n)
无重复元素的组合
  1. 基本概述
    • 问题：从无重复元素的集合中选出K个元素组成组合，每个元素只能被选取一次，且选出的元素之间没有顺序之分。
    • 举例：从元素集合{1，2，3}中选择2个元素的组合为{(1,2)，(1,3)，(2,3)}。
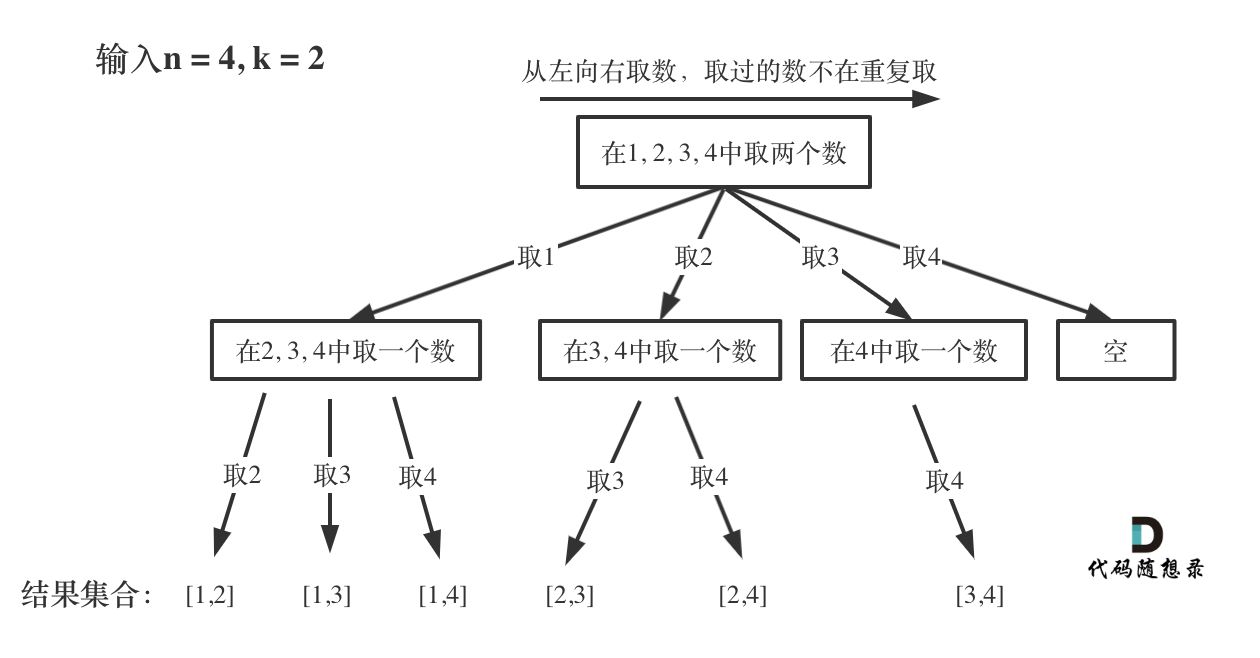
      在这里插入图片描述
  2. 代码
    • 解决的问题：给定一个线性表，求该线性表中满足条件的组合
    • 示例：求线性表中所有个数为target的结果。
    • 剪枝：列表中剩余元素(vec.size() - i) >= 所需需要的元素个数(target - path.size()) 
// 从候选集candidate中选出任意k个数组成的集合
vector<vector<int>> Backtracking(vector<int> &candidate, int k) {const int len = candidate.size();// 递归函数vector<int> path;			// 符合条件的路径vector<vector<int>> res;	// 符合条件的路径集合auto self = [&](auto &&self, int pos){// 递归出口：满足条件的路径加入结果集中if (path.size() == k) {res.push_back(path);return;}// i = start表示从之后剩余中选择for (int i = pos; i < len ; ++i) {if (i > len - (k-path.size())) continue;path.push_back(candidate[i]);	// 做出选择self(self, i+1);// key: 是i+1	// 递归path.pop_back();				// 撤销选择}};self(self, 0);return res;
}
有重复元素的组合
  1. 基本概述
    • 问题：从有重复元素的组合中选出若干元素组成组合，每个元素只能被选取一次，且选出的元素之间没有顺序之分。
    • 举例：从集合{1, 2, 2, 3}中选择2个元素的组合为{1, 2}、{1, 3}、{2, 2}、{2, 3}。
  2. 代码
    • 解决问题：给定一个线性表，求该线性表中满足条件的组合，因为有重复元素，所以选择重复元素时只能使用一次，否则会出现集合中的重复
vector<vector<int>> Backtracking(vector<int> &candidate, int k) {// 排序sort(candidate.begin(), candidate.end());// 递归匿名函数vector<int> path;vector<vector<int>> res;auto self = [&](auto &&self, int pos){if (path.size() == k) {res.push_back(path);return;}for (int i = pos; i < candidate.size(); ++i) {// key: i > pos。第一次选取到重复的数，不会影响后面if (i > pos && candidate[i] == candidate[i-1])continue;path.push_back(candidate[i]);self(self, i+1);path.pop_back();}};// 递归调用self(self, 0);return res;
}

排列问题

  1. 组合问题的复杂度
    • 时间复杂度： O ( n × n ! ) O(n×n!) O(n×n!)，一共 n ! n! n! 种组合，每种排列构造时间需要 O ( n ) O(n) O(n) 的时间复杂度
    • 空间复杂度： O ( n ) O(n) O(n)，递归深度为n，所以系统栈所用空间为 O ( n ) O(n) O(n)
无重复元素的全排列
  1. 基本概述
    • 问题：无重复元素的排列是指在给定一组不同的元素中，按照一定的顺序排列出所有可能的组合，每个元素只出现一次。
    • 举例：从集合{1, 2, 3}，则可以产生以下6种无重复元素的排列：{1, 2, 3}、{1, 3, 2}、{2, 1, 3}、{2, 3, 1}、{3, 1, 2}、{3, 2, 1}。
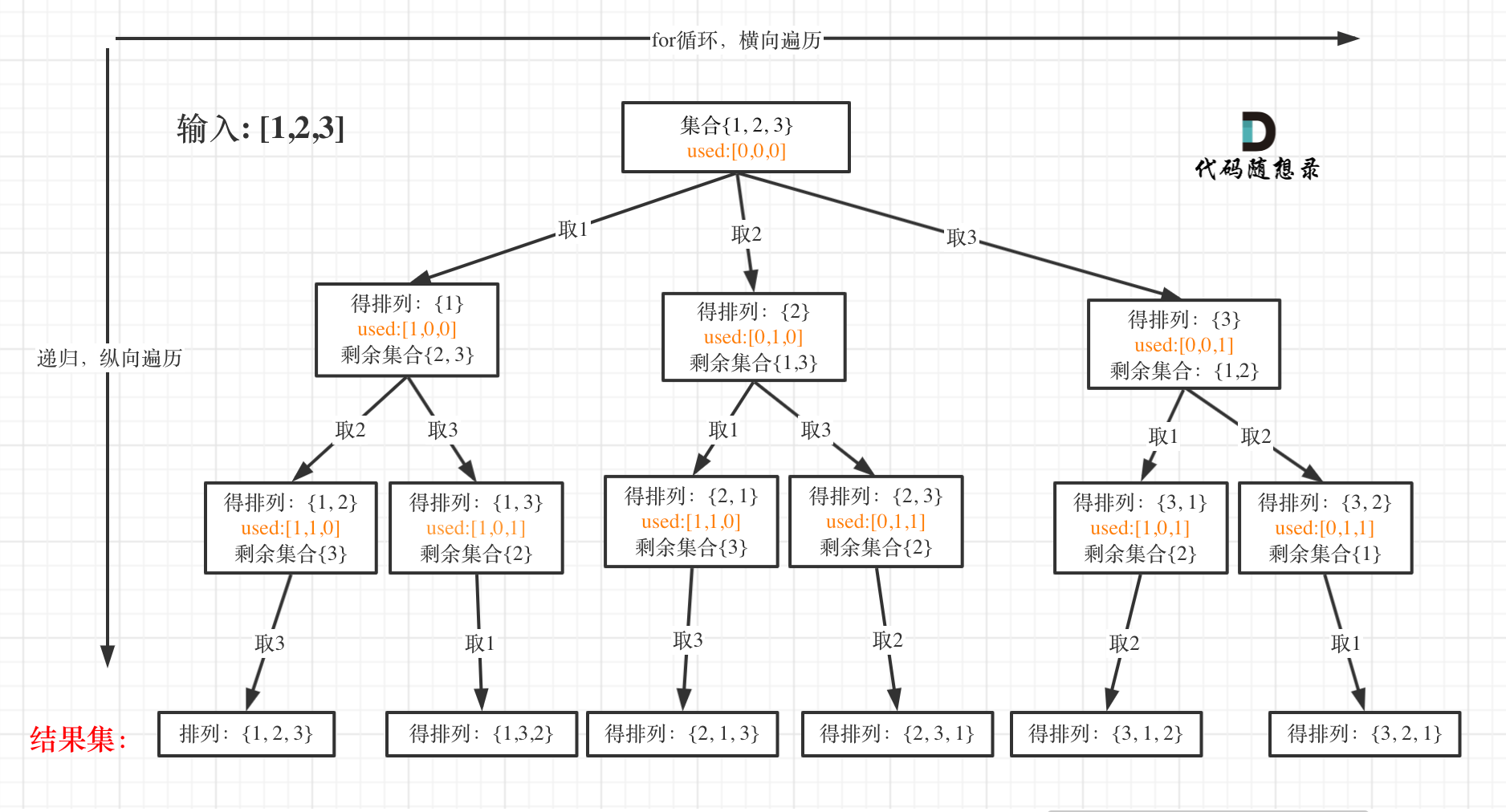
      在这里插入图片描述
  2. 代码
    • 不需要使用pos，每一个i对应一位
    vector<vector<int>> permute(vector<int>& candidate) {const int len = candidate.size();vector<int> path;				// 回溯路径vector<vector<int>> res;		// 回溯结果集vector<bool> used(len, false);	// 使用标记auto self = [&](auto &&self){	// 回溯算法if (path.size() == len) {res.push_back(path);return ;}for (int i = 0; i < len; ++i) {// path里已经收录的元素，直接跳过if (used[i] == true) continue;// 增加选择used[i] = true;path.push_back(candidate[i]);// 进行回溯self(self);// 撤回选择used[i] = false;path.pop_back();}};// 调用self(self);return res;
}
有重复元素的全排列

  1. 基本概述

    • 问题：无重复元素的排列是指在给定一组不同的元素中，按照一定的顺序排列出所有的不重复组合
    • 举例：从集合[1,1,2]，则可以产生无重复的全排列： [1,1,2], [1,2,1], [2,1,1]

  2. 代码

    • 产生重复解的原因：例如[1,1,2], 无法区分[1(0), 1(1), 2] 和[1(1), 1(0), 2] 这两种情况的解
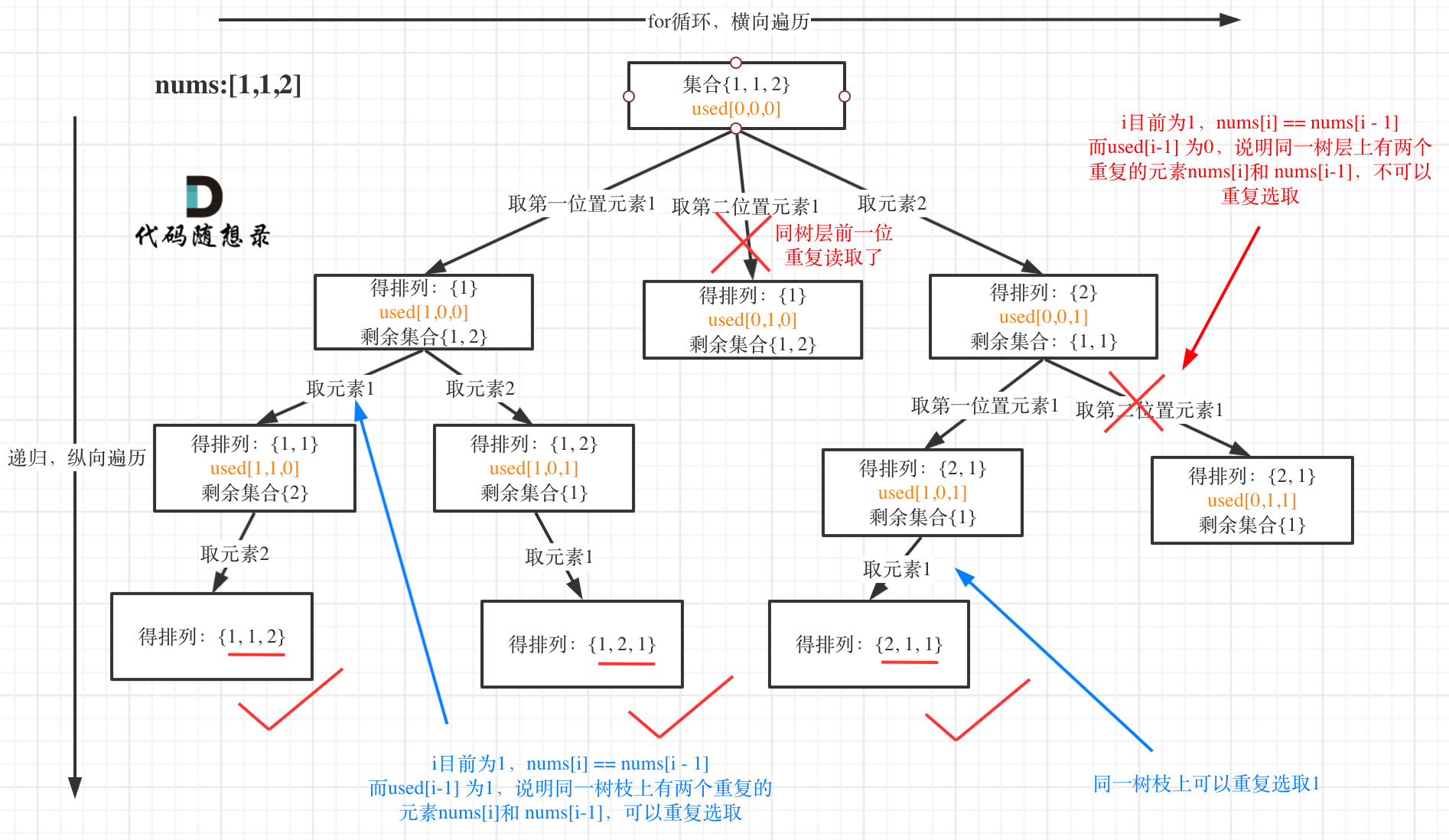
      在这里插入图片描述
    vector<vector<int>> permuteUnique(vector<int>& candidate) {const int len = candidate.size();sort(candidate.begin(), candidate.end());// 递归vector<int> path;vector<vector<int>> res;vector<bool> used(len, false);  // key：注意初始化auto self = [&](auto &&self){if (path.size() == len) {res.emplace_back(path);return ;}for (int i = 0; i < len; ++i) {// 有效的重复元素 && 前一个元素未被使用// 保证相同元素同层中只有第一个被使用if (i > 0 && candidate[i] == candidate[i-1] && used[i-1] == false) continue;if (used[i] == false) {used[i] = true;path.emplace_back(candidate[i]);self(self);used[i] = false;path.pop_back();}}};self(self);return res;
}// 哈希表处理重复解
vector<vector<int>> permuteUnique(vector<int>& candidate) {const int len = candidate.size();// 去重unordered_map<int, int> umap;for (auto &i : candidate) ++umap[i];// 回溯算法vector<vector<int> > res;vector<int> path;auto self = [&](auto &&self, int pos){// 递归出口if (pos == len) {res.push_back(path);return ;}for (auto &i : umap) {if (i.second == 0) continue;path.push_back(i.first);--i.second;self(self, pos+1);path.pop_back();++i.second;}};self(self, 0);return res;
}

HOT200回溯相关题目

39. 组合总和
  1. 题目
    • 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回
    • candidates 中的 同一个 数字可以 无限制重复被选取
    • 输入：candidates = [2,3,5], target = 4
    • 输出：[[2,2]]
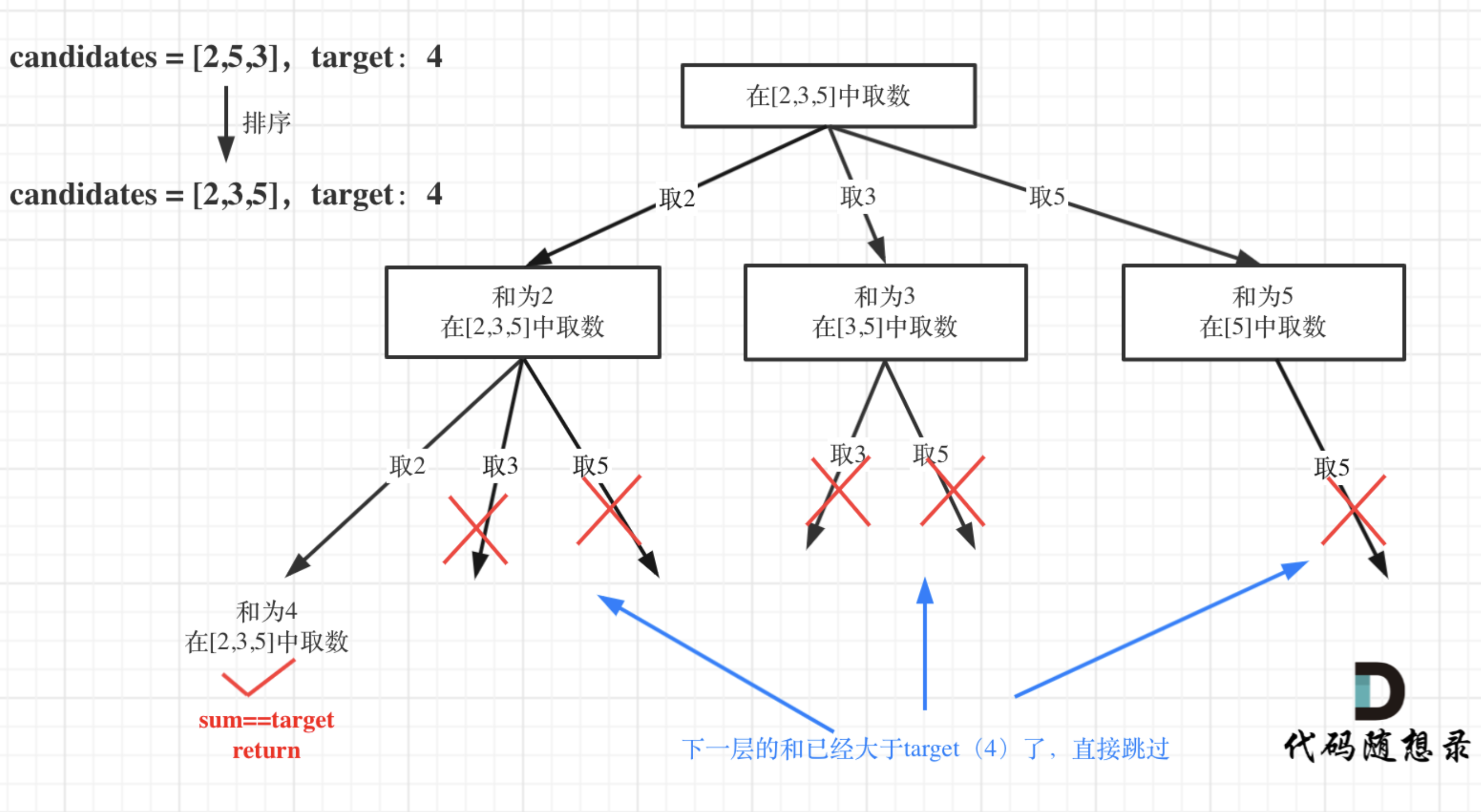
      在这里插入图片描述
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<vector<int>> res;vector<int> path;auto self =  [&](auto &&self, int pos, int sum){// 结束条件if (sum > target) return ;if (sum == target) {res.push_back(path);return ;}// 路径回溯for (int i = pos; i < candidates.size(); ++i) {sum += candidates[i];path.push_back(candidates[i]);self(self, i, sum);	// key: 不用i+1表示可重复读取当前值sum -= candidates[i];path.pop_back();}};self(self, 0, 0);return res;
}
40. 组合总和 II
  1. 题目
    • 给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。
    • 输入: candidates = [2,5,2,1,2], target = 5,
    • 输出：[ [1,2,2], [5] ]
  2. 代码
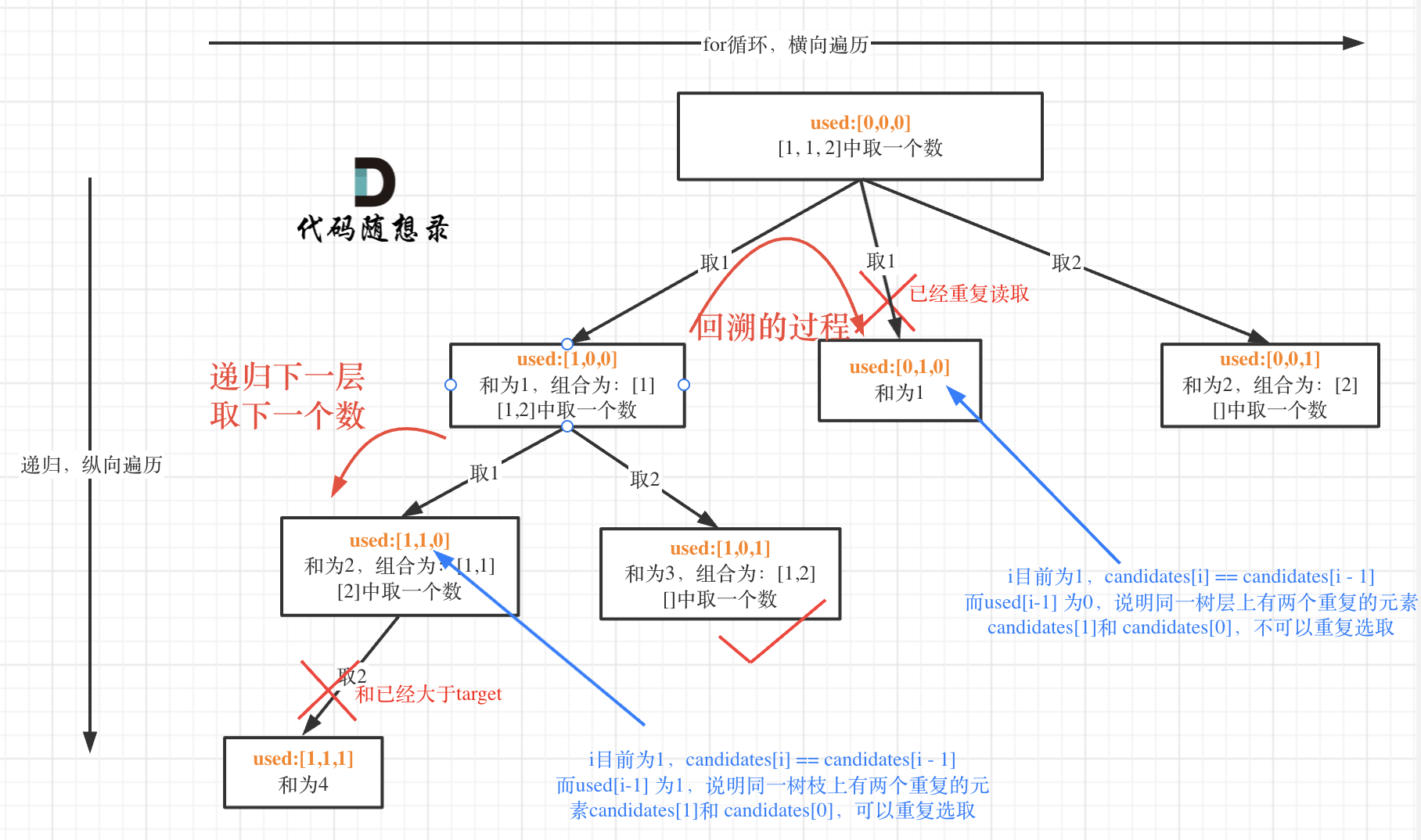
    在这里插入图片描述
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {const int len = candidates.size();sort(candidates.begin(), candidates.end());// 回溯部分vector<int> path;vector<vector<int>> res;vector<bool> used(len, false);int sum = 0;auto self = [&](auto &&self, int pos){// 结点剪枝if (sum == target) {res.emplace_back(path);return ;}for (int i = pos; i < len; ++i) {// 分叉剪枝: 性能高一些if (sum + candidates[i] > target) continue;if (i > 0 && candidates[i] == candidates[i-1] && used[i-1] == false) continue;if (used[i] == true) continue;used[i] = true;path.emplace_back(candidates[i]);sum += candidates[i];self(self, i+1);    // i+1表示每个元素不重复使用sum -= candidates[i];path.pop_back();used[i] = false;}};self(self, 0);return res;
}
93. 复原 IP 地址
  1. 题目
    • 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 ‘.’ 来形成
    • 输入：s = “25525511135”
    • 输出：[“255.255.11.135”,“255.255.111.35”]

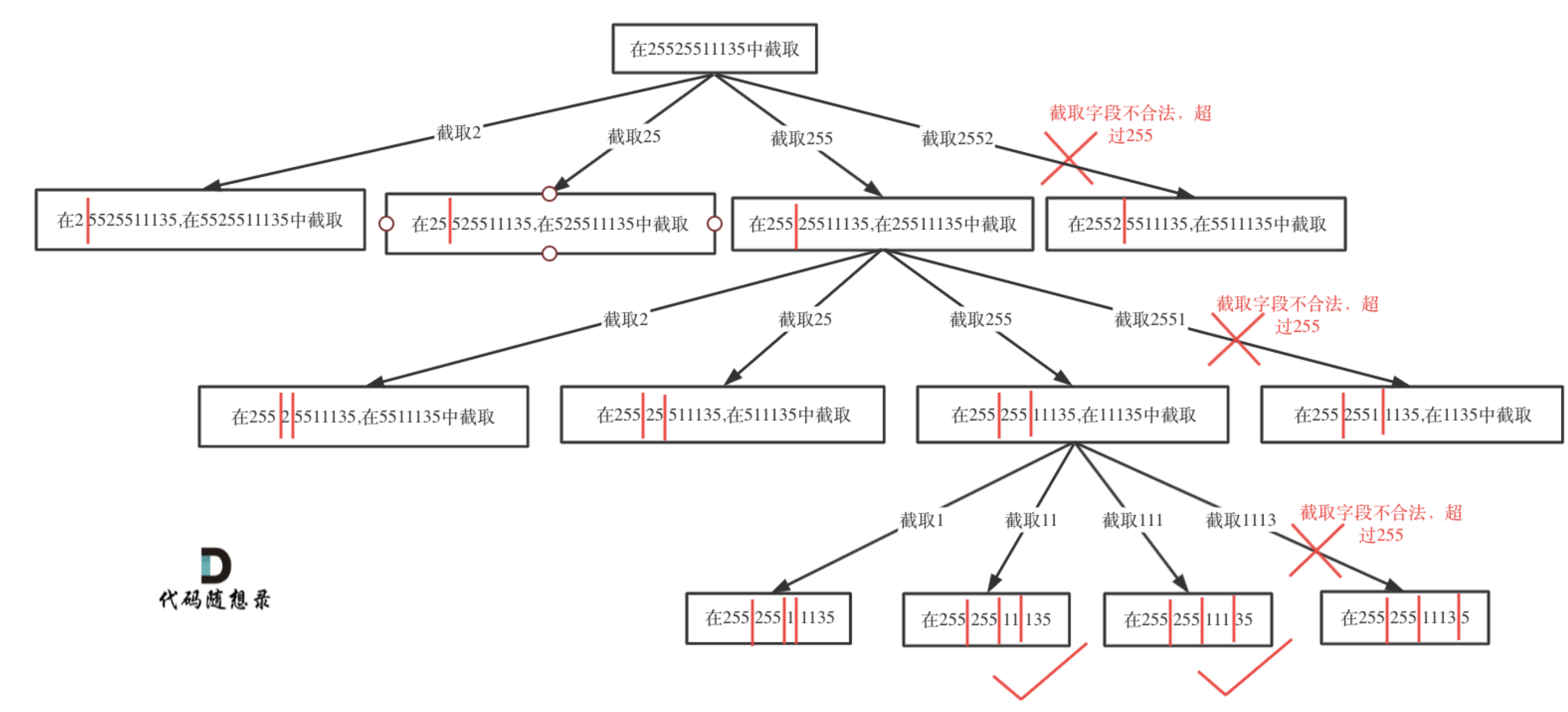
在这里插入图片描述

vector<string> restoreIpAddresses(string s) {const int len = s.size();// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法auto is_valid = [](const string& s, int start, int end) {cout << start <<' ' <<  end << endl;if (start > end) {return false;}if (s[start] == '0' && start != end) // 0开头的数字不合法return false;int num = 0;for (int i = start; i <= end; i++) {if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法return false;}num = num * 10 + (s[i] - '0');if (num > 255) { // 如果大于255了不合法return false;}}return true;
};
131. 分割回文串
  1. 131. 分割回文串
    • 获取[startIndex,i]在s中的子串s.substr(startIndex, i - startIndex + 1)
    // 判断是否为回文字符串
bool isPalindrome(const string& s, int start, int end) {for (int i = start, j = end; i < j; i++, j--) {if (s[i] != s[j]) {return false;}}return true;
}
// 基本的回溯
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
void backtracking (const string& s, int startIndex) {// 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了if (startIndex >= s.size()) {result.push_back(path);return;}for (int i = startIndex; i < s.size(); i++) {// 剪枝与枝的延长if (isPalindrome(s, startIndex, i)) {   // 是回文子串// 获取[startIndex,i]在s中的子串string str = s.substr(startIndex, i - startIndex + 1);path.push_back(str);} else {  // 不是回文，跳过continue;}backtracking(s, i + 1); // 寻找i+1为起始位置的子串path.pop_back(); // 回溯过程，弹出本次已经填在的子串}
}vector<vector<string>> partition(string s) {result.clear();path.clear();backtracking(s, 0);return result;
}
1005. K 次取反后最大化的数组和
  1. 1005. K 次取反后最大化的数组和
    • sort的使用：第三个参数为自定义的排序队则，在头文件#include
    • accumulate的使用：第三个参数为累加的初值，在头文件include
    static bool cmp(int a, int b) {return abs(a) > abs(b);// 绝对值的从大到小进行排序
}
int largestSumAfterKNegations(vector<int>& A, int K) {// 将容器内的元素按照绝对值从大到小进行排序sort(A.begin(), A.end(), cmp); // 在K>0的情况下，将负值按照绝对值从大到小依次取反for (int i = 0; i < A.size(); i++) { if (A[i] < 0 && K > 0) {A[i] *= -1;K--;}}// 如果K为奇数，将最小的正数取反if (K % 2 == 1) A[A.size() - 1] *= -1; // 求和return accumulate(A.begin(),A.end(),0);// 第三个参数为累加的初值，在头文件include<numeric>
}
少年，我观你骨骼清奇，颖悟绝伦，必成人中龙凤。
不如点赞·收藏·关注一波

🚩点此跳转到首行↩︎

参考博客

  1. 「代码随想录」47. 全排列 II:【彻底理解排列中的去重问题】详解
  2. codetop

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/236223.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Golang语言基础之切片

Golang语言基础之切片

概述 数组的长度是固定的并且数组长度属于类型的一部分&#xff0c;所以数组有很多的局限性 func arraySum(x [3]int) int{sum : 0for _, v : range x{sum sum v}return sum } 这个求和函数只能接受 [3]int 类型&#xff0c;其他的都不支持。 切片 切片&#xff08;Slic…
阅读更多...
leetCode 131.分割回文串 + 动态规划 + 回溯算法 + 优化 + 图解 + 笔记

leetCode 131.分割回文串 + 动态规划 + 回溯算法 + 优化 + 图解 + 笔记

我的往期文章&#xff1a; leetCode 647.回文子串 动态规划 优化空间 / 中心扩展法 双指针-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133883091?spm1001.2014.3001.5501leetCode 131.分割回文串 回溯算法 图解 笔记-CSDN博客https://blog.csdn.n…
阅读更多...
i己学助力构建幼教智能时代家园共育新模式

i己学助力构建幼教智能时代家园共育新模式

近日,为探索智能时代幼儿教育的智慧化解决方案,智能时代赢之道——2023幼教智能时代精英论坛在北京成功举办。在会议现场,来自全国各地的幼儿教育专家、园长、教师汇聚一堂,针对智能时代幼儿园所应该如何变革展开分享和讨论,“i己学智慧课堂”同期发布。 “在1-6年级阶段,平均…
阅读更多...
HTML5+CSS3小实例：纯CSS实现文字组成肖像特效

HTML5+CSS3小实例：纯CSS实现文字组成肖像特效

实例：纯CSS实现文字组成肖像特效 技术栈：HTML+CSS 效果： 源码： 【HTML】 <!DOCTYPE html> <html><head><meta http-equiv="content-type" content="text/html; charset=utf-8"><meta name="viewport" conten…
阅读更多...
linux服务器环境搭建（使用yum 安装mysql、jdk、redis）

linux服务器环境搭建（使用yum 安装mysql、jdk、redis）

一：yum的安装 1：下载yum安装包并解压 wget http://yum.baseurl.org/download/3.2/yum-3.2.28.tar.gz tar xvf yum-3.2.28.tar.gz 2.进入yum-3.2.28文件夹中进行安装，执行安装指令 cd yum-3.2.28 sudo apt install yum 3.更新版本 yum check-update yum update yum cle…
阅读更多...
Spring三级缓存处理循环依赖的过程

Spring三级缓存处理循环依赖的过程

Spring三级缓存 Spring三级缓存是什么&#xff1f; 一级缓存&#xff1a;单例池。存放的是完整的Bean对象。经过完整的生命周期。二级缓存&#xff1a;存放需要提前暴露的Bean对象。也就不完整的Bean对象。需要提前暴露就是指&#xff0c;可能会被循环依赖。(这里可能需要用代…
阅读更多...
Reactor网络线程模型

Reactor网络线程模型

目录 传统下网络服务模型 事件监听模型 NIO核心概念 单线程Reactor模式 多线程Reactor模式 Kafka 的网络设计 主要概念 类比思维理解 参考文章 传统下网络服务模型 线程太多无法处理大规模请求 事件监听模型 NIO核心概念 nio是实现reactor模式的底层API代码 单…
阅读更多...
vue3+element-plus+vue-cropper实现裁剪图片上传

vue3+element-plus+vue-cropper实现裁剪图片上传

1.vue3element-plusvue-cropper实现裁剪图片 element-UI官网element-plus官网vue-croppervue3使用vue-cropper安装&#xff1a;npm install vue-croppernext 2.vue-cropper插件&#xff1a; <vue-cropper :img"option.img" /><script setup>import {reac…
阅读更多...
Pycharm中使用matplotlib绘制动态图形

Pycharm中使用matplotlib绘制动态图形

Pycharm中使用matplotlib绘制动态图形 最终效果 最近用pycharm学习D2L时发现官方在jupyter notebook交互式环境中能动态绘制图形&#xff0c;但是在pycharm脚本环境中只会在最终 plt.show() 后输出一张静态图像。于是有了下面这段自己折腾了一下午的代码&#xff0c;用来在pych…
阅读更多...
(项目已开源)社区求助 哪位大佬能不能帮我 将box1 audio 和 box2 slider滑块 和 box3 歌词滚动区域 进行联动

(项目已开源)社区求助 哪位大佬能不能帮我 将box1 audio 和 box2 slider滑块 和 box3 歌词滚动区域 进行联动

(项目已开源)社区求助 哪位大佬能不能帮我 将box1 audio 和 box2 slider滑块 和 box3 歌词滚动区域 进行联动 链接&#xff1a;https://pan.baidu.com/s/16lpEW6L5jrHfhsG7EXocLw?pwdkryy 提取码&#xff1a;kryy <!--社区求助 哪位大佬能不能帮我 将box1 audio 和 box2 s…
阅读更多...
Vue的Nuxt项目部署在服务器，pm2动态部署和npm run build静态部署

Vue的Nuxt项目部署在服务器，pm2动态部署和npm run build静态部署

Nuxt项目的部署有两种方式&#xff0c;一种是静态部署&#xff0c;一种是动态部署 静态部署需要关闭项目的ssr功能&#xff0c;动态部署则不需关闭&#xff0c;所以怎么部署项目就看你用不用ssr功能了 。 1.静态部署 先说静态部署&#xff0c;很简单&#xff0c;只需要在nuxt…
阅读更多...
蓝桥杯每日一题2023.11.30

蓝桥杯每日一题2023.11.30

题目描述 九数组分数 - 蓝桥云课 (lanqiao.cn) 题目分析 此题目实际上是使用dfs进行数字确定&#xff0c;每次循环中将当前数字与剩下的数字进行交换 eg.1与2、3、4、、、进行交换 2与3、4、、、进行交换 填空位置将其恢复原来位置即可&#xff0c;也就直接将其交换回去即可…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023