0.前提
上一期,我们简单的介绍了一些有关机器学习的内容。学习机器学习的最终目的是为了服务我未来的毕设选择之一——智能小车,所以其实大家完全可以根据自己的需求来学习这门课,我做完另一辆小车后打算花点时间去进行一次徒步行,回来就开始专心积累底层知识了(回归轻松时刻,去考试,本来预期是一个学期更新大概25篇文章的,现在看其实已经完全超过预期了)。
1.线性回归
1.线性回归的概念
线性回归:一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。
如图为单变量的线性回归,蓝点为真实数据,红点为预测数据,红点与红线重合度越高,数据拟合的效果越好。
2.符号定义
·代表训练集中样本的数量
·代表特征的数量
·代表特征/输入变量
·代表目标变量/输出变量
·代表训练集中的样本
·代表第
个观察样本
·代表学习算法的解决方案或函数也称为假设
·代表预测值
·是特征矩阵中的第
行,是向量
·是代表特征矩阵中第
行的第
个特征
3.算法流程
·损失函数:度量样本预测的错误程度,损失函数值越小,模型就越好。常用的损失函数包括:0-1损失函数、平方损失函数、绝对损失函数、对数损失函数等;损失函数采用平方和损失:
,损失函数的1/2是为了便于计算,使对平方项求导后的常数系数为1。
·代价函数:也称成本函数,度量全部样本集的平均误差。常用的代价函数包括均方误差、均方根误差、平均绝对误差等;残差平方和:
。
·目标函数:代价函数和正则化函数,最终要优化的函数。
4.线性回归求解
求解 :的一组
,常见的求残差平方和最小的方法为最小二乘法和梯度下降法。
2.最小二乘法(LSM)
·其实就是求最小
3.梯度下降
梯度下降有3种形式:批量梯度下降、随机梯度下降、小批量梯度下降。
1.批量梯度下降(BGD)
批量梯度下降:梯度下降的每一步中,都用到了所有的训练样本。
参数更新: (同步更新
,
),
代表学习率,
代表梯度。
2.随机梯度下降(SGD)
随机梯度下降:梯度下降的每一步中,用到一个样本,在每一次计算后更新参数,而不需要将所有的训练集求和。
参数更新:(同步更新
,
)
3.小批量梯度下降(MBGD)
4.梯度下降与最下二乘法的比较
1.梯度下降
需要选择学习率,要多次迭代,当特征数量
较大时能较好适用,适用各种类型的模型。
2.最小二乘法
不需要选择学习率,一次计算得出,需要计算
,如果特征数量
较大则运算代价大,因为矩阵逆得计算时间复杂度为0(
),一般当
小于10000时可以接受,只适用于线性模型,不适合逻辑回归等其他模型。
5.数据归一化/标准化
1.作用
标准化/归一化可以提升模型精度和加速模型收敛。
2.归一化(最大-最小规范化)
,将数据映射到[0,1]区间,数据归一化的目的是使得各特征对目标变量得影响一致,会将特征数据进行伸缩变化,所以数据归一化是会改变特征数据分布的。
3.Z-Score标准化
,其中
,
,处理后的数据均值为0,方差为1,数据标准化为了不同特征间具备可比性,经过标准化变换后的特征数据分布没有改变,当数据特征取值范围或单位差异较大时,最好做标准化处理。
4.是否需要做数据归一化/标准化
1.需要
线性模型,如基于距离度量的模型包括KNN(K近邻)、K-means聚类、感知机和SVM。另外,线性回归类的几个模型一般情况下也是需要做数据归一化/标准化处理的。
2.不需要
6.正则化
1.拟合

注释:拟合就好比成绩与刷题量之间的关系:欠拟合就是你刷题量特别少,考试得到的分数比你想象中的要低,这就说明欠拟合了;过拟合就是你知道刷题能提高成绩,然后一天16个小时都在刷题,是的你成绩变高了,但是你只是读了万卷书没能行万里路,这就是过拟合了;正合适就是,你刷了一定量的题,成绩不错,同时你也行了万里路,这就是正合适。
2.处理过拟合
1.获取更多的训练数据
使用更多的数据能有效解决过拟合,更多的数据样本能让模型学习更多更有效的特征,减少噪声影响。
2.降维
丢弃一些偏差较大的样本特征,手动选择保留的特征,也可以使用一些模型选择算法。
3.正则化
保留所有特征,减少参数大小,可以改善或减少过拟合问题。
4.集成学习
将多个模型集成在一起,来降低单一模型的过拟合风险。
3.处理欠拟合
1.添加新特征
特征不足或者现有特征与样本标签相关性不强时,模型容易欠拟合。挖掘组合新特征,效果会有所改善。
2.增加模型复杂度
简单模型学习能力差,增加模型的复杂度可以使模型有更强的拟合能力。例如:线性模型中添加高次项,神经网咯模型中增加网络层数或神经元个数等。
3.减小正则化系数
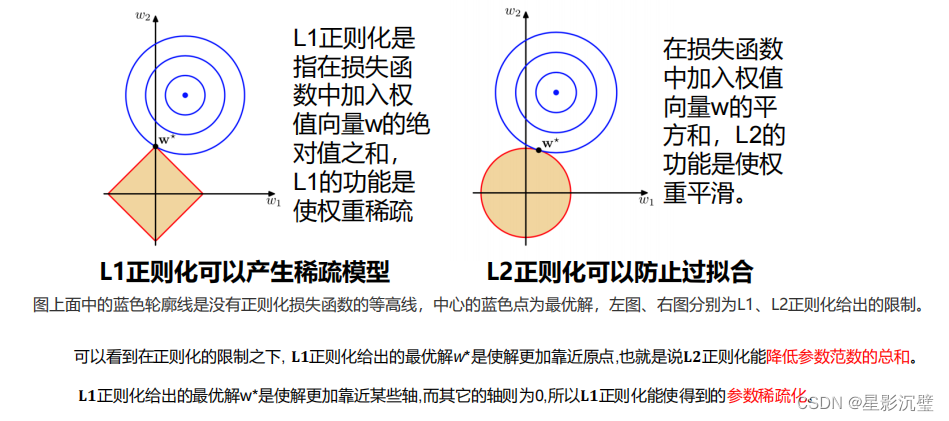
4.正则化
·λ为正则化系数,调整正则化项与训练误差的比例,λ>0。
·1≥ρ≥0为比例系数,调整L1正则化与L2正则化的比例。
1.L1正则化
,(Lasso回归)
2.L2正则化
,(岭回归)
3.Elastic Net
,(弹性网络)
7.回归的评价指标
代表第
个样本的真实值;
代表第
个样本的预测值;
为样本个数。
1.均方误差(MSE)
2.平均绝对误差(MAE)
3.均方跟误差(RMSE)