「SPOJ2666」QTREE4 - Query on a tree IV-编程知识

「SPOJ2666」QTREE4 - Query on a tree IV

news/2025/1/23 17:43:44/文章来源:https://www.cnblogs.com/keysky/p/18688268

题目概述

对一棵树维护两种操作：翻转某个点的颜色，求 \(max\{ dist_{u, v} \}\) 且满足 \(u\) 的颜色和 \(v\) 的颜色都是白色（ \(u,v\) 可以相同）。

思路

首先考虑若没有修改，给定带颜色的 \(N\) 个点怎么查询。
经典办法是树形 \(\text{dp}\) ，定义\(mx_u\) 表示在 \(u\) 的子树中从 \(u\) 出发距离最远的白点的距离，\(se_u\) 表示在 \(u\) 的子树中从 \(u\) 出发且不进入 \(mx_u\) 表示白点的子树距离最远的白点的距离，最后答案就是

\[\max_{ u \in [1, n] }\{ mx_u + se_u \} \]

现在考虑动态维护这一个 \(\text{dp}\) ，由于修改结点 \(u\) 的颜色后更新 \(dp\) 状态是在从 \(u\) 到根结点的链上更新 \(\text{dp}\) 值，同时 \(\text{dp}\) 的更新可以写作线段树的合并区间类型，所以可以考虑使用树链剖分，这样对于从 \(u\) 更新到根结点最多只会经过 \(\log N\) 条重链，同时线段树上的单点修改，区间合并花费 \(O(\log N)\) ，可以在 \(O(N log^2 N)\) 的时间内完成此题。

做法

对于结点 \(u\) 记录 \(mx(u)\) 表示在 \(u\) 的子树中从 \(u\) 出发且不走中重子结点距离最远的白点的距离，\(se(u)\) 表示在 \(u\) 的子树中从 \(u\) 出发且不进入 \(mx(u)\) 表示白点的子树和 \(u\) 的重子结点距离最远的白点的距离，如果不存在，都记为 \(- \infty\) 。

概述

首先对树进行轻重链剖分。

因为每一条重链在 \(\text{dfs}\) 序上都是一段连续的区间，所以对于每一条重链开一棵线段树维护 \(\text{dfs}\) 序上的区间信息。

对于线段树上某一点维护区间 \([l, r]\) 定义

\(topdis\) :从 \(dfs\) 序为 \(l\) 的点，即当前区间所表示的链的顶端向其子树出发，不进入 \(dfs\) 序为 \(r\) 的重子结点的子树所能到达的最远的白点的距离
\(bottomdis\) :从 \(dfs\) 序为 \(r\) 的点，即当前区间所表示的链的底端出发，只在 \(dfs\) 序为 \(l\) 的子树中前进所能到达的最远的白点的距离
\(val\) :记 \(dis(u, v)\) 表示 \(u\) 到 \(v\) 的距离，原树中所有满足 \(dfn_{\text{LCA}(u, v)} \in [l, r]\) 的点对 \((u, v)\) 中最大的 \(dis(u, v)\)

因为要开多棵线段树，所以要动态开点，同时记录 \(rt_u\) 表示以 \(u\) 为 \(top\) 的重链的线段树的根结点编号。

现在假设我们已经维护好所有线段树（画大饼，展望未来），设 \(val_i\) 表示重链 \(i\) 的线段树的根结点的 \(val\)（\(i\) 为该重链的 \(top\)），那么答案就是 \(\max_{ i \in \{ u | \exists v, top_v = u \}} \{ val_i \}\) 。

树链剖分

维护

先来聊聊线段树中的区间合并，设当前区间为 \([l, r]\) ，结点为 \(id\)，定义 \(dis(u, v)\) 表示 \(u\) 到 \(v\) 的距离，左儿子为 \(ls\) ，右儿子为 \(rs\)，\(rnk_i\) 表示 \(dfs\) 序为 \(i\) 的结点编号，对于 \(topdis\) ，我们可以直接继承左儿子的 \(topdis\) ,也可以走过整段左儿子表示的链进入右儿子，并走右儿子的 \(topdis\) 。即

\[topdis_{id} \leftarrow max( topdis_{ls} , dis(rnk_l, rnk_{mid + 1}) + topdis_{rs}) \]

像这样
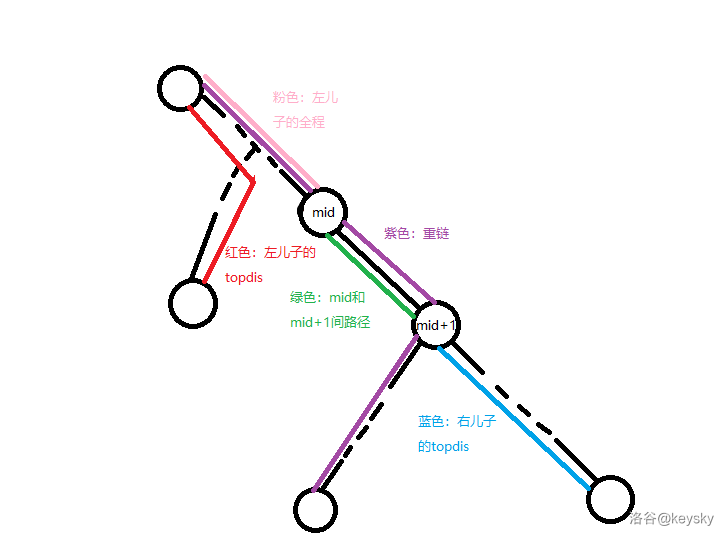
合并topdis
可走路径即图中的红色路径或粉色路径+绿色路径+蓝色路径，对应合并时取 \(max\) 的两个数。

\(bottomdis\)同理，即

\[bottomdis_{id} \leftarrow max( bottomdis_{rs} , dis(rnk_{mid}, rnk_r) + bottomdis_{ls}) \]

对于 \(val\) ，我们可以继承左右儿子的 \(val\) ，也可以从左儿子中的点走到右儿子中，即走左儿子的 \(bottomdis\) ，过 \((mid, mid + 1)\) ，走右儿子的 \(topdis\) ，转移即

\[val_{id} \leftarrow \max \{ val_{ls}, val_{rs}, bottomdis_{ls} + dis(rnk_{mid}, rnk_{mid + 1}) + topdis_{rs} \} \]

对于线段树中的叶子结点 \(u\)，可以利用 \(mx(u)\) 和 \(se(u)\) 更新。

因为 \(mx(u)\) 和 \(se(u)\) 的定义都不局限于当前重链，所以在更新当前重链前要把挂在该重链上的所有重链更新完，这一点乍一想很恶心，其实只需要对于 \(dfs\) 序反过来遍历并依次建树，因为对于挂在某条重链上的所有重链一定是在该重链遍历完再进行遍历（至少我的写法是这样）。

假设知道了 \(mx(u)\) 和 &se(u)& ，我们怎么更新 \(u\) 呢？我们分两种情况讨论：

结点 \(rnk_u\) 为白色，\(topdis_u, bottomdis_u \leftarrow max(mx(rnk_u), 0)\) ，因为可以以 \(rnk_u\) 为起点和终点，所以与 \(0\) 取 \(max\)（后面就不解释了），\(val_u \leftarrow \max \{ mx(rnk_u), mx(rnk_u) + se(rnk_u), 0 \}\)
结点 \(rnk_u\) 为黑色，\(topdis_u, bottomdis_u \leftarrow mx(rnk_u), val_u \leftarrow mx(rnk_u), mx(rnk_u) + se(rnk_u)\)

\(mx(rnk_u)\) 表示以 \(rnk_u\) 作为路径结尾的答案，\(mx(rnk_u) + se(rnk_u)\) 表示将以 \(rnk_u\) 为路径结尾的两条路径拼起来的答案。

现在考虑维护 \(mx(u)\) 和 \(se(u)\) ，由于我们会删除或加入白色点，所以用一个支持随机删除的堆来维护，这里我们可以偷懒使用\(\text{STL}\) 中的multiset，对每一个结点开一个堆，初始化时遍历 \(u\) 的轻儿子，用已更新好的重链来更新 \(u\) ，设 \(v\) 为 \(u\) 的轻儿子， \(id\) 为 \(v\) 所在重链的线段树的根结点，即插入 \(topdis_{id} + dis(u, v)\) 到 \(u\) 的堆中。

查询

对于每一条重链都会诞生一个答案，同时会实时修改，因为我们已经维护了一个支持随机删除和插入的堆，所以可以直接定义一个堆 \(ans\) 表示所有重链的答案的集合，查询时直接取出 \(ans\) 的堆顶元素即可。

修改

与树链剖分的板子相同，不过只有一个点 \(u\) ，所以单说跳的部分更简洁，但对于修改其实更加复杂。

首先，对于当前点 \(u\) ，它会影响到 \(fa_{top_u}\) 的 \(mx\) 和 \(se\) ，所以要在修改 \(u\) 前要消除对 \(fa_{top_u}\) 的影响，然后又要在修改后更新对于被撤销影响的位置的 \(mx\) 和 \(se\) ，即在 \(u\) 时删除 \(fa_{top_u}\) 的堆中的 \(topdis_{rt_{top_u}} + dis_{top_{u}} - dis_{fa_{top_{u}}}\) ，在 \(u\) 跳到 \(fa_{top_u}\) 后插入 \(topdis_{rt_{top_u}} + dis_{top_{u}} - dis_{fa_{top_{u}}}\) 。

然后，要修改 \(ans\) 这个堆，删除原本答案 \(val_{rt_{top_u}}\) ，修改后再插入新答案 \(val_{rt_{top_u}}\) 。

现在所有做法和细节就基本上讲完，最后还是要落到代码实现上，虽然说不算最长的那一类，但实现细节很多，建议理清思路后再打，不然盲目抄题解收获不大。

Code

/*
address:https://vjudge.net/problem/SPOJ-QTREE4
AC 2025/1/23 14:54
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int INF = 0x3f3f3f3f;
int n, q;
struct edge {int to, w;
};
vector<edge>G[N];
bool col[N];
struct Heap { // 支持随机删除堆multiset<int, greater<int>>s;inline void insert(int x) { s.insert(x); }inline void erase(int x) {auto it = s.lower_bound(x);if (it != s.end()) s.erase(it);}inline int mx() { return s.empty() ? -INF : *s.begin(); }inline int se() {if (s.size() <= 1) return -INF;auto it = s.begin();it++;return *it;}
}a[N], ans;
/*
a[i].mx：在i的子树中离i最远的白点的距离
a[i].se：在i的子树中离i次远且与mx只在i相交的白点的距离
ans：每条重链的答案集合
*/
int siz[N], dis[N], dfn[N], rnk[N], top[N], fa[N], son[N], len[N]; // len[i]：重链i的长度
int rt[N], L[N], R[N]; // 每个重链的线段树的根节点和管辖区间
inline void dfs1(int u) {siz[u] = 1;son[u] = 0;for (auto e : G[u])if (e.to != fa[u]) {fa[e.to] = u;dis[e.to] = dis[u] + e.w;dfs1(e.to);siz[u] += siz[e.to];if (siz[son[u]] < siz[e.to]) son[u] = e.to;}
}
int cntn;
inline void dfs2(int u) {dfn[u] = ++cntn;rnk[cntn] = u;len[top[u]]++;if (!son[u]) return;top[son[u]] = top[u];dfs2(son[u]);for (auto e : G[u])if (e.to != son[u] && e.to != fa[u]) {top[e.to] = e.to;dfs2(e.to);}
}
int nodecnt;
#define ls (seg[id].lc)
#define rs (seg[id].rc)
#define mid (l + r >> 1)
struct Segment {int lc, rc;int topdis, bottomdis, val;/*topdis:离该重链顶部最远的白点的距离bottomdis:离该重链底部最远的白点的距离val:该重链的答案*/
}seg[N << 2]; // 动态开点，对每条重链开一颗线段树
inline void merge(int id, int l, int r) {seg[id].topdis = max(seg[ls].topdis, dis[rnk[mid + 1]] - dis[rnk[l]] + seg[rs].topdis);// 左儿子的顶端，整段左儿子+右儿子顶端seg[id].bottomdis = max(seg[rs].bottomdis, dis[rnk[r]] - dis[rnk[mid]] + seg[ls].bottomdis);//同理seg[id].val = max({ seg[ls].val, seg[rs].val, seg[ls].bottomdis + dis[rnk[mid + 1]] - dis[rnk[mid]] + seg[rs].topdis });// 左儿子答案，右儿子答案，左儿子底端+中间的边+右儿子底端
}
inline void build(int id, int l, int r) {if (l == r) {int u = rnk[r];for (auto e : G[u])if (e.to != fa[u] && e.to != son[u]) a[u].insert(seg[rt[top[e.to]]].topdis + e.w); //从已更新完的重链转移，且两个区间不能相交，否则转移失效int mx = a[u].mx(), se = a[u].se();seg[id].topdis = seg[id].bottomdis = max(mx, 0); //初始所有点都是白点seg[id].val = max({ mx, mx + se, 0 });return;}ls = ++nodecnt;rs = ++nodecnt;build(ls, l, mid);build(rs, mid + 1, r);merge(id, l, r);
}
inline void change(int id, int l, int r, int x, int sontop) {if (l == r) {if (x != sontop) a[x].insert(seg[rt[sontop]].topdis + dis[sontop] - dis[x]); //更新被撤销的距离影响int mx = a[x].mx(), se = a[x].se();if (col[x]) { // 白点可以以自己为起点，与0取maxseg[id].topdis = seg[id].bottomdis = max(mx, 0);seg[id].val = max({ 0, mx, mx + se });}else {seg[id].topdis = seg[id].bottomdis = mx;seg[id].val = mx + se;}return;}if (dfn[x] <= mid) change(ls, l, mid, x, sontop);else change(rs, mid + 1, r, x, sontop);merge(id, l, r);
}
inline void modify(int u) {int sontop = u; // sontop：记录撤销对当前重链贡献的那条贡献while (u != 0) {ans.erase(seg[rt[top[u]]].val);if (fa[top[u]]) a[fa[top[u]]].erase(seg[rt[top[u]]].topdis + dis[top[u]] - dis[fa[top[u]]]); //撤销对父亲重链距离的影响change(rt[top[u]], L[top[u]], R[top[u]], u, sontop);ans.insert(seg[rt[top[u]]].val);sontop = top[u];u = fa[top[u]];}
}
inline void init() {dfs1(1);top[1] = 1;dfs2(1);for (int i = n;i >= 1;i--)if (rnk[i] == top[rnk[i]]) {rt[rnk[i]] = ++nodecnt;L[rnk[i]] = i, R[rnk[i]] = i + len[rnk[i]] - 1;build(rt[rnk[i]], i, i + len[rnk[i]] - 1);ans.insert(seg[rt[rnk[i]]].val);}
}
int main() {scanf("%d", &n);for (int i = 1;i < n;i++) {int u, v, w;scanf("%d%d%d", &u, &v, &w);G[u].push_back({ v, w });G[v].push_back({ u, w });}init();for (int i = 1;i <= n;i++) col[i] = true;scanf("%d", &q);int white = n;while (q--) {char op[2];scanf("%s", op);if (op[0] == 'C') {int u;scanf("%d", &u);col[u] ^= 1;white += col[u] ? 1 : -1;modify(u);}elseif (white == 0) puts("They have disappeared.");else printf("%d\n", ans.mx());}return 0;
}