算法题：求所需的最小的书包数量（拓展拓展再拓展~）-编程知识

算法题：求所需的最小的书包数量

现在有一种书包，这种书包只有两个书槽（即最多只能放下两本书。），并且一个这种书包只能装下N千克的书。现在有一个数组，数组元素是每本书的重量（千克）。问：完全装下这堆书，需要多少个书包？

题解如下：

正向暴力法

解析：

首先，很容易能想到的一个解法就是暴力解法。

贪心思想：我们先让两本最重的书先结合！
1. 先倒序。
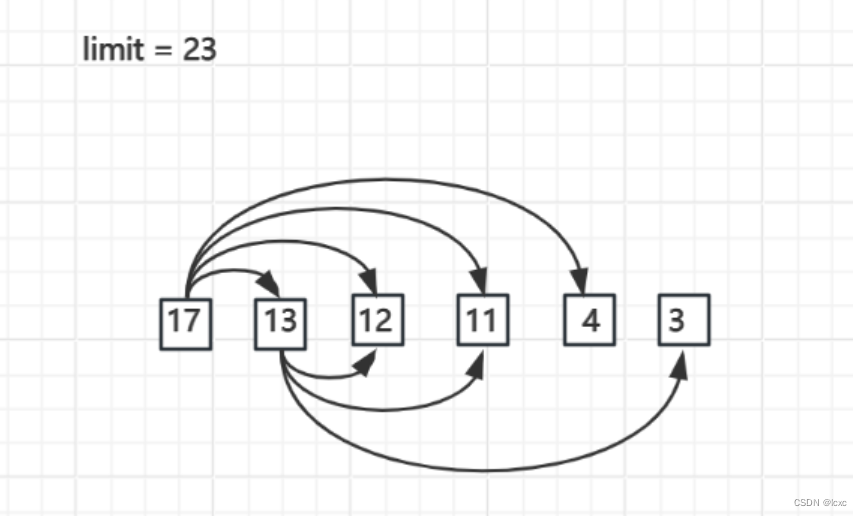
2. 让最重的那个与后面的所有书逐个比较，看看它能与后面的哪本书结合，放到一个书包里面。
（这样就能够保证最重的和较重的先被放进书包，后面轻的就更不在话下了！）

class Solution1 {
public:int GetBagNum(int bagLimit, vector<int> &books) {sort(books.begin(), books.end(), greater<>());vector<bool> inBags(books.size(), false); // 表示当前的书是否被装入书包了。int bagNum = 0;for (int i = books.size() - 1; i >= 0; i--) {if (inBags[i]) {    // 表示已经被装入书包continue;}for (int j = i - 1; j >= 0; j --) {if (!inBags[j] && books[i] + books[j] <= bagLimit) {    // 表示 i 和 j 可以装入同一个书包inBags[i] = true;inBags[j] = true;bagNum ++;break;}}if (!inBags[i]) { // 表示无法与后面的所有书一起放进书包，只能自己单独放bagNum ++;}}return bagNum;}
};

明显，出现O(n²)的算法是无法跑过所有用例的。

所以，我们要想出个办法，如何才能化简掉没有必要的比较操作呢？

仔细一看，还真的难想出来。因为感觉每一次比较都是必要的，要不然没法让较大的两本书放进书包。

从开头想，没办法化简，那就从尾想

从开头想（正向）：正是上面的正向暴力法（让两个大的先放进去）

从末尾想（方向）：让最大的跟最小的先放进去。

双指针法

让最大的和最小的结合。（因为对最小的来说，最极限的情况就是和最大相结合。也就说，对最小的书来说，它非常贪心，老是想和最大的书结合放进书包。）

方法：

先倒序；
左指针向右遍历，右指针向左遍历。

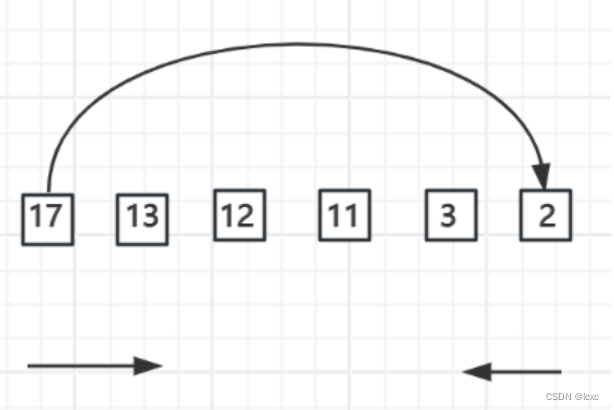
class Solution2 {
public:int GetBagNum(int bagLimit, vector<int> &books) {sort(books.begin(), books.end(), greater<>());int left = 0;int right = books.size() - 1;int bagNum = 0;while (left < right) {if (books[left] + books[right] <= bagLimit) {// 这两本放到一起bagNum ++;left ++;right --;} else {// 左边的那本单独放left ++;bagNum ++;}}return bagNum;}
};

这样，就将时间复杂度降到了O(n)。可以通过所有用例了！

思维拓展：

假如题目变种为：

现在有一种书包，这种书包只有两个槽位（即最多只能放下两件物品。），并且一个这种书包只能装下N千克的物品。现在有两种物品，一种物品A，一种物品B。一个书包内【不能放两个物品A】，但是【可以放一个A、一个B】或者【直接放两个物品B】。给你两个数组，数组1为物品A的重量数组；数组2为物品B的重量数组。数组元素是每个物品的重量（千克）。问：完全装下这堆物品，需要多少个书包？

明显这道题也是双指针就能解决。
class Solution3 {
public:int GetBagNum(int bagLimit, vector<int> &booksA, vector<int> &booksB) {sort(booksA.begin(), booksA.end()); // 升序排列sort(booksB.begin(), booksB.end(), greater<>()); // 降序排列
// 对于轻的A来说，它的贪心就是和最大的B结合放进书包int leftA = 0;int leftB = 0;int bagNum = 0;vector<bool> BInBag(booksB.size(), false); // 表示B物品是否被装进书包while (leftA < booksA.size() && leftB < booksB.size()) {if (booksA[leftA] + booksB[leftB] <= bagLimit) {BInBag[leftB] = true;bagNum ++;leftA ++;leftB ++;} else {leftB ++;}}bagNum += (booksA.size() - leftA); // 剩余的A物品是没法和物品B的结合的，只能单独装入书包。// 以下让剩余没装入的B使用双指针继续装入。int left = 0;int right = booksB.size() - 1;while (left < right) {if (booksB[left]) { // 跳过已经被装入的left ++;   continue;} if (booksB[right]) {    // 跳过已经被装入的right --;continue;}if (booksB[left] + booksB[right] <= bagLimit) {// 这两个放到一起bagNum ++;left ++;right --;} else {// 左边的那个单独放left ++;bagNum ++;}}
return bagNum;}
};

贪心+小根堆

假如我们还是坚持要用原来那种贪心：总是让两个大的先结合。

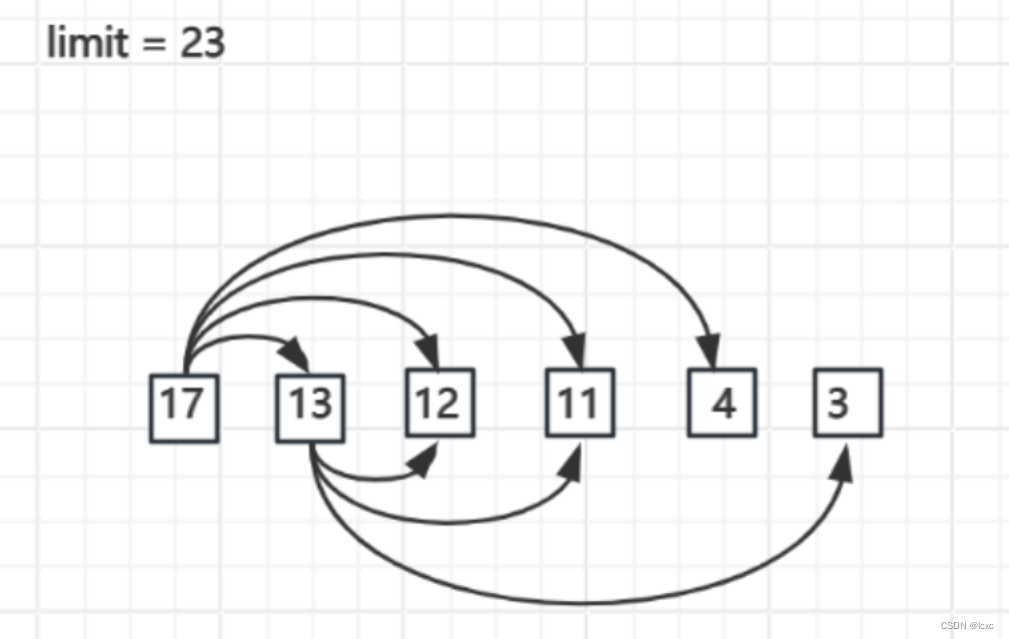
从头想过了，无法化简；从尾想过了，还好，时间复杂度下降了；还有一个地方，可以从中间想

我们再来继续仔细看看这张图，对于11来说，它既得跟17相加比较一把，还得跟13相加比较一把。有没有一种可能？让11直接跟13相加比较一把，发现不行——> 那么可以直接得出结论：11跟17是没法结合的。（因为17比13大）

也就是说，我们可以把17和13这些比较大的书转到一个容器里面，让容器里面最小的跟11相加比较，如果可以，那就装入书包；如果不行，11和容器里面的每一个都不能相结合（因为11已经和容器里面最小的相结合比较过了）

可以获取到最小元素的容器，那就只有小根堆了

但是我们要怎么把书装进小根堆呢？（什么情况装进去？）

很明显，当我们遍历到一本书，并且此书没法和堆顶元素相结合的时候，就要将其加进小根堆了。（加进小根堆，看看后续的遍历元素有没有可能再和当前的书）

class Solution {
public:int GetBagNum(int bagLimit, vector<int> &books) {sort(books.begin(), books.end(), greater<>());
priority_queue<int, vector<int>, greater<>> bigBook;
int ret = 0;
for (auto &cur: books) {if (bigBook.empty() || bigBook.top() + cur > bagLimit) {    // 没法和最小的堆顶元素结合，那就加入堆。bigBook.push(cur);} else {bigBook.pop();  // 如果可以和堆顶元素结合，那就将堆顶元素弹出来让其与当前元素结合。ret ++;}}return ret + bigBook.size();    // 剩余在堆里面的，都是没法和其他元素结合的。}
};

一个疑问：为什么和堆顶元素结合就直接结合了？为什么不和堆里面的其他元素再比较一下，看看有没有可能和更大的元素结合？

答案：没必要，数组后面还有更小的元素，更小的元素会和堆内其他元素结合的。

思维拓展：

假如题目变成这样：

现在有一种书包，这种书包只有3个书槽（即最多只能放下3本书。），并且一个这种书包只能装下N千克的书。现在有一个数组，数组元素是每本书的重量（千克）。问：完全装下这堆书，需要多少个书包？

题目如下，核心思想是一致的。都是先跟大的里面的小的比。（通过维护两个堆来完成这一功能）

class Solution4 {
public:int GetBagNum(int bagLimit, vector<int> &books) {sort(books.begin(), books.end(), greater<>());
priority_queue<int, vector<int>, greater<>> pq1Book;    // 代表只有1本书的小根堆
priority_queue<int, vector<int>, greater<>> pq2Book;    // 代表2本书的和的小根堆
int ret = 0;
for (auto &cur: books) {if (pq2Book.empty()) {if (pq1Book.empty()) {pq1Book.push(cur);} else {if (cur + pq1Book.top() <= bagLimit) {// 也就是说这两本书能够结合，能结合就放到堆2放着。int cur_top = pq1Book.top();pq1Book.pop();int sum = cur_top + cur;pq2Book.push(sum);} else {// 如果不能结合，就分开，都放到堆1pq1Book.push(cur);}}} else {if (cur + pq2Book.top() <= bagLimit) { // 直接和堆2顶的两本书结合。ret ++;pq2Book.pop();} else {    // 没法和堆2顶的任意两本书结合，只能到堆1碰碰运气if (cur + pq1Book.top() <= bagLimit) {// 也就是说这两本书能够结合，能结合就放到堆2放着。int cur_top = pq1Book.top();pq1Book.pop();int sum = cur_top + cur;pq2Book.push(sum);} else {// 如果不能结合，就分开，放到堆1pq1Book.push(cur);}}}}// 剩余的两个堆里面的书都是没法相互结合的。前面已经判断过了。return ret + pq2Book.size() + pq1Book.size();}
};