【二叉树】常见题目解析（2）-编程知识

题目1：104. 二叉树的最大深度 - 力扣（LeetCode）

题目1描述：

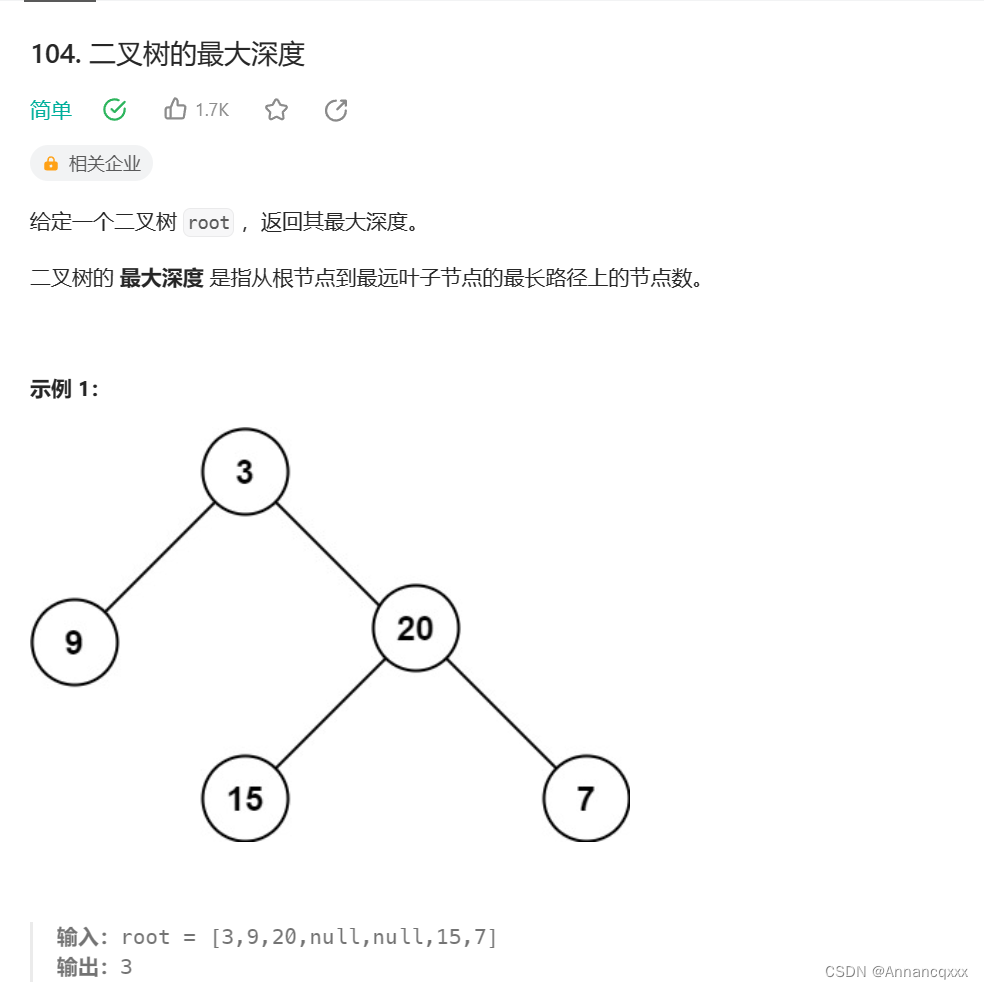
题目1分析及解决：

（1）base case：当前节点为null时，以当前节点为根节点的树最大深度是0。

（2）节点不为null时，节点应该统计左右子树的最大深度，并在其中取一个最大值 + 1即可得到以当前节点为根节点的树最大深度是多少（+ 1是因为当前节点也算一个深度）。

（3）既然要用到左右子树的递归结果，那么肯定是后序遍历整颗树。

Code：

class Solution {public int maxDepth(TreeNode root) {//空树最大深度为0if(root == null)return 0;//获取左右子树的最大深度int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);//在左右子树的结果中选一个较大值 + 1(当前节点也算一个深度)return Math.max(leftDepth,rightDepth) + 1;}
}

题目2：111. 二叉树的最小深度 - 力扣（LeetCode）

题目2描述：

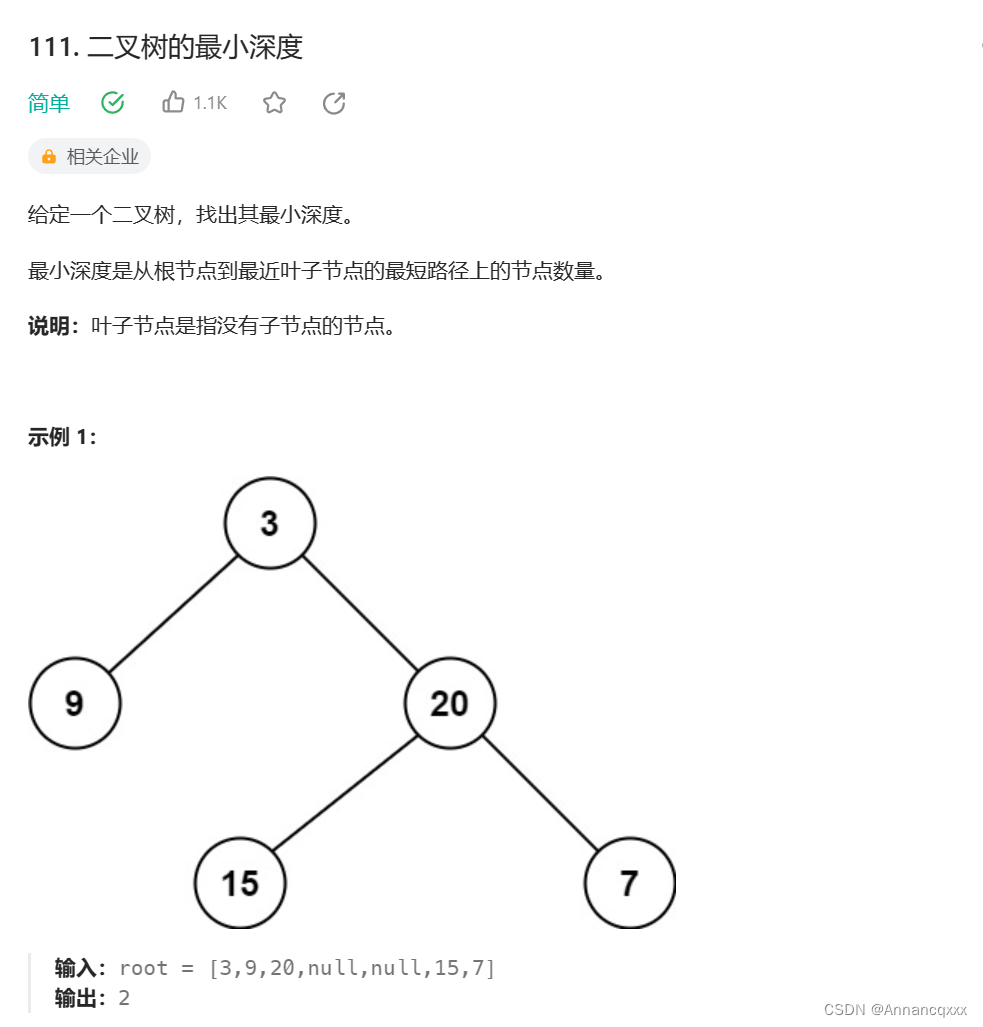
题目2分析与解决：

（1）base case：当前节点为null时，最小深度是0；当节点的左、右子节点都为null时，说明当前节点是叶子节点，最小深度是1.

（2）节点不为null时，如果当前节点的左节点不为null，就获取左节点的最小深度；如果当前节点的右节点不为null，就获取右节点的最小深度；最后在左、右子节点返回的结果中选一个较小值 + 1即可得到以当前节点为根节点的树最小深度是多少。

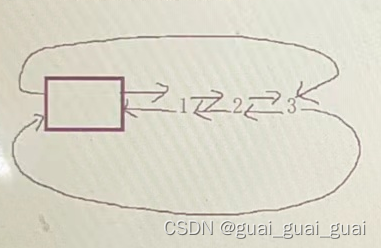
（3）由于还是要获取左、右子节点的返回结果，所以仍然是后序遍历。为什么要在左、右子节点不为null时，才能去递归获取他们的最小深度呢？看下图

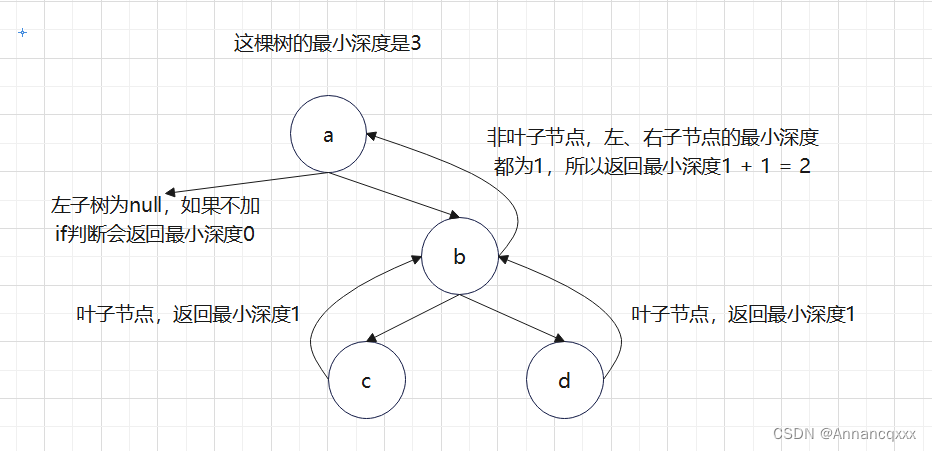
总结：不加if判断会被空节点影响最终结果。

Code：

class Solution {public int minDepth(TreeNode root) {//节点为null时，最小深度是0if(root == null)return 0;//节点为叶子节点时，最小深度是1if(root.left == null && root.right == null)return 1;int leftDepth = Integer.MAX_VALUE;int rightDepth = Integer.MAX_VALUE;if(root.left != null)leftDepth = minDepth(root.left);if(root.right != null)rightDepth = minDepth(root.right);return Math.min(leftDepth,rightDepth) + 1;}
}

题目3：958. 二叉树的完全性检验 - 力扣（LeetCode）

题目3描述：

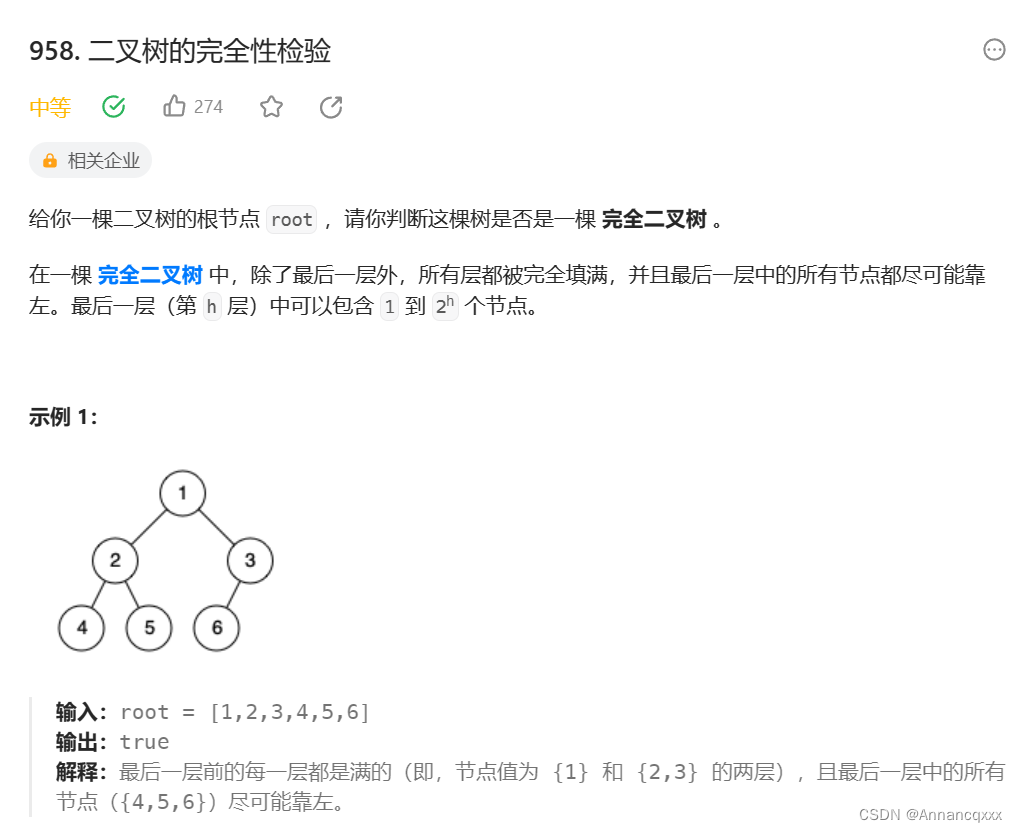
题目3分析与解决：

（1）完全二叉树的特点如下图所示：

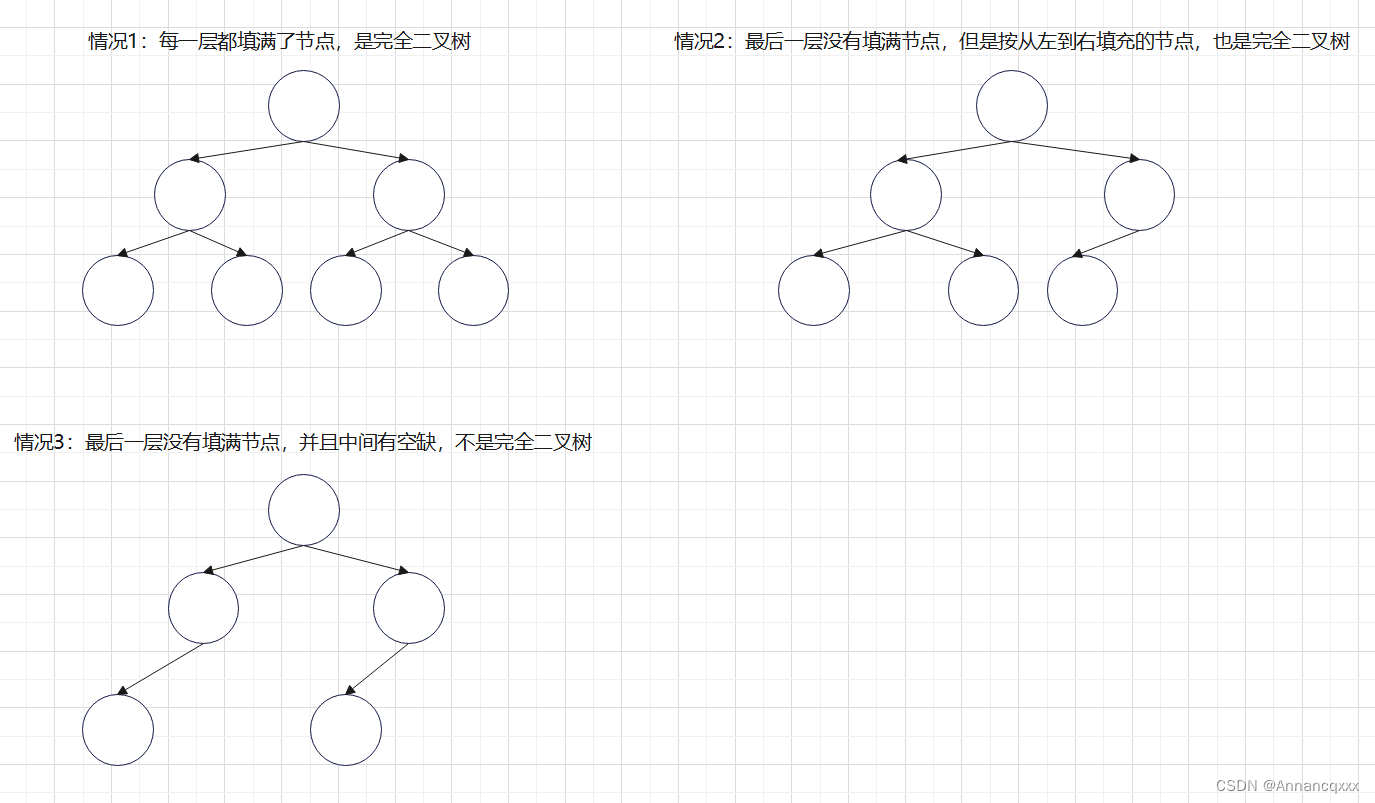
（2）逐层遍历每一个节点（bfs），当一个节点的左子节点为null而右子节点不为null时，说明不是完全二叉树。

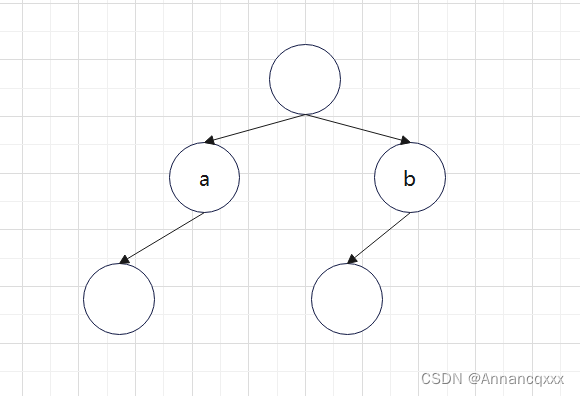
（3）当遍历到一个节点，它的左、右子结点有一个为null，若后续节点不是叶子节点，说明不是完全二叉树。如下图所示，遍历到a节点时，其左子节点不为null、右子节点为null；后面遍历b节点时，如果b是叶子节点，则不破坏完全二叉树的性质，如果b不是叶子节点，则中间有空缺，不符合完全二叉树的定义。

Code：

class Solution {//题目规定节点个数在100以内public static int MAX = 101;    //用数组模拟队列public static TreeNode [] queue = new TreeNode[MAX];//用head、tail两个变量维护队列的长度及出入队顺序public static int head,tail;public boolean isCompleteTree(TreeNode root) {//空树也是完全二叉树if(root == null)return true;//初始队列大小为0head = tail = 0;//根节点入队queue[tail++] = root;//标记变量：遍历到一个节点，只要它的左、右子节点有一个为null，就设置为trueboolean flag = false;//队列不为空while(head < tail){//弹出队头节点TreeNode node = queue[head++];//返回false的两个条件，满足一个即可//1.左子节点为null的同时右子节点不为null//2.有节点设置flag为true的同时当前节点不是叶子节点if((node.left == null && node.right != null) ||(flag && (node.left != null || node.right != null)))return false;if(node.left != null)queue[tail++] = node.left;if(node.right != null)queue[tail++] = node.right;if(node.left == null || node.right == null)flag = true;}//如果逐层遍历过程中没有返回false，那么这棵树是完全二叉树，返回truereturn true;}
}

题目4：222. 完全二叉树的节点个数 - 力扣（LeetCode）

题目4描述：

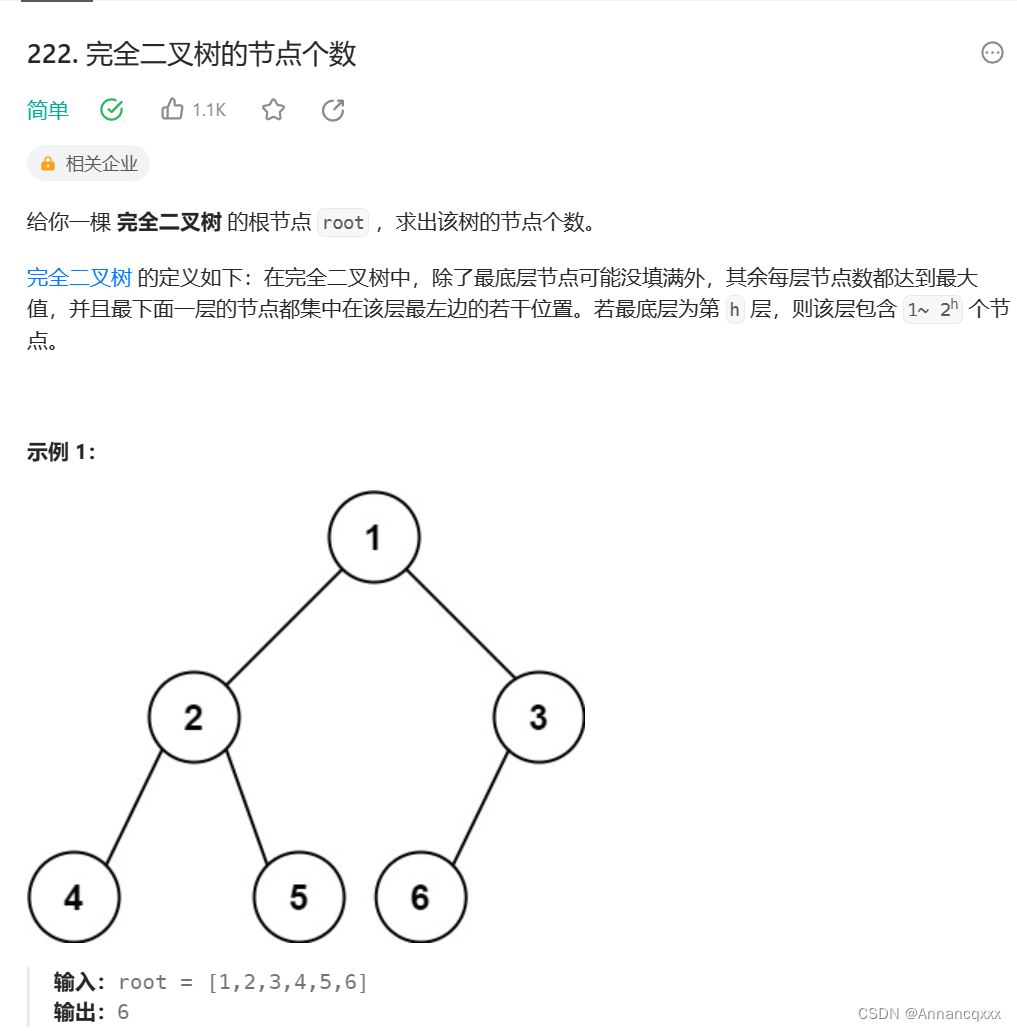
题目4分析与解决：

（1）最基本的思路是：递归左、右子树获取他们的节点个数，当递归到叶子节点时，就返回1（叶子节点的左、右子节点都为null），每层节点收集左、右子树的递归结果再 + 1（当前结点也算一个结点）返回即可。

（2）基于上述思路无论是什么类型的二叉树都能统计其结点个数，但题目强调了是一颗完全二叉树，我们该如何利用这一性质？根据题目3我们知道，一颗完全二叉树不一定是一颗满二叉树，但它一部分的子树一定是一颗满二叉树；利用这一性质，当我们发现以当前结点为根节点的树是满二叉树时，直接计算结点个数返回，无需获取左、右子树的递归结果，减少时间复杂度。

（3）一颗满二叉树的结点个数如何计算呢？不就是2^层数 - 1吗？所以当我们递归到一个结点时，我们首先判断它是否是一颗满二叉树，是则直接计算结点个数；不是，则递归左、右子树，获取左、右子树的递归结果，再+1即可。

Code：

class Solution {public int countNodes(TreeNode root) {//空结点肯定不算一个结点if(root == null)return 0;TreeNode l = root.left;int leftDepth = 0;//一直往左树遍历，看最深是多少while(l != null){l = l.left;leftDepth++;}TreeNode r = root.right;int rightDepth = 0;//一直往右树遍历，看最深是多少while(r != null){r = r.right;rightDepth++;}//如果左、右子树的深度相同//说明以当前结点为根节点的树是一颗满二叉树，直接计算结点个数并返回if(leftDepth == rightDepth)return (2 << leftDepth) - 1;else//否则获取左、右子树的递归结果 + 1 返回return countNodes(root.left) + countNodes(root.right) + 1;}
}