系列文章目录

---

---

前言

模型参考自适应控制模块计算控制动作，使不确定的受控系统跟踪给定参考被控对象模型的行为。使用该程序块，可以实现以下模型参考自适应控制 (MRAC) 算法。

• 直接 MRAC - 根据被控对象与参考工厂模型状态之间的实时跟踪误差，估算反馈和前馈控制器增益。

• 间接 MRAC - 根据参考设备模型与估计系统状态之间的跟踪误差，估计被控对象系统的参数。然后，根据估计系统和参考模型的参数推导出反馈和前馈控制器增益。

直接和间接 MRAC 还能估算被控系统的外部干扰和不确定性模型。然后，控制器在计算控制动作时使用该模型对干扰和不确定性进行补偿。

在这两种情况下，控制器都会根据跟踪误差实时更新估计参数和干扰模型。

---

一、参考模型

对于直接和间接 MRAC 而言，以下参考被控对象模型是理想的系统，它描述了您在实践中想要实现的理想行为。
$${\dot{x}}_m(t)=A_m{x}_m(t)+B_{m}r(t)$$
此处

• r(t) 是外部参考信号。

• xm(t) 是被控对象模型的状态。由于 r(t) 已知，因此可以通过模拟参考模型得到 xm(t)。

• Am 是恒定状态矩阵。对于一个稳定的参考模型，Am 必须是一个 Hurwitz 矩阵，其每个特征值都必须是严格的负实部。

• Bm 是控制有效矩阵。

二、扰动与不确定性模型

模型参考自适应控制模块维护着受控系统中干扰和模型不确定性的内部模型 $u_{ad}$。
$$u_{ad}=w^T\varphi (x)$$
w 是控制器根据跟踪误差实时更新的自适应控制权重向量。

要定义 ϕ(x)，可以使用以下特征定义之一。

• 被控对象的状态向量 - 这种方法可能无法充分反映系统的不确定性。在不了解干扰和模型不确定性的复杂性时，使用状态作为特征可能是一个有用的起点。

• 高斯径向基函数 - 当扰动和模型的不确定性是非线性的，且扰动模型的结构未知时，请使用此选项。径向基函数要求事先了解模型的运行域，这在某些情况下可能比较困难。

• 单隐层神经网络 - 当扰动和模型的不确定性是非线性的，扰动模型的结构未知，并且您没有运行域的先验知识时，请使用此选项。神经网络是一种通用函数近似器，可以近似任何连续函数。

• 提供给控制器模块的外部源 - 使用该选项可自定义特征向量。如果您知道干扰和不确定性模型的结构，则可以使用该选项。例如，您可以使用自定义特征向量来确定特定的未知被控对象参数。

三、直接 MRAC

直接 MRAC 控制器的控制结构如下

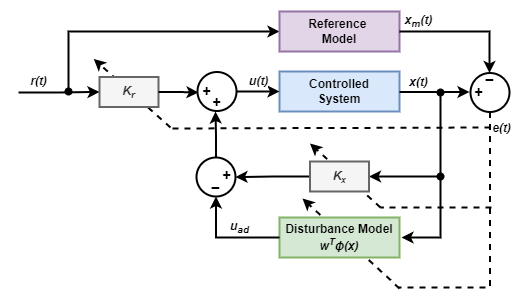
控制器计算控制输入 u(t) 的方法如下
$$\begin{array}{c}u(t)=k_{x}x(t)+k_{r}r(t)-u_{ad}\\ u_{ad}=w^T\varphi (x)\end{array}$$

此处

• x(t) 是受控系统的状态。

• r(t) 是外部参考信号。

• kx 和 kr 分别是反馈和前馈控制器增益。

• $u_{ad}$ 是根据扰动模型得出的自适应控制分量。
  $\varphi (x)$ 包含干扰模型特征。

• w 是自适应扰动模型权重向量。

• V 是隐藏层权重向量。

对于单隐层神经网络，$u_{ad}$ 为
$$u_{ad}=w^T\sigma (V^{T}x)$$
此处

• V 是隐层权重向量。

• σ 是 sigmoid 激活函数。

控制器计算受控系统状态与参考模型状态之间的误差 e(t)。然后利用该误差实时调整 kx、kr 和 w 的值。

名义模型

受控系统通常具有建模不确定性和外部干扰，其标称状态方程如下。控制器在更新控制器参数时，会使用这一预期的标称被控对象行为。
$$\dot{x}(t)=Ax(t)+B(u(t)+f(x))$$
这里的

• x(t) 是要控制系统的状态。

• u(t) 是控制输入。

• A 是恒定的状态转换矩阵。

• B 是恒定的控制有效矩阵。

• f(x) 是系统中匹配的不确定性。

参数更新

直接 MRAC 控制器使用以下公式更新状态矢量、径向基函数和外部源特征定义的控制器增益和干扰模型权重
$$\begin{array}{l}{\dot{k}}_x={\Gamma }_{x}x(t)e^T(t)PB\\ {\dot{k}}_r={\Gamma }_{r}r(t)e^T(t)PB\\ \dot{w}={\Gamma }_w\varphi (x)e^T(t)PB\end{array}$$
单隐层干扰模型更新方程使用相同的控制器增益更新和以下更新方程。
$$\begin{array}{l}\dot{w}=-(\sigma (V^{T}x)-{\sigma }^{\prime }(V^{T}x)V^{T}x)e^T(t)PB{\Gamma }_w\\ \dot{V}=-\Gamma Vx{e}^T(t)PB{w}^T\sigma (V^{T}x)\end{array}$$

Here, P is the solution to the following Lyapunov function based on the reference model state matrix and B is the control effective matrix from the nominal plant model.
$$A_m^{T}P+P{A}_m+Q=0$$
这里，Q 是大小为 N 乘 N 的正定矩阵，其中 N 是状态向量 x(t) 的大小

间接 MRAC

间接 MRAC 控制器的控制结构如下。参考模型为

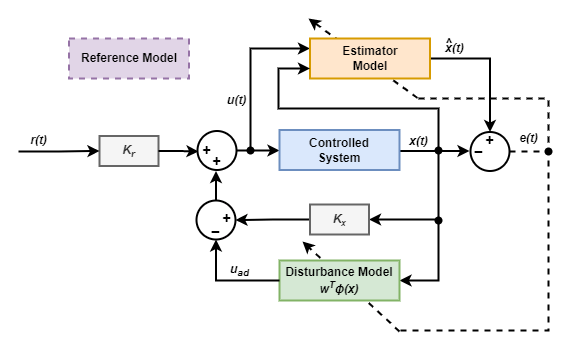
控制器计算控制输入 u(t) 的方法如下
$$\begin{array}{c}u(t)=k_{x}x(t)+k_{r}r(t)-u_{ad}\\ u_{ad}=w^T\varphi (x)\end{array}$$

这里：

• $\hat{x}(t)$ 是由估计模型产生的受控系统估计状态。

• r(t) 是外部参考信号。

• kx 和 kr 分别是反馈和前馈控制器增益。

• $u_{ad}$ 是根据扰动模型得出的自适应控制分量。

• $\varphi (x)$ 包含干扰模型特征。

• w 是自适应扰动模型权重向量。

控制器计算实际系统状态和估计系统状态之间的误差 e(t)。然后利用该误差实时调整 w 的值。控制器还利用 e(t) 实时更新估计模型的参数。增益 kx 和 kr 的值来自估计模型和参考模型的参数。

估计器模型和控制器增益

间接 MRAC 控制器包含以下受控系统的估计模型。
$$\dot{\hat{x}}(t)=\hat{A}x(t)+\hat{B}u(t)$$
这里：

• $\dot{\hat{x}}(t)$ 是估计的系统状态。

• $u(t)$ 是控制输入。

• $\hat{A}$ 是估计器的状态转换矩阵。

• $\hat{B}$ 是估计器的控制有效矩阵。

在运行过程中，控制器基于估计误差 e(t)更新 $\hat{A}$ 和 $\hat{B}$ 。

间接 MRAC 控制器不直接估算控制器增益，而是采用基于动态反演的方法，从参考模型和估算模型的参数中推导出反馈增益 $k_x$ 和前馈增益 $k_r$，具体如下。
$$\begin{array}{c}{k}_r=\frac{B_m}{\hat{B}}\\ k_x=\frac{1}{\hat{B}}\left(A_m-\hat{A}\right)\end{array}$$
这里，$\frac{1}{\hat{B}}$ 是矩阵 $\hat{B}$ 的 Moore-Penrose 摩尔-彭罗斯伪逆。

参数更新

间接 MRAC 控制器使用以下公式更新状态矢量、径向基函数和外部源特征定义的估计模型参数和干扰模型权重
$$\begin{array}{l}\dot{\hat{A}}={\Gamma }_{a}x(t)e^T(t)P\\ \dot{\hat{B}}={\Gamma }_{bu(t)}{e}^T(t)P\\ \dot{w}={\Gamma }_w\varphi (x)e^T(t)PB\end{array}$$
单隐层干扰模型更新方程使用相同的估计模型参数更新和以下更新方程。
$$\begin{array}{l}\dot{w}=-(\sigma (V^{T}x)-{\sigma }^{\prime }(V^{T}x)V^{T}x)e^T(t)PB{\Gamma }_w\\ \dot{V}=-\Gamma Vx{e}^T(t)PB{w}^T\sigma (V^{T}x)\end{array}$$
这里，P 是以下 Lyapunov 函数的解。
$$k_{\tau }^{T}P+P{k}_{\tau }+Q=0$$

kτ 是估计器反馈增益。默认情况下，该值与参考模型状态转换矩阵 Am 相对应。不过，也可以指定不同的估计器反馈增益值。

学习修正

对于直接和间接 MRAC，为了在更高的学习率下增加稳健性，可以修改参数更新，加入一个可选的动量项。您可以从两种可能的学习修改方法中选择一种：sigma 和 e-modification。

对于西格玛修正，每次参数更新的动量项都是动量权重参数 σ 与当前参数值的乘积。例如，以下直接 MRAC 控制器的更新方程就包含了 σ 修正项。
$$\begin{array}{l}{\dot{k}}_x={\Gamma }_{x}x(t)e^T(t)PB+\sigma k_x\\ {\dot{k}}_r={\Gamma }_{r}r(t)e^T(t)PB+\sigma k_x\\ {\dot{w}}_x={\Gamma }_w\varphi (t)e^T(t)PB+\sigma w\end{array}$$
对于 e-修正，控制器通过误差矢量的规范对 sigma-修正动量项进行缩放。例如，以下间接 MRAC 控制器的更新方程就包含了一个 e 修正项。
$$\begin{array}{l}\dot{\hat{A}}={\Gamma }_{a}x(t)e^T(t)P+\sigma |e(t)|\hat{A}\\ \dot{\hat{B}}={\Gamma }_{b}u(t)e^T(t)P+\sigma |e(t)|\hat{B}\\ {\dot{w}}_x={\Gamma }_w\varphi (t)e^T(t)PB+\sigma |e(t)|w\end{array}$$
要调整这两种方法的学习修正量，可改变动量权重参数 σ 的值。

参考文献

[1] Ioannou, Petros A., and Jing Sun. Robust adaptive control, Courier Corporation, 2012.

[2] Narendra, Kumpati S, and Anuradha M Annaswamy. Stable Adaptive Systems. Courier Corporation, 2012.

[3] Narendra, Kumpati S., and Anuradha M. Annaswamy. “Robust Adaptive Control.” In 1984 American Control Conference, 333–35. San Diego, CA, USA: IEEE, 1984. https://doi.org/10.23919/ACC.1984.4788398