​

一、近似表达方式

  插值、拟合和投影都是常用的近似表达方式，用于对数据或函数进行估计、预测或表示。

1. 插值（Interpolation）

  指通过已知数据点之间的插值方法，来估计或推算出在这些数据点之间的数值。插值可以用于构建平滑的曲线或曲面，以便在数据点之间进行预测或补充缺失的数据。

2. 拟合（Fitting）

  指通过选择合适的函数形式和参数，将一个数学模型与已知数据点拟合得最好的过程。拟合的目标是找到一个函数，使其在数据点附近的值与实际观测值尽可能接近。拟合可以用于数据分析、曲线拟合、回归分析等领域。

3. 投影（Projection）

  指将一个向量或一组向量映射到另一个向量空间或子空间上的过程。在线性代数中，投影可以用来找到一个向量在另一个向量或向量空间上的投影或投影分量。投影可以用于降维、数据压缩、特征提取等领域，以及计算机图形学中的投影变换。

二、Lagrange插值

   Lagrange插值是一种用于通过已知数据点构造一个多项式函数的方法，基于拉格朗日插值多项式的原理（该多项式通过每个数据点并满足相应的条件），拉格朗日插值可用于估计数据点之间的值，而不仅仅是在给定数据点上进行插值。

1. 拉格朗日插值方法

1. 拉格朗日基函数： 对于给定的插值节点 $x_0,x_1,\dots ,x_n$，拉格朗日插值使用如下的拉格朗日基函数：

   $$L_i(x)=\prod _{j=0,j\ne i}^n\frac{x-x_j}{x_i-x_j}$$

2. 插值条件： 拉格朗日插值要求插值多项式满足插值条件：对所有 $i$，$P(x_i)=y_i$

3. 插值多项式： 构造插值多项式为：$P(x)={\sum }_{i=0}^n{y}_i{L}_i(x)$

  通过这种方法，可以在给定的数据点上获得一个平滑的插值函数，使得在这些数据点之间的任何位置上都可以估计函数的值。Lagrange插值在数据点较少或数据点之间存在较大间隔时可能会出现一些问题，例如插值多项式可能会产生振荡现象，这被称为Runge现象。

2. Lagrange插值公式

$$L_i(x)=\prod _{j=0,j\ne i}^n\frac{x-x_j}{x_i-x_j}$$$$P(x)=\sum _{i=0}^n{y}_i{L}_i(x)$$

a. 线性插值（n=1）

$$P(x)=y_0\frac{(x-x_1)}{(x_0-x_1)}+y_1\frac{(x-x_0)}{(x_1-x_0)}$$

b. 抛物插值（n=2）

$$P(x)=y_0\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}+y_1\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}+y_2\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}$$

三、Newton插值

1. 天书

2. 人话

  Newton插值基于差商的概念：通过给定的一组数据点，Newton插值可以生成一个通过这些点的多项式，从而在给定的数据范围内进行插值和外推。
  Newton插值的基本思想是使用差商来递归地构建一个多项式。差商是通过递归地计算数据点之间的差分来定义的。具体而言，对于给定的数据点 $(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$，差商可以表示为：

$$f[x_0]=y_0$$$$f[x_1,x_0]=\frac{(f[x_1]-f[x_0])}{(x_1-x_0)}$$$$f[x_2,x_1,x_0]=\frac{(f[x_2,x_1]-f[x_1,x_0])}{(x_2-x_0)}$$$$\dots \dots \dots \dots$$$$f[x_n,x_{n-1},...,x_0]=\frac{(f[x_n,x_{n-1},...,x_1]-f[x_{n-1},...,x_0])}{(x_n-x_0)}$$
然后，通过将这些差分商逐步添加到多项式中，可以得到一个多项式，表示为：
$P(x)=f[x_0]+f[x_1,x_0](x-x_0)+f[x_2,x_1,x_0](x-x_0)(x-x_1)+...$

  Newton插值的优点之一是它可以通过添加更多的数据点来逐步改进插值结果。然而，同Lagrange插值一样，它也存在龙格现象（Runge’s phenomenon），导致在边界处产生振荡。

3. 例题

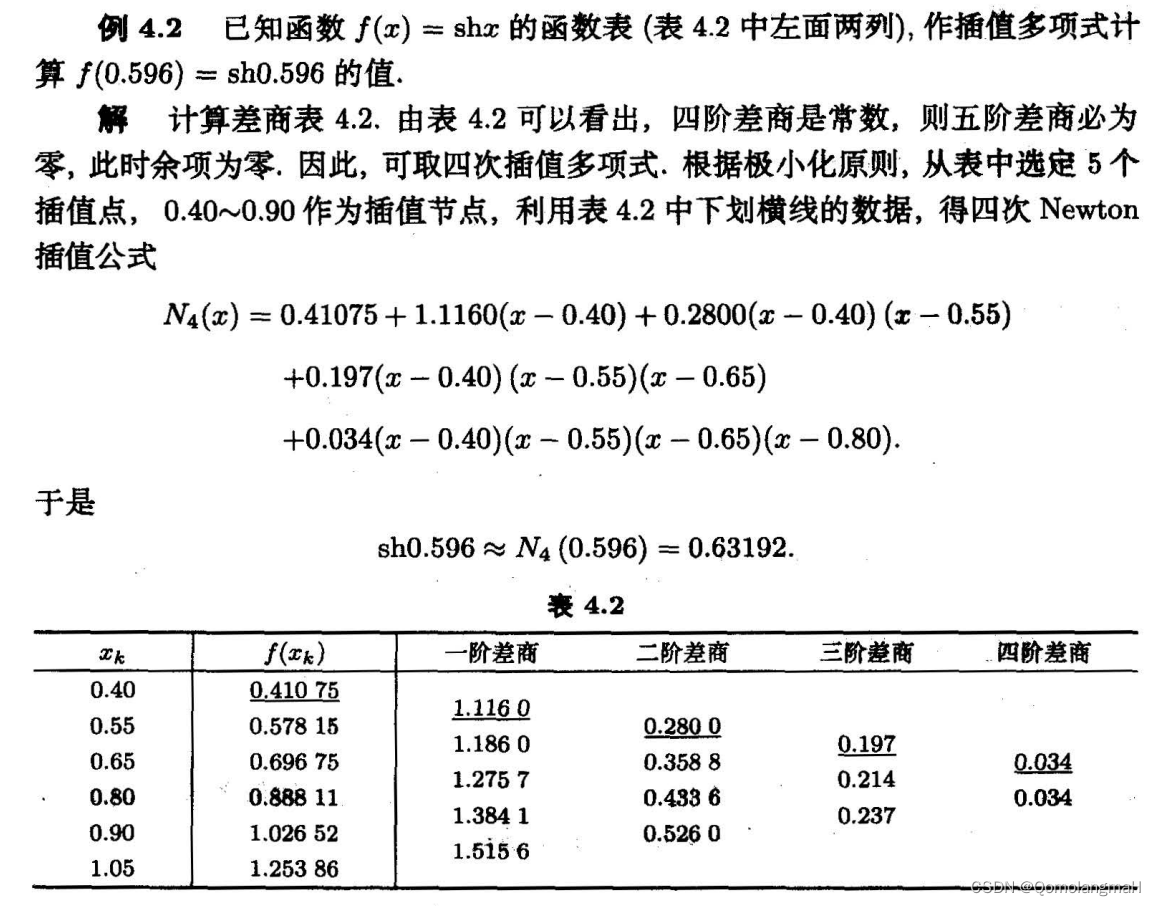
4. python实现

def newton_interpolation(x, y, xi):# 计算差分商n = len(x)f = [[0] * n for _ in range(n)]for i in range(n):f[i][0] = y[i]for j in range(1, n):for i in range(n - j):f[i][j] = (f[i + 1][j - 1] - f[i][j - 1]) / (x[i + j] - x[i])# 构建插值多项式result = f[0][0]for j in range(1, n):term = f[0][j]for i in range(j):term *= (xi - x[i])result += termreturn result# 示例数据
x = [0.32, 0.34, 0.36]
y = [0.314567, 0.333487, 0.352274]
xi = 0.3367# 进行插值
interpolated_value = newton_interpolation(x, y, xi)
print("插值结果:", interpolated_value)

输出：

插值结果: 0.3303743620375

5. C语言实现

#include <stdio.h>double newton_interpolation(double x[], double y[], int n, double xi) {// 计算差分商double f[n][n];for (int i = 0; i < n; i++) {f[i][0] = y[i];}for (int j = 1; j < n; j++) {for (int i = 0; i < n - j; i++) {f[i][j] = (f[i+1][j-1] - f[i][j-1]) / (x[i+j] - x[i]);}}// 构建插值多项式double result = f[0][0];for (int j = 1; j < n; j++) {double term = f[0][j];for (int i = 0; i < j; i++) {term *= (xi - x[i]);}result += term;}return result;
}int main() {// 示例数据double x[] = {0.32, 0.34, 0.36};double y[] = {0.314567, 0.333487, 0.352274};int n = sizeof(x) / sizeof(x[0]);double xi = 0.3367;// 进行插值double interpolated_value = newton_interpolation(x, y, n, xi);printf("插值结果: %f\n", interpolated_value);return 0;
}

输出：

插值结果: 0.330374

​

• Lagrange插值使用基于Lagrange多项式的方法来构建插值多项式.
  • Lagrange多项式是通过将每个数据点与一个基函数相乘，并使得在其他数据点上该基函数为零来构造的。最终的插值多项式是将所有这些基函数相加得到的。
  • Lagrange插值的优点是易于理解和实现，但在数据点较多时可能会导致计算复杂度较高的问题。
• Newton插值使用差商的概念来构建插值多项式。
  • 差商是一个递归定义的概念，用于计算插值多项式中的系数。差商的计算可以通过表格形式进行，其中每一列都表示不同阶数的差商，通过计算差商，可以逐步构建插值多项式。
  • Newton插值的优点是在计算差商时可以重复使用已计算的差商值，从而减少计算量。