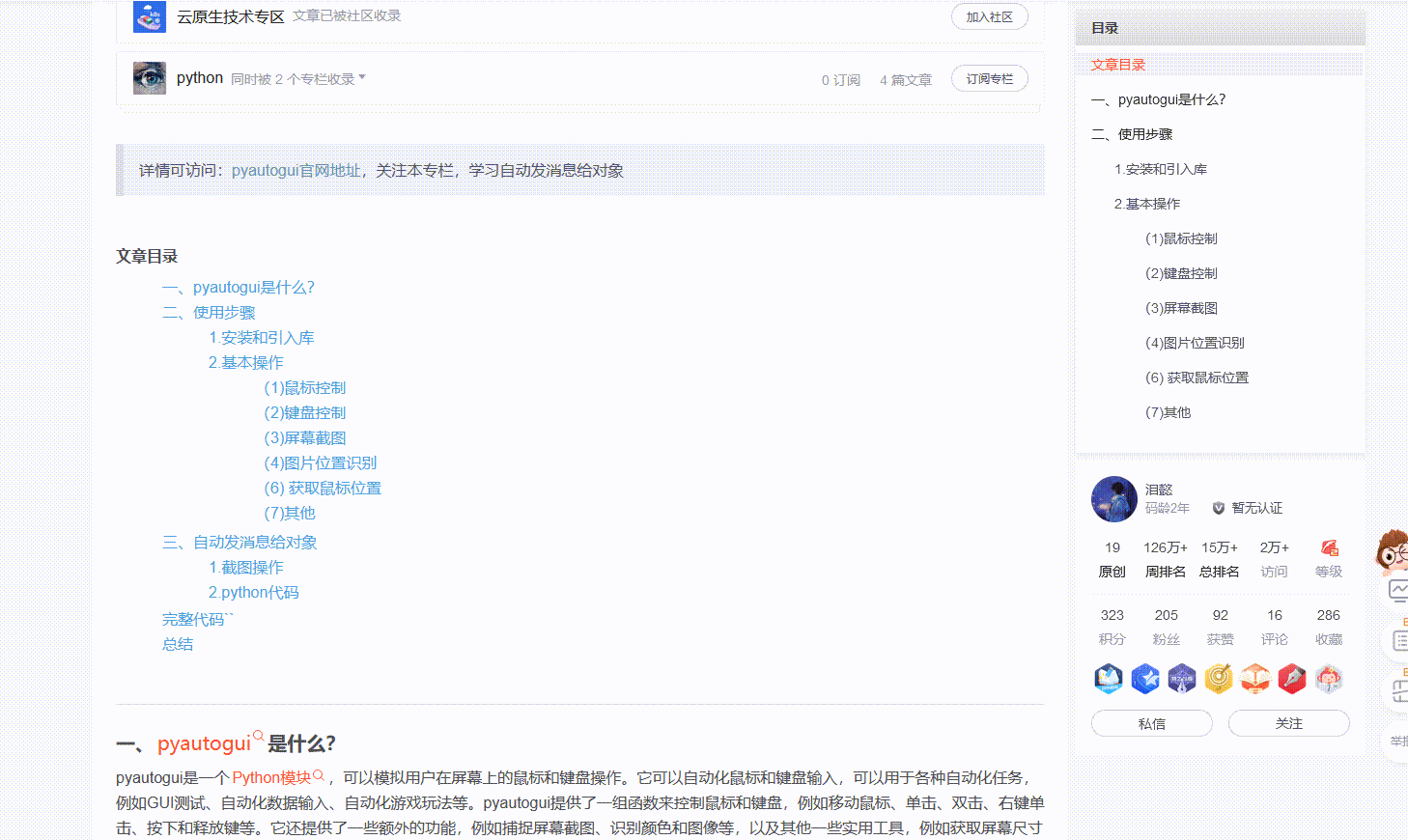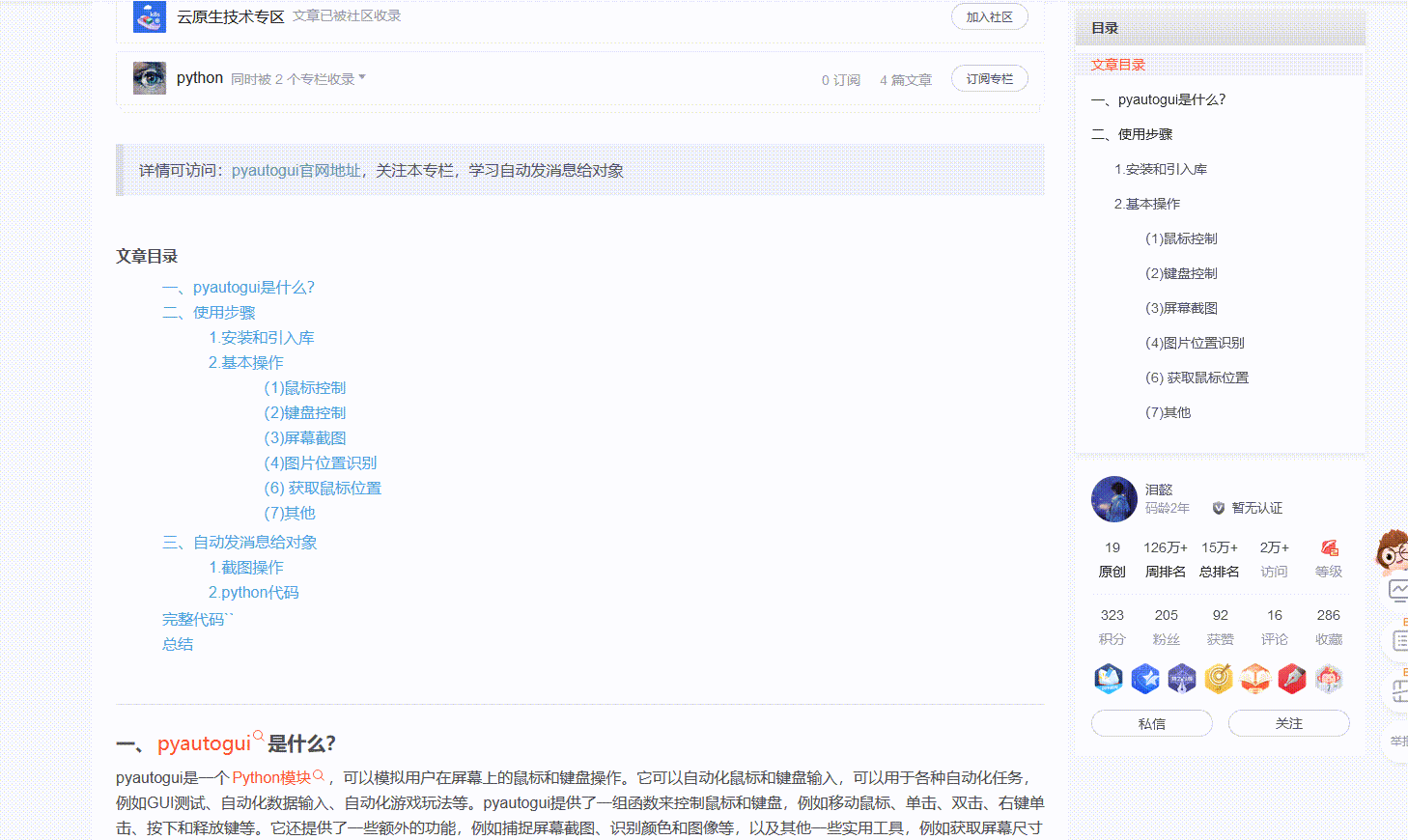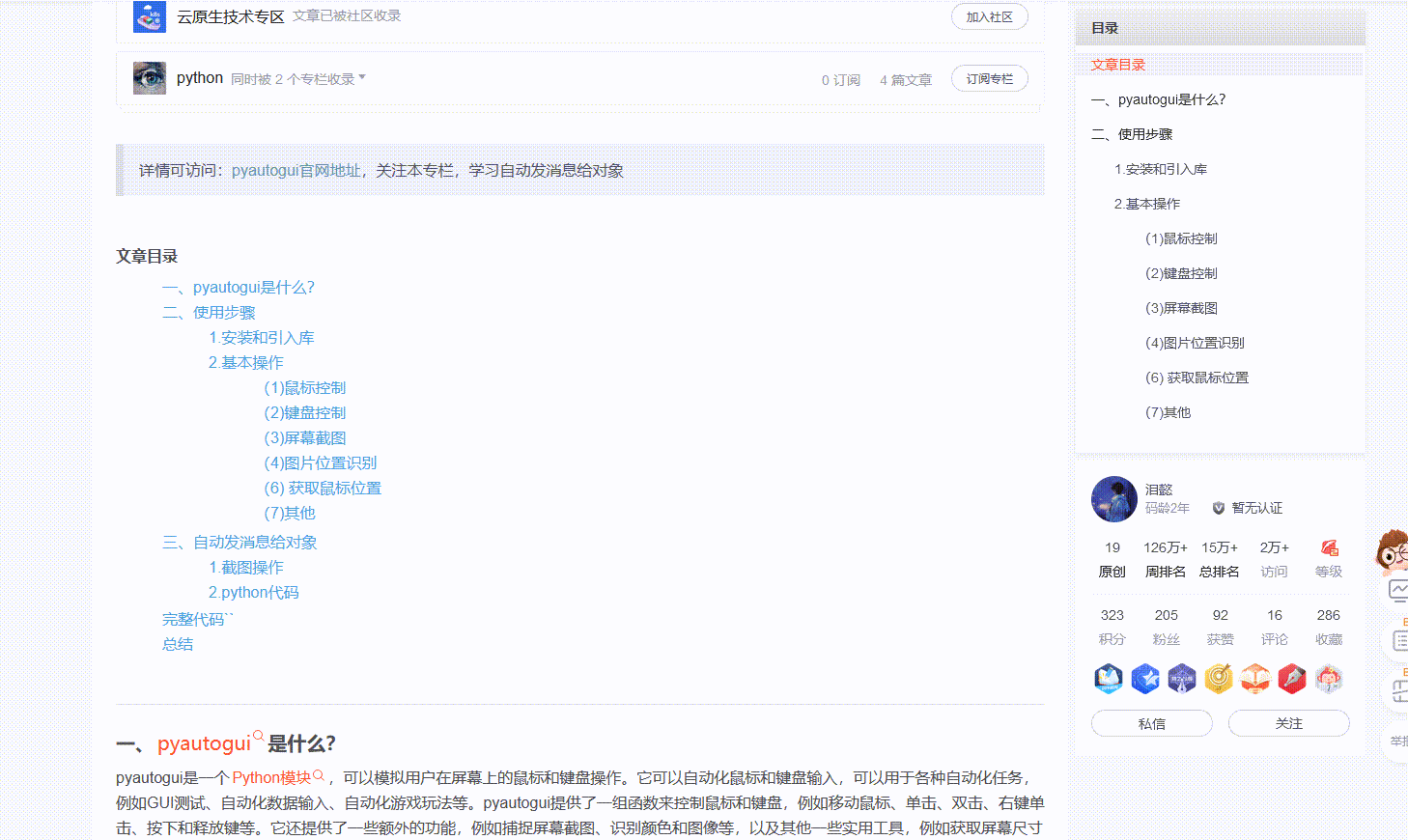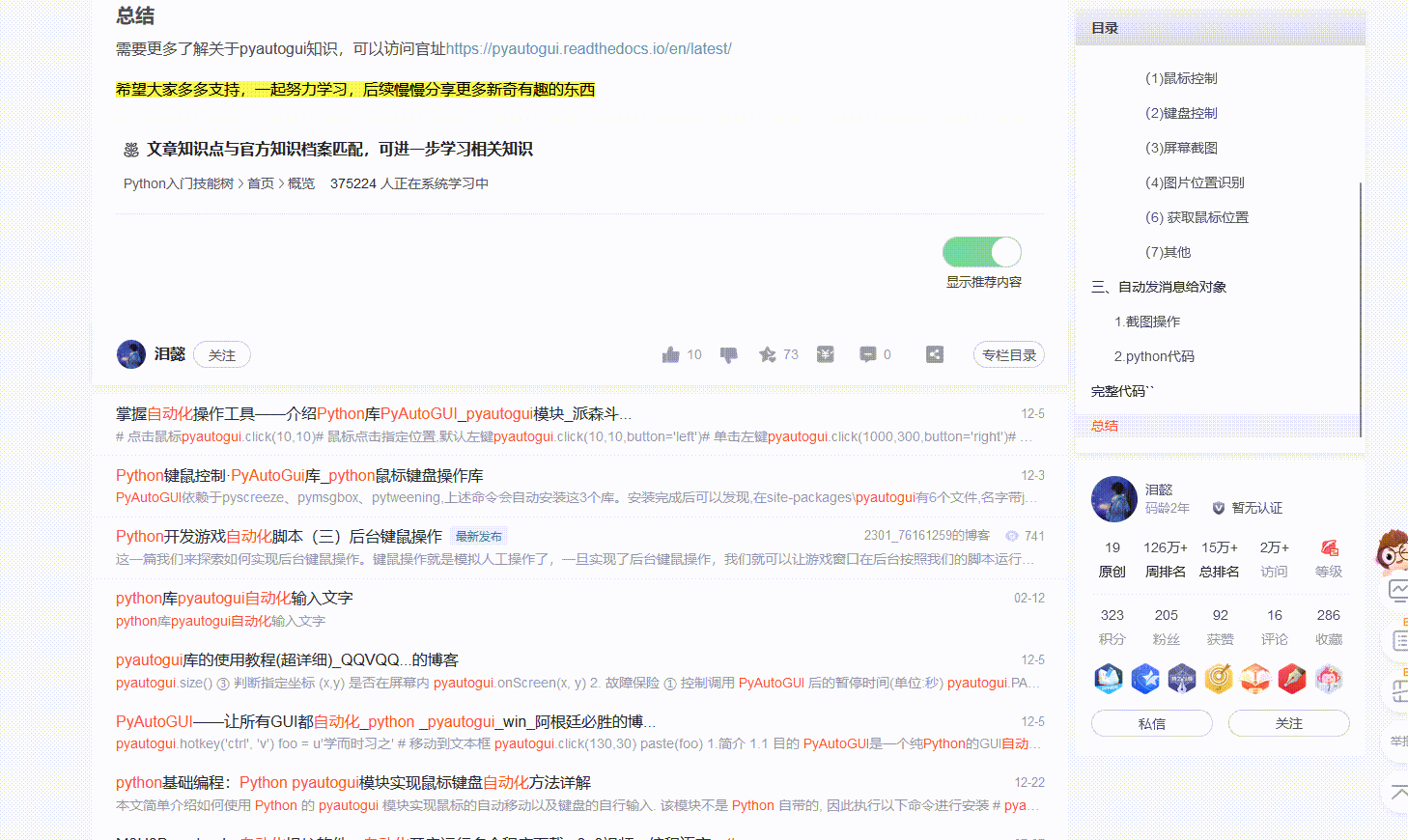
文章目录
- 上一篇
- 对偶表示
- 对偶问题的基本性质
- 对偶问题的经济学解释:影子价格
- 下一篇
上一篇
最优化理论复习–单纯形方法
对偶表示
一般情况:
对偶问题与原问题的字母表示:

对偶表示运用表格:
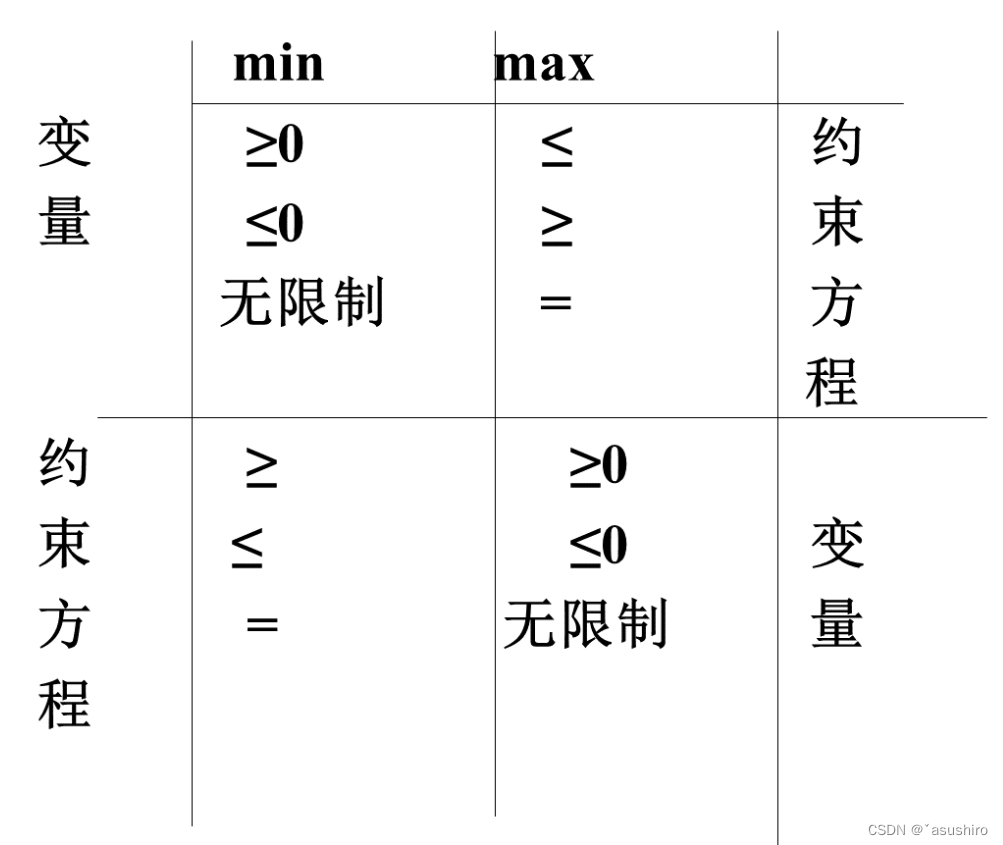
- m i n ⇒ m a x min \Rightarrow max min⇒max约束方程由变量符号取反得到,变量符号由约束方程符号直接得到
- m a x ⇒ m i n max \Rightarrow min max⇒min约束方程由变量符号直接得到,变量符号由约束方程取反得到
.


一般情况都是原问题和对偶问题的约束条件和变量之间符号的变化

对偶问题的基本性质
定义原问题表示为(L), 对偶问题表示为(D)
-
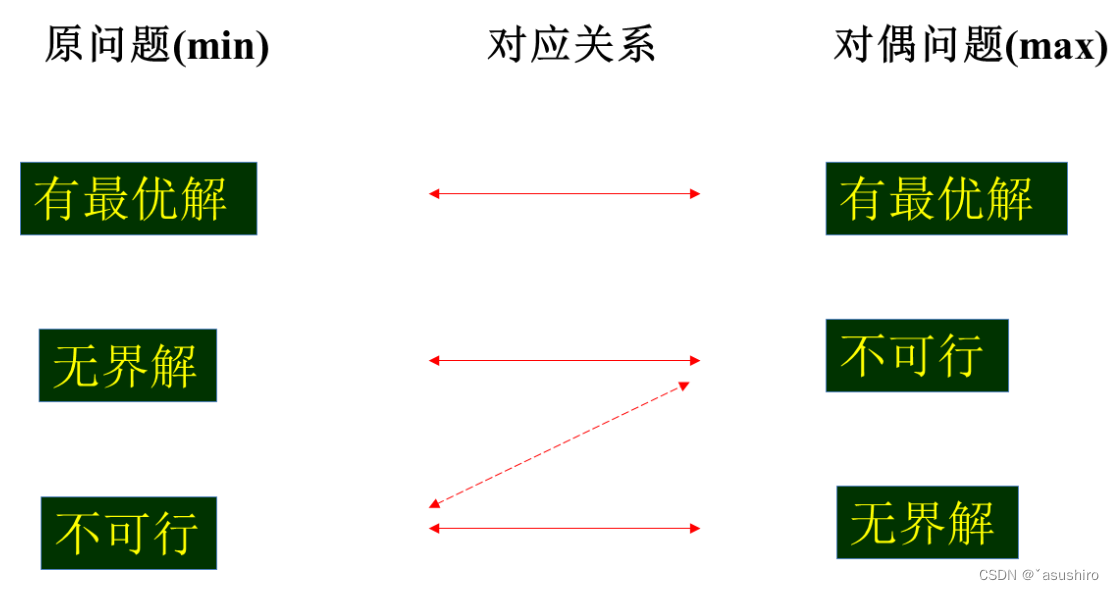
弱对偶定理
若 x ( 0 ) , w ( 0 ) x^{(0)}, w^{(0)} x(0),w(0)分别为(L), (D)的可行解,则有 c x ( 0 ) > = w ( 0 ) b cx^{(0)} >= w^{(0)}b cx(0)>=w(0)b- 即最小化问题的函数值始终大于等于对偶问题最大问题的函数值
- 也就是对偶问题的值都是原问题的下界,原问题的值是对偶问题的上界
-
最优性准则
若 x ( 0 ) , w ( 0 ) x^{(0)}, w^{(0)} x(0),w(0)分别为(L), (D)的可行解且 c x ( 0 ) = w ( 0 ) b cx^{(0)} = w^{(0)}b cx(0)=w(0)b,则 x ( 0 ) , w ( 0 ) x^{(0)}, w^{(0)} x(0),w(0)分别为(L)、(D)问题的最优解。当原问题与对偶问题的目标函数值相同时,此时的解就是原问题和对偶问题的最优解。
-
强对偶定理
若(L)、(D)均有可行解,则(L)、(D)均有最优解,且(L)、(D)的最优解目标函数值相同。
推论:
在用单纯形法求解LP问题(L)的最优单纯形表中松弛变量的检验数的相反数(单纯形乘子 w = c B B − 1 w = c_BB^{-1} w=cBB−1,单纯形表的最小面一行)就是其对偶问题的最优解。
坑点:当原问题的约束为 > = >= >=形式时,就要减一个松弛变量,因次在单纯形方法的检验数是添了一个负号的,松弛变量原本的值要去掉
当原问题达到最优时,单纯形乘子即为对偶问题最优解。

4. 互补松弛定理

(1)(2)中 c , x ( 0 ) c, x^{(0)} c,x(0)是根原问题有关系的, w ( 0 ) w(0) w(0)是根对偶问题有关系的, A是跟两个问题都有关系的
将上面的c换成b就是下面的式子
(3)(4)中 b , x ( 0 ) b, x^{(0)} b,x(0)是跟原问题有关的, w ( 0 ) , w^{(0)}, w(0),是跟对偶问题有关的,A是两个问题都有关系的
证明就是利用弱对偶定理和最优性准则建立传递关系,成为等号,移项就行。
互补松弛定理就是利用约束条件与变量之间的关系,所以在用的时候关注这两者就行,记住其中至少一项为零

对偶问题的经济学解释:影子价格
定义:影子价格是在最优配置下资源的理想价格

- 若把原问题的约束条件看成是广义的资源约束则右端项的值表示每种资源的可用量
- 对偶的经济含义:资源的单位改变量引起目标函数的增加量
- 通常称对偶解为影子价格
- 影子价格的大小客观地反映了资源在系统内的稀缺程度。资源的影子价格越高,说明资源在系统内越稀缺,而增加该资源的供应量对系统目标函数值贡献越大
影子价格是根据资源在生产中作出贡献而作出的估价,这种估价不是资源的市场价格。他反映了再最优经济结构中,在资源的到最优配置前提下,资源的边际使用价值。
而从单纯形表中松弛变量的值对应的就是经济结构中的影子价格,也可以说对偶问题的最优解向量时结构中的影子价格。
-
约束变量右边的 b i b_i bi每增加1,目标变量的值增加对偶问题的对应解 f ( x ) + y i f(x) + y_i f(x)+yi
通过影子价格可以反应这个资源的边际使用价值 -
影子价格也可以反应资源的稀缺程度
- y i > 0 y_i > 0 yi>0 表示资源短缺,影子价格越大,稀缺程度越高
- y i = 0 y_i = 0 yi=0 表示资源有剩余,不短缺
-
影子价格也可以反应资源的使用价值
- 资源占有者赋予资源的内部价格,与资源的市场价格无直接关系
- 可以计算出经济活动成本
下一篇
未完待续



![[BJDCTF2020]EzPHP 许多的特性](https://img-blog.csdnimg.cn/direct/09860d80218349dab46afb9ebe0b4784.png)