12.7图欧拉回路与路径，图的一些性质，存储方式，图的遍历（有向图无向图BFSDFS）-编程知识

欧拉回路与欧拉路径

存在条件

无向图存在欧拉回路的充要条件
一个无向图存在欧拉回路，当且仅当该图所有顶点度数都为偶数,且该图是连通图。
无向图存在欧拉路径的充要条件
当且仅当该图顶点度数为奇数的点的个数为0或者2。

欧拉定理二：
如果一个无向图有2n个奇顶点，那么它至少需要n笔画成。

有向图存在欧拉回路的充要条件
一个有向图存在欧拉回路，所有顶点的入度等于出度且该图是连通图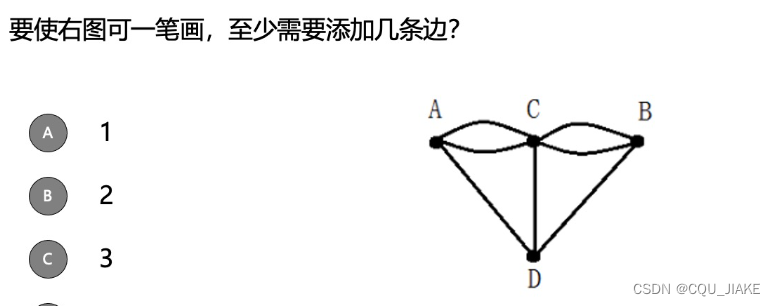

B是要回到出发点，即欧拉回路；A是一笔画即可

当前这个图4个结点度数都为奇数，添一条边使2个结点的奇数度数的结点为偶数，故添一条边会使奇数的点个数变为2，可构成欧拉路径

判断欧拉回路代码


int n, m, degree[1001];
int s, t;
while (cin >> n) {bool flag = 1;for (int i = 0; i < n; i++) {degree[i] = 0;}cin >> m;for (int i = 1; i <= m; i++) {cin >> a >> b;degree[a]++;degree[b]++;}for (int i = 0; i < n; i++) {if (degree[i] % 2 != 0) {flag = 0;break;}}cout << flag ? "YES" : "NO";
}

这段代码是一个用来判断无向图是否为欧拉图的程序。

主要流程如下：
- 声明了整型变量 `n` 和 `m`，以及一个整型数组 `degree` 用来记录每个顶点的度数。
- 使用循环不断读入顶点的数量 `n`，如果 `n` 不等于 0，则继续执行程序。（每个测试样例）
- 在每个循环中，首先读入边的数量 `m`。
- 设置一个标志变量 `flag` 初始化为 1。
- 使用 `memset` 函数将 `degree` 数组初始化为 0。
- 使用一个循环读入每条边，并更新对应顶点的度数。
- 再使用一个循环遍历每个顶点，如果某个顶点的度数为奇数，则将 `flag` 置为 0。
- 最后，输出 `flag` 的值，表示是否为欧拉图。

整个程序的目的是判断给定的无向图是否为欧拉图，其中欧拉图的定义是每个顶点的度数都为偶数。如果是欧拉图，则输出 1，否则输出 0。

这里是默认结点编号从0开始，如果从1开始则需要小小修改一下。

图有两个重要参数，一个是顶点，一个是边数

只有存在边时，才会使顶点的度发生改变

图的性质

图的存储

图有两个重要参数，一个是顶点，一个是边数

只有存在边时，才会使顶点的度发生改变

数组可以用来存储结点，也可以用来存储边

定义结构体也可以定义结点或边

邻接表

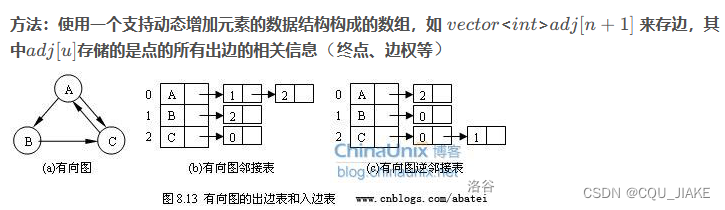
在有向图中，只有可以达到才会是邻居

struct node{vector<int> v;
}a[MAXN];for (int i = 1 ; i <= m ; i ++) {int u , v;scanf("%d %d", &u , &v);a[u].v.push_back(v);a[v].v.push_back(u);	
} 
return 0;

有m条边。这里是无向图的邻接表法

链式前向星

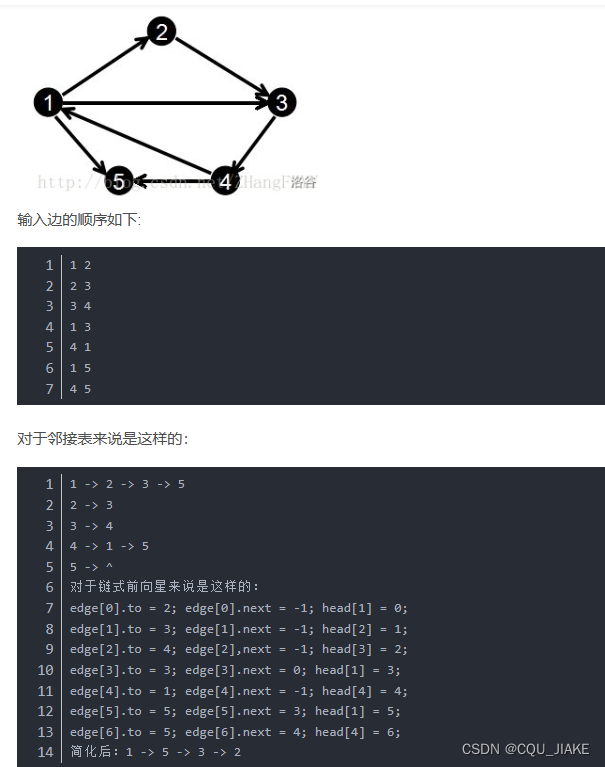
edge的数组下标编号代表边的编号，按照边的输入顺序依次存储。

head数组下标代表图的结点的编号，head[u]表示以u为起点的一条边

struct edge{int to , nxt , w;
};
edge a[MAXN];
void add(int u , int v , int w) {a[cnt].w = w;a[cnt].to = v;a[cnt].nxt = head[u];head[u] = cnt ++;
}

这段代码是用来实现添加边的函数。

- 定义了一个结构体 `edge`，其中包含三个整数变量 `to`、`nxt` 和 `w`，分别表示边的终点、下一条边的索引和边的权重。
- 声明了一个名为 `a` 的结构体数组，作为表示图的边集合，大小为 MAXN。
- 声明了一个静态整数变量 `cnt`，用于记录边的数量。
- 声明了一个名为 `head` 的整数数组，用于记录每个顶点的最近新插入边的索引。
- 定义了一个名为 `add` 的函数，用于添加一条从顶点 `u` 到顶点 `v` 的边，并设置边的权重为 `w`。
- 在 `add` 函数中，将当前边的权重、终点和下一条边的索引分别赋值给 `a[cnt].w`、`a[cnt].to` 和 `a[cnt].nxt`，然后将 `cnt` 的值赋给 `head[u]`，即将当前边的索引存储在顶点 `u` 的第一条边上。
- 最后，将 `cnt` 的值递增一次。

通过调用 `add` 函数，可以在图中添加一条从顶点 `u` 到顶点 `v` 的边，同时设置该边的权重为 `w`。

图的遍历

求连通分量

在遍历过程中通过vis数组，以及一个cnt计数可以确定连通分量

有向图DFS

void dfs(int k) {if (vis[k]) return;vis[k] = 1;printf("%d ", k);for (set<int>:: iterator it = st[k].begin() ; it != st[k].end() ; it ++) {dfs(*it);}
}
for (int i = 1 ; i <= m ; i ++) {int u , v;scanf("%d %d", &u , &v);st[u].insert(v);
} 
dfs(1);
for (int i = 1 ; i <= n ; i ++) {if (!vis[i]) dfs(i);
}

由于是有向图，在邻接表法中，只要写st[u].insert[v]

使用一个循环遍历顶点 k 对应的邻接集合 st[k]，对于每个相邻的顶点 v，递归调用 dfs 函数进行深度优先搜索。

在主函数中，使用一个循环读取 m 条边的信息，并将每条边的尾部顶点插入到起始顶点对应的邻接集合 st[u] 中。

接着，调用 dfs(1)，以顶点 1 为起点进行深度优先搜索。该步骤将遍历与顶点 1 相连的所有顶点。

最后，使用一个循环遍历所有顶点，如果某个顶点尚未被访问过，则调用 dfs 函数对该顶点进行深度优先搜索。这样可以确保遍历图中的所有连通分量。

通过vis数组可以确定图的连通分量

有向图BFS

void bfs(int k) {q.push(k);while(!q.empty()) {int x = q.front();q.pop();if (vis[x]) continue;vis[x] = 1;printf("%d ", x);for (set<int>:: iterator it = st[x].begin() ; it != st[x].end() ; it ++) {q.push(*it);}}
}
for (int i = 1 ; i <= m ; i ++) {int u , v;scanf("%d %d", &u , &v);st[u].insert(v);	
} 
bfs(1);
for (int i = 1 ; i <= n ; i ++) {if (!vis[i]) bfs(i);
}

无向图BFS

void bfs() {q.push(rt);while(!q.empty()) {int x = q.front();q.pop();if (vis[x]) continue;vis[x] = 1;printf("%d ", x);for (int i = 1 ; i <= n ; i ++) {if (adj[x][i]) {q.push(i);}}}
}
for (int i = 1 ; i <= m ; i ++) {int u , v;scanf("%d %d", &u , &v);adj[u][v] = 1;adj[v][u] = 1;	
}

无向图和有向图最主要区别是，采用数据结构不一样。有向图用集合，可以自动从小到大，无向图用矩阵，定一结点，遍历以该结点为起点的矩阵行