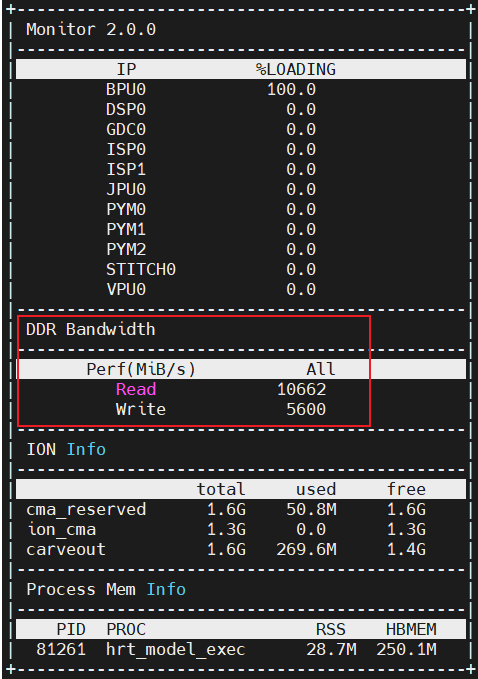
2025.1.14——1200

2025.1.14——1200

---

Q1. 1200

You have \(n\) sticks, numbered from \(1\) to \(n\). The length of the \(i\)-th stick is \(2^{a_i}\).

You want to choose exactly \(3\) sticks out of the given \(n\) sticks, and form a non-degenerate triangle out of them, using the sticks as the sides of the triangle. A triangle is called non-degenerate if its area is strictly greater than \(0\).

You have to calculate the number of ways to choose exactly \(3\) sticks so that a triangle can be formed out of them. Note that the order of choosing sticks does not matter (for example, choosing the \(1\)-st, \(2\)-nd and \(4\)-th stick is the same as choosing the \(2\)-nd, \(4\)-th and \(1\)-st stick).
Input

• the first line contains one integer \(n\) (\(1 \le n \le 3 \cdot 10^5\));
• the second line contains \(n\) integers \(a_1, a_2, \dots, a_n\) (\(0 \le a_i \le n\)).

---

Q2. 1200

Masha and Olya have an important team olympiad coming up soon. In honor of this, Masha, for warm-up, suggested playing a game with Olya:

There is an array \(a\) of size \(n\). Masha goes first, and the players take turns. Each move is described by the following sequence of actions:

\(\bullet\) If the size of the array is \(1\), the game ends.

\(\bullet\) The player who is currently playing chooses two different indices \(i\), \(j\) (\(1 \le i, j \le |a|\)), and performs the following operation — removes \(a_i\) and \(a_j\) from the array and adds to the array a number equal to \(\lfloor \frac{a_i + a_j}{2} \rfloor \cdot 2\). In other words, first divides the sum of the numbers \(a_i\), \(a_j\) by \(2\) rounding down, and then multiplies the result by \(2\).

Masha aims to maximize the final number, while Olya aims to minimize it.

Masha and Olya decided to play on each non-empty prefix of the initial array \(a\), and asked for your help.

For each \(k = 1, 2, \ldots, n\), answer the following question. Let only the first \(k\) elements of the array \(a\) be present in the game, with indices \(1, 2, \ldots, k\) respectively. What number will remain at the end with optimal play by both players?
Input

The first line of each test case contains a single integer \(n\) (\(1 \le n \le 10^5\)) — the size of the array.

The second line contains \(n\) integers \(a_1,a_2, \ldots,a_n\) (\(1 \leq a_i \leq 10^9\)) — the array on which Masha and Olya play.

---

Q3. 1200

Vlad found a string \(s\) consisting of \(n\) lowercase Latin letters, and he wants to make it as short as possible.

To do this, he can remove any pair of adjacent characters from \(s\) any number of times, provided they are different. For example, if \(s\)=racoon, then by removing one pair of characters he can obtain the strings coon, roon, raon, and raco, but he cannot obtain racn (because the removed letters were the same) or rcon (because the removed letters were not adjacent).

What is the minimum length Vlad can achieve by applying any number of deletions?
Input

The first line of each test case contains a single integer \(n\) (\(1 \le n \le 2 \cdot 10^5\)) — the length of the string \(s\).

The second line of each test case contains the string \(s\) consisting of \(n\) lowercase Latin letters.

---

Q4. 1200

Monocarp tries to get home from work. He is currently at the point \(O = (0, 0)\) of a two-dimensional plane; his house is at the point \(P = (P_x, P_y)\).

Unfortunately, it is late in the evening, so it is very dark. Monocarp is afraid of the darkness. He would like to go home along a path illuminated by something.

Thankfully, there are two lanterns, located in the points \(A = (A_x, A_y)\) and \(B = (B_x, B_y)\). You can choose any non-negative number \(w\) and set the power of both lanterns to \(w\). If a lantern's power is set to \(w\), it illuminates a circle of radius \(w\) centered at the lantern location (including the borders of the circle).

You have to choose the minimum non-negative value \(w\) for the power of the lanterns in such a way that there is a path from the point \(O\) to the point \(P\) which is completely illuminated. You may assume that the lanterns don't interfere with Monocarp's movement.

The picture for the first two test cases

---

------------------------独自思考分割线------------------------

• 结论+博弈+结论+结论

---

A1.

1. 发现贡献可以缩小选择范围：只有等腰或等边三角形。
2. 组合一下计算方案数。

---

A2.

1. 本质就是发现损失的原因和决策。
2. 根据奇偶性博弈一下发现损失和奇数的个数有一定关系。

---

A3.

1. 思考最后答案的形态是同一个字母。
2. 充分性策略：考虑最多的那个字母，尽量去消去它，而且在其他字母存在的时候一定可以消去它。
3. 未消完剩下的就是最优答案，消完再讨论下奇偶决定答案0/1。

---

A4.

1. 必要性：\(O\) 点与 \(P\) 点一定需要被照亮。
2. 充分性：两点被同一灯照亮/两灯都有参与并且两灯有连接。
3. 数学一下：两种情况两灯互换一下 四种结果取最小值。

---

------------------------代码分割线------------------------

A1.

#include <bits/stdc++.h>
#define int long long //
#define endl '\n'     // 交互/调试 关
using namespace std;
#define bug(BUG) cout << "bug:# " << (BUG) << endl
#define bug2(BUG1, BUG2) cout << "bug:# " << (BUG1) << " " << (BUG2) << endl
#define bug3(BUG1, BUG2, BUG3) cout << "bug:# " << (BUG1) << ' ' << (BUG2) << ' ' << (BUG3) << endl
void _();
signed main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cout << fixed << setprecision(6);int T = 1;cin >> T;while (T--)_();return 0;
}void _()
{int n;cin >> n;map<int, int> cnt;for (int i = 1; i <= n; i++){int x;cin >> x;cnt[x]++;}int res = 0;auto cal = [](int n){return n * (n - 1) * (n - 2) / 6;};int has = 0;for (auto [x, k] : cnt){if (k >= 2)res += has * k * (k - 1) / 2;if (k >= 3)res += cal(k);has += k;}cout << res << endl;
}

---

A2.

#include <bits/stdc++.h>
#define int long long //
#define endl '\n'     // 交互/调试 关
using namespace std;
#define bug(BUG) cout << "bug:# " << (BUG) << endl
#define bug2(BUG1, BUG2) cout << "bug:# " << (BUG1) << " " << (BUG2) << endl
#define bug3(BUG1, BUG2, BUG3) cout << "bug:# " << (BUG1) << ' ' << (BUG2) << ' ' << (BUG3) << endl
void _();
signed main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cout << fixed << setprecision(6);int T = 1;cin >> T;while (T--)_();return 0;
}void _()
{int n;cin >> n;int sum = 0;int odd = 0;for (int i = 0; i < n; i++){int x;cin >> x;sum += x;odd += x & 1 != 0;int k = 0;if (i){k = (odd + 2) / 3;if (odd % 3 == 2)k--;}cout << sum - k << ' ';}cout << endl;
}

---

A3.

#include <bits/stdc++.h>
#define int long long //
#define endl '\n'     // 交互/调试 关
using namespace std;
#define bug(BUG) cout << "bug:# " << (BUG) << endl
#define bug2(BUG1, BUG2) cout << "bug:# " << (BUG1) << " " << (BUG2) << endl
#define bug3(BUG1, BUG2, BUG3) cout << "bug:# " << (BUG1) << ' ' << (BUG2) << ' ' << (BUG3) << endl
void _();
signed main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cout << fixed << setprecision(6);int T = 1;cin >> T;while (T--)_();return 0;
}void _()
{int n;cin >> n;map<char, int> cnt;int max_cnt = 0;string s;cin >> s;for (auto v : s){cnt[v]++;max_cnt = max(max_cnt, cnt[v]);}int res = max(0ll, max_cnt - (n - max_cnt));if (n & 1)res = max(1ll, res);cout << res << endl;
}

---

A4.

#include <bits/stdc++.h>
#define int long long //
#define endl '\n'     // 交互/调试 关
using namespace std;
#define bug(BUG) cout << "bug:# " << (BUG) << endl
#define bug2(BUG1, BUG2) cout << "bug:# " << (BUG1) << " " << (BUG2) << endl
#define bug3(BUG1, BUG2, BUG3) cout << "bug:# " << (BUG1) << ' ' << (BUG2) << ' ' << (BUG3) << endl
void _();
signed main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cout << fixed << setprecision(10);int T = 1;cin >> T;while (T--)_();return 0;
}#define x first
#define y second
void _()
{pair<int, int> o, p, a, b;o.x = o.y = 0;cin >> p.x >> p.y >> a.x >> a.y >> b.x >> b.y;auto d = [](pair<int, int> a, pair<int, int> b){return sqrt(1.0 * (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));};double res = min(max(d(a, o), d(a, p)), max(d(b, o), d(b, p)));res = min(res, max(d(a, b) / 2, min(max(d(a, o), d(b, p)), max(d(b, o), d(a, p)))));cout << res << endl;
}

---