朴素贝叶斯（Naive Bayes ,NB）算法是基于贝叶斯定理与特征条件独立假设的分类方法，该算法是有监督的学习算法，解决的是分类问题，是将一个未知样本分到几个预先已知类别的过程。

朴素贝叶斯的思想就是根据某些个先验概率计算Y变量属于某个类别的后验概率，也就是根据先前事件的有关数据估计未来某个事件发生的概率。

1、举例：

一个学校内有60%的学生是男生，40%的学生是女生。根据统计，男生总是穿长裤，女生则有一半穿长裤，一半穿裙子。

问题：

假设在校园中随机抽取一个穿长裤的学生，推断该学生是女生的概率？

已知：

P(男生) = 60%

P(女生) = 40%

P(长裤|女生) = 50%

P(裙子|女生) = 50%

求： P(女生|长裤)—穿长裤人数中是女生的概率？

要知道穿长裤的人是女生的概率，要知道穿长裤女生的人数，也要知道穿长裤的总人数，两者相除就是长裤中女生的概率。假设学校人数为U

穿长裤总人数 = 穿长裤的男生人数+穿长裤的女生人数

= 60% * U + 40% * U *50%

穿长裤女生的人数 = 40% * U * 50%

随机抽取一个穿长裤的学生是女生的概率  

=  穿长裤女生的人数/穿长裤总人数

=  40% * U * 50% /  ( 60% * U + 40% * U *50%)

  =  0.25

假设学生穿长裤记作事件A，学生穿长裤的概率就是P(A)。学生是女生记作事件B，学生是女生的概率是P(B)，求:抽取的这个穿长裤学生是女生的概率（P(B|A)）？

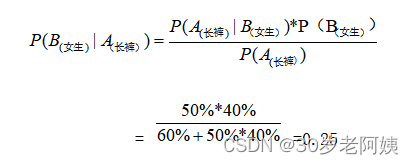
2、朴素贝叶斯公式

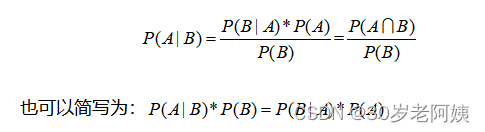
其中:

P(A)叫做A事件的先验概率，即一般情况下，认为A发生的概率。

P(B|A)叫做似然度，是A假设条件成立的情况下发生B的概率。

P(A|B)叫做后验概率，在B发生的情况下发生A的概率，也就是要求的概率。P(B)叫做标准化常量，即在一般情况下，认为B发生的概率。

3、理解朴素贝叶斯

假设现在有一堆邮件，正常邮件的比例是80%，垃圾邮件的比例是20%，这堆邮件中，5%的邮件中出现Viagra单词，如果有一封邮件，这封邮件中包含Viagra单词，求这封邮件是垃圾邮件的概率。

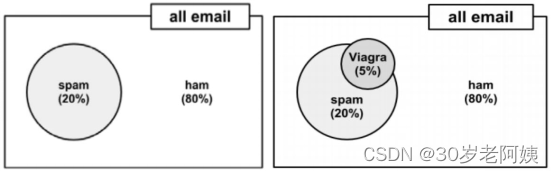
显然不能使用5%*20%=1%得到这封邮件是垃圾邮件的概率，因为垃圾邮件中有可能出现Viagra也有可能不会出现Viagra单词。那么根据贝叶斯公式可得包含Viagra单词的邮件是垃圾邮件的概率为：

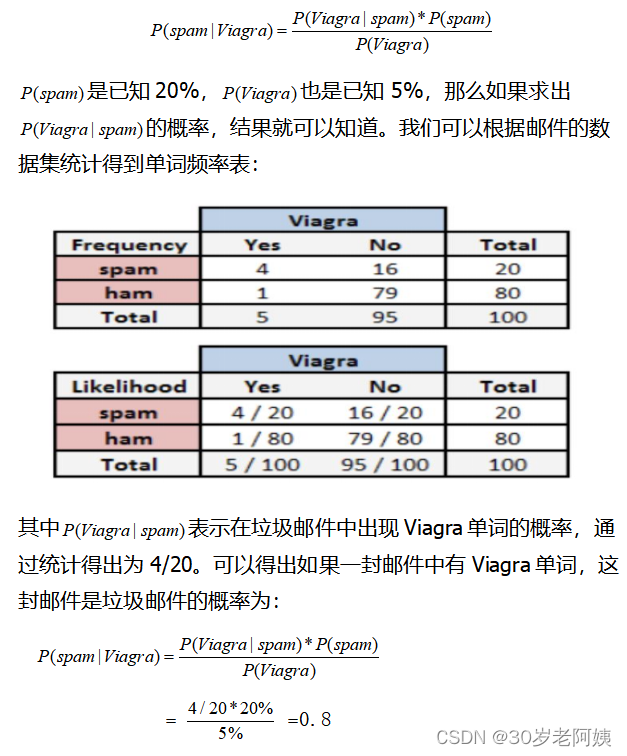
通过同样的计算可以得到，含有Viagra单词但不是垃圾邮件的概率为0.2。那么可以认为这封邮件是垃圾邮件的概率比较大。这里的Viagra可以理解为邮件中的一个特征。那么当一封邮件有额外更多的特征时，贝叶斯如何扩展？

假设所有历史邮件中只出现了4个单词，也就是4个特征，根据历史邮件统计的单词频率表如下：

假设现在给定一封邮件中有Viagra和Unsubscribe(取消订阅)两个单词，求这封邮件是垃圾邮件的概率、不是垃圾邮件的概率？

利用贝叶斯公式，我们可以得到： 

是垃圾邮件的概率：

4、拉普拉斯估计

根据以上例子，假设有一封邮件这4个单词都出现了，求这封邮件是垃圾邮件的概率：

拉普拉斯估计本质上是给频率表中的每个单词的计数加上一个较小的数，这样就保证每一类中每个特征发生的概率非零。通常，拉普拉斯估计中加上的数值为1，这样就保证了每一个特征至少在数据中出现一次。

以上例子如果四个单词都出现情况下计算是否是垃圾邮件，出现

的概率为0/20，可以增加4封垃圾邮件，使4封邮件中每个邮件中只有一个单词出现，这样就避免了垃圾邮件中有的单词出现概率为0的情况。同样在不是垃圾邮件中也增加4封，避免在正常邮件中出现有的单词出现概率为0的情况。