import torch
import numpy as np
import torch.nn as nn
import matplotlib.pyplot as plt

生成测试数据

# 长期趋势
def trend(time, slope=0):return slope * time# 季节趋势
def seasonal_pattern(season_time):return np.where(season_time < 0.4,np.cos(season_time * 2 * np.pi),1 / np.exp(3 * season_time))
def seasonality(time, period, amplitude=1, phase=0):season_time = ((time + phase) % period) / periodreturn amplitude * seasonal_pattern(season_time)# 噪声
def noise(time, noise_level=1):return np.random.randn(len(time)) * noise_level

X = torch.arange(1, 1001)
# Y = 0.7 * X + 100 + torch.randn(X.size())
Y = trend(X, 0.3) + seasonality(X, period=365, amplitude=30) + noise(X, 15) + 200
X.shape, Y.shape

(torch.Size([1000]), torch.Size([1000]))

plt.plot(X.numpy(), Y.numpy());

对测试数据进行处理

# 模型的数据的类型需要是32位浮点型
X = X.type(torch.float32)
Y = Y.type(torch.float32)
X.dtype, Y.dtype

(torch.float32, torch.float32)

# 模型的数据需要进行归一化或者标准化，下面是归一化
X = (X - X.min()) / (X.max() - X.min())
Y = (Y - Y.min()) / (Y.max() - Y.min())
plt.plot(X.numpy(), Y.numpy());

定义模型和模型参数

# 线性模型只有两个参数斜率k，和偏置b
# 线性模型的方程为y = k * x + b
k = nn.Parameter(torch.rand(1, dtype=torch.float32))
b = nn.Parameter(torch.rand(1, dtype=torch.float32))
# 下面输出中的requires_grad=True 表示该参数需要计算梯度
# 梯度用于在反向传播中对参数进行优化，优化方法即梯度下降
k, b 

(Parameter containing:tensor([0.6231], requires_grad=True),Parameter containing:tensor([0.0044], requires_grad=True))

def linear_model(x):return k * x + b

梯度下降优化参数

# 可以通过改变学习率lr和epoch_num学习各自的用途

# 定义优化器，用于更新模型的参数，即传入的k和b
optimizer = torch.optim.SGD([k, b], lr=0.01)
# 损失函数，模型优化的目的
loss_func = nn.MSELoss()# 每个epoch表示把全部的数据过一遍
epoch_num = 2000
for epoch in range(epoch_num):# 获取模型预测结果y_pred = linear_model(X)# 计算损失值loss = loss_func(y_pred, Y)# 将梯度设为0optimizer.zero_grad()# 反向传播，计算梯度loss.backward()# 执行梯度下降，优化参数optimizer.step()
k, b

(Parameter containing:tensor([0.8825], requires_grad=True),Parameter containing:tensor([0.0419], requires_grad=True))

# detach()函数用于将参数设置为不需要梯度
k2 = k.detach().numpy()[0]
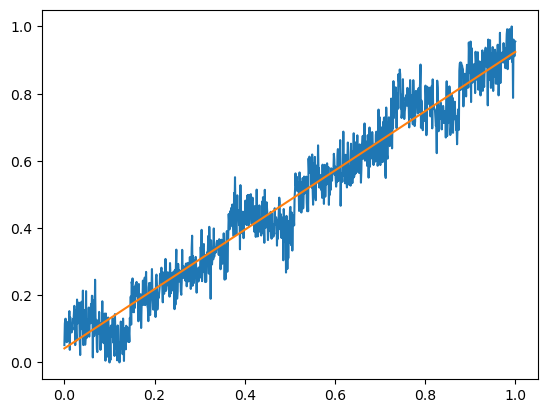
b2 = b.detach().numpy()[0]plt.plot(X, Y);
plt.plot(X, k2 * X + b2);

优化模型

class LinearModel(nn.Module):def __init__(self):super().__init__()self.k = nn.Parameter(torch.rand(1, dtype=torch.float32))self.b = nn.Parameter(torch.rand(1, dtype=torch.float32))def forward(self, x):return self.k * x + self.b

model = LinearModel()
# 定义优化器，用于更新模型的参数，即传入的k和b
optimizer = torch.optim.SGD([k, b], lr=0.01)
# 损失函数，模型优化的目的
loss_func = nn.MSELoss()epoch_num = 2000
for epoch in range(epoch_num):y_pred = model(X)loss = loss_func(y_pred, Y)optimizer.zero_grad()loss.backward()optimizer.step()
k, b

(Parameter containing:tensor([0.8825], requires_grad=True),Parameter containing:tensor([0.0419], requires_grad=True))

k2 = k.detach().numpy()[0]
b2 = b.detach().numpy()[0]plt.plot(X, Y);
plt.plot(X, k2 * X + b2);

随机梯度下降

# 前面执行梯度下降时，我们是一次将全部的数据都传入模型
# 但在实际应用中，可能会由于数据太大，没法全部传入模型
# 因此，可以一次传入一部分数据，这便是随机梯度下降
# 随机梯度下降的核心是，梯度是期望。期望可使用小规模的样本近似估计。

model = LinearModel()
# 定义优化器，用于更新模型的参数，即传入的k和b
optimizer = torch.optim.SGD([k, b], lr=0.01)
# 损失函数，模型优化的目的
loss_func = nn.MSELoss()# 每个epoch表示把全部的数据过一遍
epoch_num = 2000 
# iter_step表示在一个epoch内抽取几个小规模样本
iter_step = 10
# batch_size表示小规模样本的大小
batch_size = 100
for epoch in range(epoch_num):for i in range(iter_step):random_samples = torch.randint(X.size()[0], (batch_size, ))X_i, Y_i = X[random_samples], Y[random_samples]y_pred = model(X_i)loss = loss_func(y_pred, Y_i)optimizer.zero_grad()loss.backward()optimizer.step()
k, b

(Parameter containing:tensor([0.8825], requires_grad=True),Parameter containing:tensor([0.0419], requires_grad=True))

k2 = k.detach().numpy()[0]
b2 = b.detach().numpy()[0]plt.plot(X, Y);
plt.plot(X, k2 * X + b2);