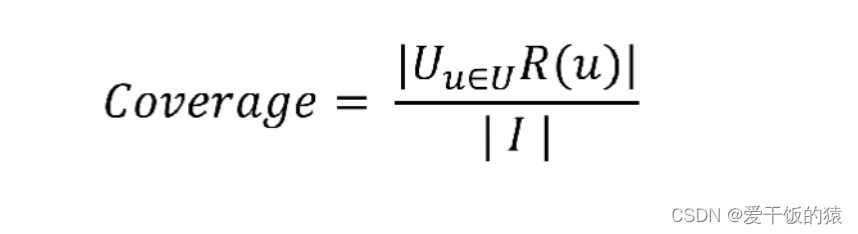【深度学习】一维数组的聚类-编程知识

在学习聚类算法的过程中，学习到的聚类算法大部分都是针对n维的，针对一维数据的聚类方式较少，今天就来学习下如何给一维的数据进行聚类。

方案一：采用K-Means对一维数据聚类

Python代码如下：

  from sklearn.cluster import KMeans
import numpy as np
x = np.random.random(10000)
y = x.reshape(-1,1)
km = KMeans()
km.fit(y)

核心的操作是y = x.reshape(-1,1)，含义为将一维数据变成只有1列，行数不知道多少（-1代表根据剩下的维度计算出数组的另外一个shape属性值）。

方案二：采用一维聚类方法Jenks Natural Breaks

Jenks Natural Breaks（自然断点分类）。一般来说，分类的原则就是差不多的放在一起，分成若干类。统计上可以用方差来衡量，通过计算每类的方差，再计算这些方差之和，用方差和的大小来比较分类的好坏。因而需要计算各种分类的方差和，其值最小的就是最优的分类结果（但并不唯一）。这也是自然断点分类法的原理。另外，当你去看数据的分布时，可以比较明显的发现断裂之处，这些断裂之处和Jenks Natural Breaks方法算出来也是一致的。因而这种分类法很“自然”。

Jenks Natural Breaks和K Means在一维数据时，完全等价。它们的目标函数一样，但是算法的步骤不完全相同。K Means是先设定好K个初始随机点。而Jenks Breaks则是用遍历的方法，一个点一个点地移动，直到达到最小值。

Natural Breaks算法又有两种：

Jenks-Caspall algorithm(1971)，是Jenks和Caspall发明的算法。原理就如前所述，实现的时候要将每种分类情况都计算一遍，找到方差和最小的那一种，计算量极大。n个数分成k类，就要从n-1个数中找k-1个组合，这个数目是很惊人的。数据量较大时，如果分类又多，以当时的计算机水平根本不能穷举各种可能性。
Fisher-Jenks algorithm(1977)，Fisher(1958)发明了一种算法提高计算效率，不需要进行穷举。Jenks将这种方法引入到数据分类中。但后来者几乎只知道Jenks而不知Fisher了。

具体算法实现：

Jenks-Caspall algorithm：https://github.com/domlysz/Jenks-Caspall.py
Fisher-Jenks algorithm：https://github.com/mthh/jenkspy

和K-Means一样，使用Jenks Natural Breaks需要先确定聚类数量K值。常见的方法是：GVF（The Goodness of Variance Fit）。GVF，翻译过来是“方差拟合优度”，公式如下：

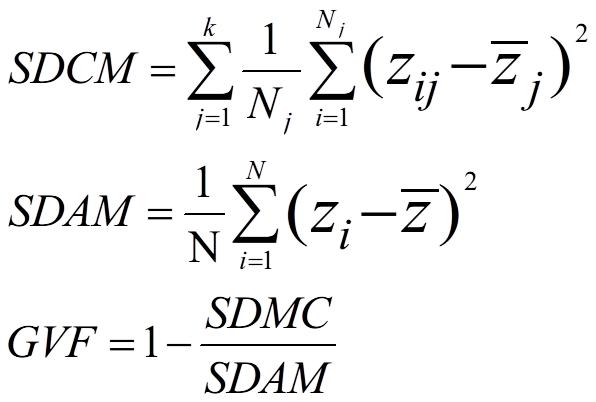
一维数组的聚类-图片1

其中，SDAM是the Sum of squared Deviations from the Array Mean，即原始数据的方差；SDCM是the Sum of squared Deviations about Class Mean，即每一类方差的和。显然，SDAM是一个常数，而SDCM与分类数k有关。一定范围内，GVF越大，分类效果越好。SDCM越小，GVF越大，越接近于1。而SDCM随k的增大而大，当k等于n时，SDMC=0，GVF=1。

GVF用于判定不同分类数的分类效果好坏。以k和GVF做图可得：

一维数组的聚类-图片2

随着k的增大，GVF曲线变得越来越平缓。特别是在红线处（k=5），曲线变得基本平坦（之前起伏较大，之后起伏较小），k(5)也不是很大，所以可以分为5类。一般来说，GVF>0.7就可以接受了，当然越高越好，但一定要考虑k不能太大。显然，这是一个经验公式，但总比没有好吧。

代码示例：

  from jenkspy import jenks_breaks
import numpy as np
 
 
def goodness_of_variance_fit(array, classes):
    # get the break points
    classes = jenks_breaks(array, classes)
 
    # do the actual classification
    classified = np.array([classify(i, classes) for i in array])
 
    # max value of zones
    maxz = max(classified)
 
    # nested list of zone indices
    zone_indices = [[idx for idx, val in enumerate(classified) if zone + 1  val] for zone in range(maxz)]
 
    # sum of squared deviations from array mean
    sdam = np.sum((array - array.mean())  2)
 
    # sorted polygon stats
    array_sort = [np.array([array[index] for index in zone]) for zone in zone_indices]
 
    # sum of squared deviations of class means
    sdcm = sum([np.sum((classified - classified.mean())  2) for classified in array_sort])
 
    # goodness of variance fit
    gvf = (sdam - sdcm) / sdam
 
    return gvf
 
 
def classify(value, breaks):
    for i in range(1, len(breaks)):
        if value < breaks[i]:
            return i
    return len(breaks) - 1
 
 
if name  ‘main’:
    gvf = 0.0
    nclasses = 2
    array = np.random.random(10000)
    while gvf < .8:
        gvf = goodness_of_variance_fit(array, nclasses)
        print(nclasses, gvf)
        nclasses += 1

参考链接：

https://en.wikipedia.org/wiki/Jenks_natural_breaks_optimization
https://macwright.org/2013/02/18/literate-jenks.html

方案三：核密度估计Kernel Density Estimation

所谓核密度估计，就是采用平滑的峰值函数(“核”)来拟合观察到的数据点，从而对真实的概率分布曲线进行模拟。核密度估计更多详细内容，可以参考先前的Mean Shift聚类中的相关说明。

使用示例：

  import numpy as np
from scipy.signal import argrelextrema
import matplotlib.pyplot as plt
from sklearn.neighbors.kde import KernelDensity
 
a = np.array([10, 11, 9, 23, 21, 11, 45, 20, 11, 12]).reshape(-1, 1)
kde = KernelDensity(kernel=‘gaussian’, bandwidth=3).fit(a)
s = np.linspace(0, 50)
e = kde.score_samples(s.reshape(-1, 1))
plt.plot(s, e)
plt.show()
 
mi, ma = argrelextrema(e, np.less)[0], argrelextrema(e, np.greater)[0]
print(“Minima:”, s[mi])
print(“Maxima:”, s[ma])
print(a[a < mi[0]], a[(a >= mi[0]) * (a <= mi[1])], a[a >= mi[1]])
 
plt.plot(s[:mi[0] + 1], e[:mi[0] + 1], ‘r’,
         s[mi[0]:mi[1] + 1], e[mi[0]:mi[1] + 1], ‘g’,
         s[mi[1]:], e[mi[1]:], ‘b’,
         s[ma], e[ma], ‘go’,
         s[mi], e[mi], ‘ro’)
plt.show()

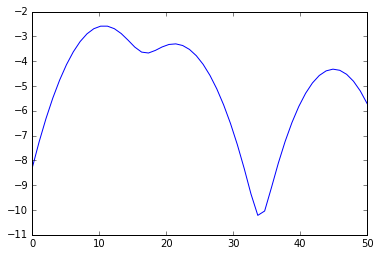
输出内容：

  Minima: [17.34693878 33.67346939]
Maxima: [10.20408163 21.42857143 44.89795918]
[10 11  9 11 11 12] [23 21 20] [45]

一维数组的聚类-图片3

一维数组的聚类-图片4

参考链接：

https://en.wikipedia.org/wiki/Kernel_density_estimation
http://scikit-learn.org/stable/auto_examples/neighbors/plot_kde_1d.html
https://jakevdp.github.io/blog/2013/12/01/kernel-density-estimation/