3.6 numpy库
目录
1. 数据的维度
2. numpy基础知识
3. ndarray数组的创建
4. ndarray数组的操作
5. numpy广播机制
6. numpy的运算及函数库
7.numpy文件存取
1. 数据的维度
一个数据表达一个含义,而一组数据表达一个或多个含义。
维度:是一组数据的组织形式
一维数据:由对等关系的有序或无序数据构成,采用线性方式组织,对应列表、数组和集合等概念。
列表:数据类型可以不同
数组:数据类型相同
二维数据:由多个一维数据构成,是一维数据的组合形式。
表格是典型的二维数据,其中,表头是二维数据的一部分
多维数据:由一维或二维数据在新维度上扩展形成。
数据维度的Python表示:
- 一维数据:列表和集合类型
- 二维数据:列表类型
- 多维数据:列表类型
- 高维数据:字典类型或其它如JSON、XML和YAML格式
2. numpy基础知识
2.1 numpy概述
numpy是开源的Python科学计算基础库,包含:
- 强大的N维数组对象ndarray(Array; Matrix)
- 成熟的(广播)函数库
- 整合了C/C++/Fortran代码的工具
- 实用的线性代数、傅里叶变换和随机数生成函数
- 与稀疏矩阵运算包scipy配合使用更加方便
numpy是SciPy、Pandas等数据处理或科学计算库的基础。它提供了许多高级的数值编程工具,如:矩阵数据类型、矢量处理,以及精密的运算库,为进行严格的数字处理而产生。很多大型金融公司,以及核心的科学计算组织如:Lawrence Livermore,NASA都在用其处理一些本来使用C++,Fortran或Matlab等所做的任务。
2.2 numpy库的引用
Anaconda里面已经安装过numpy。
原生Python安装:
在控制台中输入:
pip install numpy
安装之后可以导入
import numpy as np
#尽管别名可以省略或更改,但建议使用以上约定俗成的别名“np“
3. ndarray数组的创建
3.1 N维数组对象ndarray
Python已有列表类型,为什么需要一个数组对象(类型)?
标准Python中用list(列表)保存值,可以当做数组使用,但因为列表中的元素可以是任何对象,所以浪费了CPU运算时间和内存。
numpy诞生为了弥补这些缺陷。它提供了两种基本的对象:
- ndarray:全称(n-dimensional array object)是储存单一数据类型的多维数组。
- ufunc:全称(universal function object)它是一种能够对数组进行处理的函数。
numpy中文官网
A和B是一维数组,计算A2+B3,示例如下:
# python基础语法方式
def pySum():a=[0,1,2,3,4]b=[5,6,7,8,9]c=[]for i in range(len(a)):c.append(a[i]+b[i])return c
print(pySum())
输出结果:
[5, 7, 9, 11, 13]
# numpy库方式
def npSum():a=np.array([0,1,2,3,4])b=np.array([5,6,7,8,9])return a+b
print(npSum())
输出结果:
[ 5 7 9 11 13]
N维数组对象:ndarray
ndarray是一个多维数组对象,由两部分构成:
- 实际的数据
- 描述这些数据的元数据(数据维度、数据类型等)
numpy 最重要的一个特点是其 N 维数组对象 ndarray,它是一系列同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
ndarray 对象是用于存放同类型(同质)元素的多维数组。
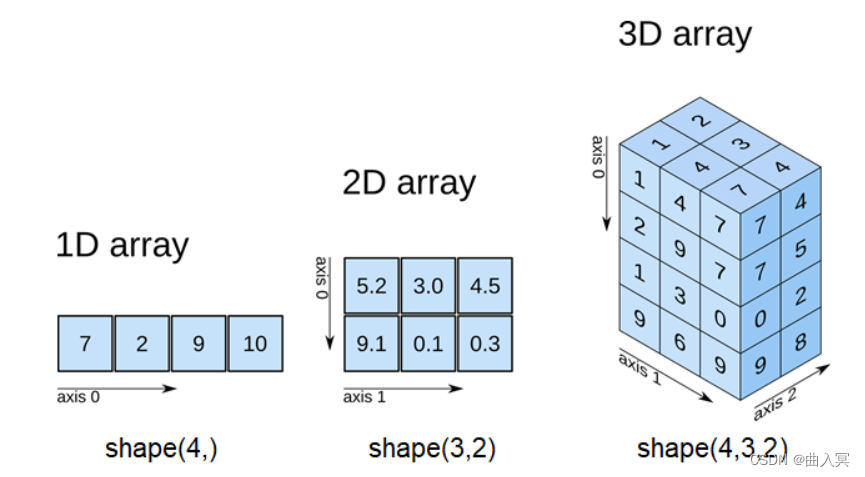
ndarray对维数没有限制。
小括号从左到右分别为第0轴,第1轴,第2轴,第3轴。
3.2 创建ndarray数组
ndarray数组的创建方法:
- 使用Python列表、元组创建ndarray数组
- 使用numpy函数创建ndarray数组
3.2.1 使用Python列表、元组创建ndarray数组
x = np.array(list/tuple)
x = np.array(list/tuple, dtype=np.float32)
当np.array()不指定dtype时,numpy将根据数据情况关联一个dtype类型
一维ndarray
import numpy as np
# 一维array
a = np.array([2,23,4], dtype=np.int32) # np.int默认为int32
print(a)
print(a.dtype)
输出结果:
[ 2 23 4]
int32
多维ndarray
# 多维array
a = np.array([[2,3,4],[3,4,5]])
print(a) # 生成2行3列的矩阵
输出结果:
[[2 3 4][3 4 5]]
c = np.array([(1,2,3),[4,5,6],(7,8,9)],dtype=np.float32)
c,c.dtype
输出结果:
(array([[1., 2., 3.],[4., 5., 6.],[7., 8., 9.]], dtype=float32),dtype('float32'))
3.2.2 使用numpy函数创建ndarray数组
| 函数 | 说明 |
|---|---|
| np.arange(n) | 类似range()函数,返回ndarray类型,元素从0到n‐1 |
| np.ones(shape) | 根据shape生成一个全1数组,shape是元组类型 |
| np.zeros(shape) | 根据shape生成一个全0数组,shape是元组类型 |
| np.full(shape,val) | 根据shape生成一个数组,每个元素值都是val |
| np.linspace() | 根据起止数据等间距地填充数据,形成数组 |
| np.empty(shape)) | 创建全空数组每个值都是接近于零的数 |
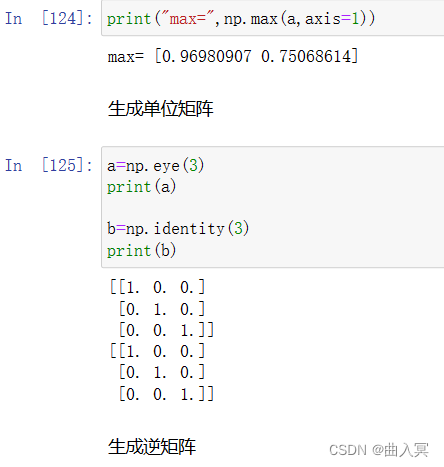
| np.eye(n) | 创建一个正方的n*n单位矩阵,对角线为1,其余为0 |
| np.ones_like(a) | 根据数组a的形状生成一个全1数组 |
| np.zeros_like(a) | 根据数组a的形状生成一个全0数组 |
| np.full_like(a,val) | 根据数组a的形状生成一个数组,每个元素值都是val |
| np.concatenate() | 将两个或多个数组合并成一个新的数组 |
创建连续数组
# 创建连续数组
a = np.arange(10,41,2) # 10-20的数据,步长为2
print(a)
#输出结果:[10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40]
创建全1数据
# 创建全一数据,同时指定数据类型
a = np.ones((3,4),dtype=np.int32)
print(a)
# 创建全一数据,同时指定数据类型
a = np.ones((3,4),dtype=np.int32)
print(a)#输出结果:
[[1 1 1 1][1 1 1 1][1 1 1 1]]
创建全零数组
a = np.zeros((3,4))
print(a) # 生成3行4列的全零矩阵#输出结果:
[[0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.]]
创建全特定数值ndarray数组
a=np.full((3,4,5),10)
a.shape,a
输出结果:
((3, 4, 5),array([[[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10]],[[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10]],[[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10],[10, 10, 10, 10, 10]]]))
根据起止数据创建等间距序列数据
# 创建线段型数据
a = np.linspace(1,10,20) # 开始端1,结束端10,且分割成20个数据,生成线段
print(a)
输出结果:
[ 1. 1.47368421 1.94736842 2.42105263 2.89473684 3.368421053.84210526 4.31578947 4.78947368 5.26315789 5.73684211 6.210526326.68421053 7.15789474 7.63157895 8.10526316 8.57894737 9.052631589.52631579 10. ]
创建全空数组

3.3 ndarray数组的属性
| 属性 | 说明 |
|---|---|
| .ndim | 秩,即轴的数量或维度的数量 |
| .shape | ndarray数组的尺度,对于矩阵,n行m列 |
| .size | ndarray数组元素的个数,相当于.shape中n*m的值 |
| .dtype | ndarray数组的元素类型 |
| .itemsize | ndarray数组中每个元素的大小,以字节为单位 |
秩、维度、轴的数量
a=np.full((3,4,5),1.,dtype=np.float32)
print(a)
print('number of dim:', a.ndim)
输出结果:
[[[1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.]][[1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.]][[1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.][1. 1. 1. 1. 1.]]]
number of dim: 3

3.4 ndarray数组的元素类型
| 数据类型 | 说明 |
|---|---|
| bool | 布尔类型,True或False |
| intc | 与C语言中的int类型一致,一般是int32或int64 |
| intp | 用于索引的整数,与C语言中size_t一致,int32或int64 |
| int8 | 字节长度的整数,取值:[‐128,127] |
| int16 | 16位长度的整数,取值:[‐32768,32767] |
| int32 | 32位长度的整数,取值:[‐231,231‐1] |
| int64 | 64位长度的整数,取值:[‐263,263‐1] |
| uint8 | 8位无符号整数,取值:[0,255] |
| uint16 | 16位无符号整数,取值:[0,65535] |
| uint32 | 32位无符号整数,取值:[0,232‐1] |
| uint64 | 32位无符号整数,取值:[0,264‐1] |
| float16 | 16位半精度浮点数:1位符号位,5位指数,10位尾数 |
| float32 | 32位半精度浮点数:1位符号位,8位指数,23位尾数 |
| float64 | 64位半精度浮点数:1位符号位,11位指数,52位尾数 |
| complex64 | 复数类型,实部和虚部都是32位浮点数 |
| complex128 | 复数类型,实部和虚部都是64位浮点数 |
Python语法仅支持整数、浮点数和复数3种类型,而ndarray为什么要支持这么多种元素类型?
- 科学计算涉及数据较多,对存储和性能都有较高要求
- 对元素类型精细定义,有助于numpy合理使用存储空间并优化性能
- 对元素类型精细定义,有助于程序员对程序规模有合理评估
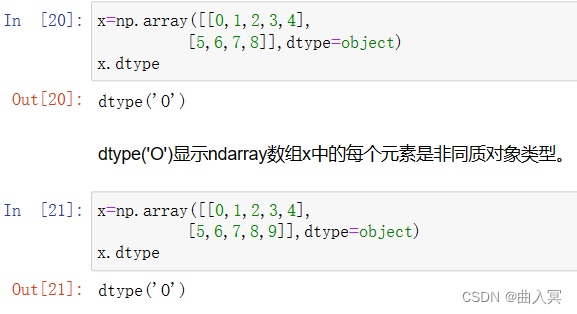
ndarray数组可以由非同质对象构成,非同质ndarray元素为对象类型,非同质ndarray数组无法有效发挥numpy优势,尽量避免使用。
3.5 ndarray数组的变换
对于创建后的ndarray数组,可以对其进行维度变换和元素类型变换。
| 方法 | 说明 |
|---|---|
| .reshape(shape) | 不改变数组元素,返回一个shape形状的数组,原数组不变 |
| .resize(shape) | 与.reshape()功能一致,但修改原数组 |
| .swapaxes(ax1,ax2) | 将数组n个维度中两个维度进行调换 |
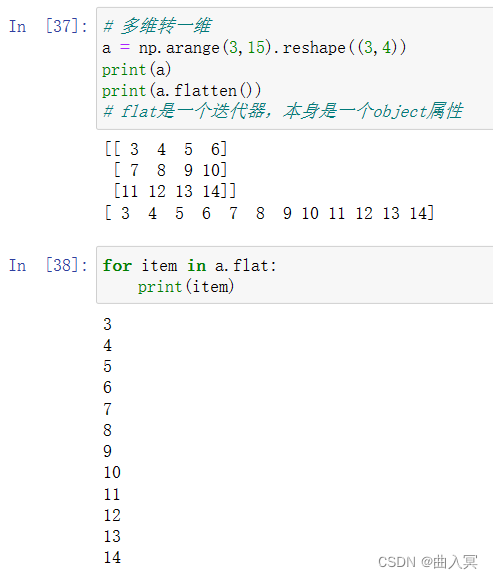
| .flatten() | 对数组进行降维,返回折叠后的一维数组,原数组不变 |
| .astype() | 对数组进行类型变换 |
| .tolist() | 将数据类型转换为列表 |
reshape操作
a = [ i for i in range(24)]
a=np.array(a)
print(a)
# 使用reshape改变上述数据的形状
b = a.reshape((4,6))
print(b)
输出结果:
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]
[[ 0 1 2 3 4 5][ 6 7 8 9 10 11][12 13 14 15 16 17][18 19 20 21 22 23]]
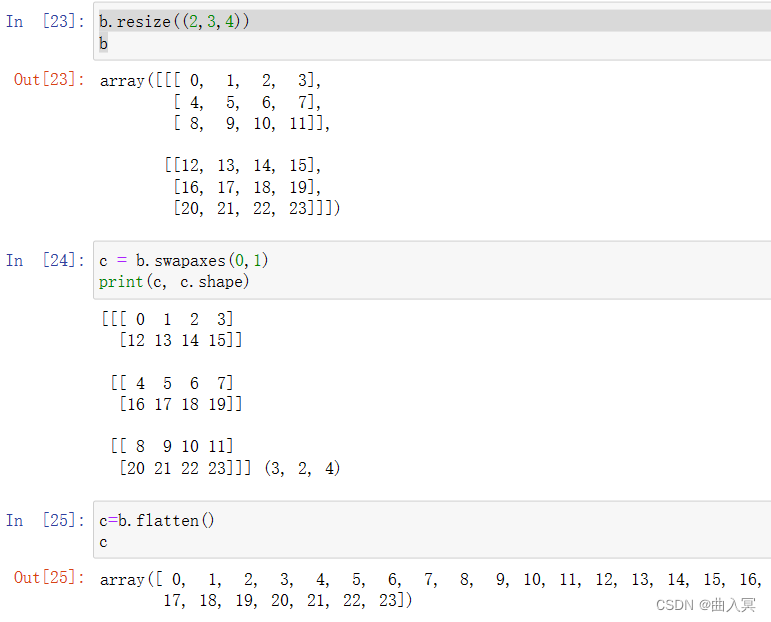
ndarray数组的类型变换
new_a = a.astype(new_type)

4.ndarray数组的操作
4.1 数组的索引和切片
索引:获取数组中特定位置元素的过程
切片:获取数组元素子集的过程
一维数组的索引和切片:与Python的列表类似,正序、反序、冒号运算符搭配使用。

多维数组的索引:类似列表索引,在方括号中每个维度一个索引值,逗号分割,正序、反序、冒号运算符搭配使用。
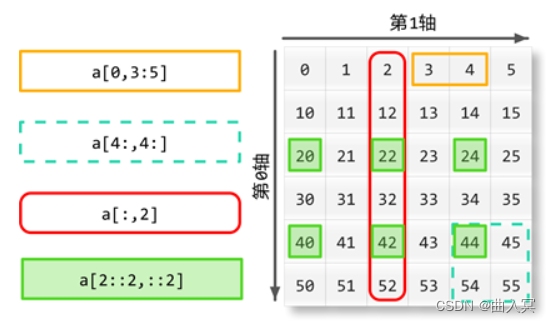

numpy的多维数组和一维数组类似。多维数组有多个轴。从内到外分别是第0轴,第1轴…
多维数组的切片:类似列表切片,在方括号中每个维度一个索引值,逗号分割,正序、反序、冒号运算符搭配使用。
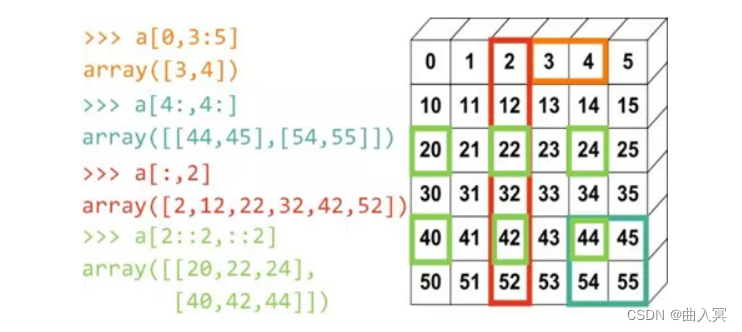
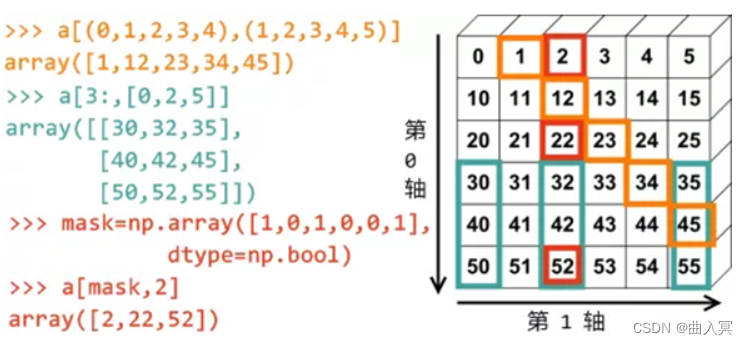
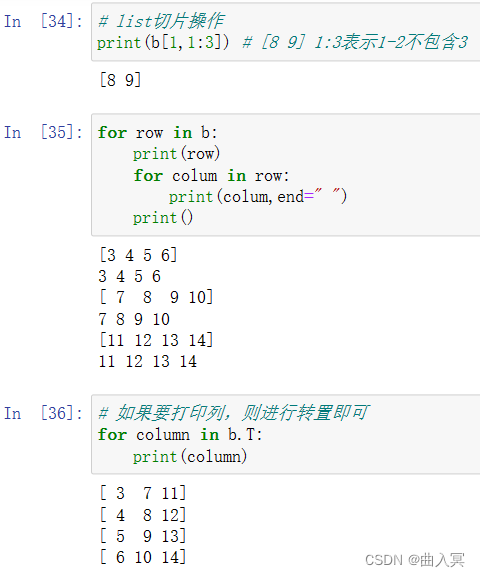
4.2 ndarray数组的运算
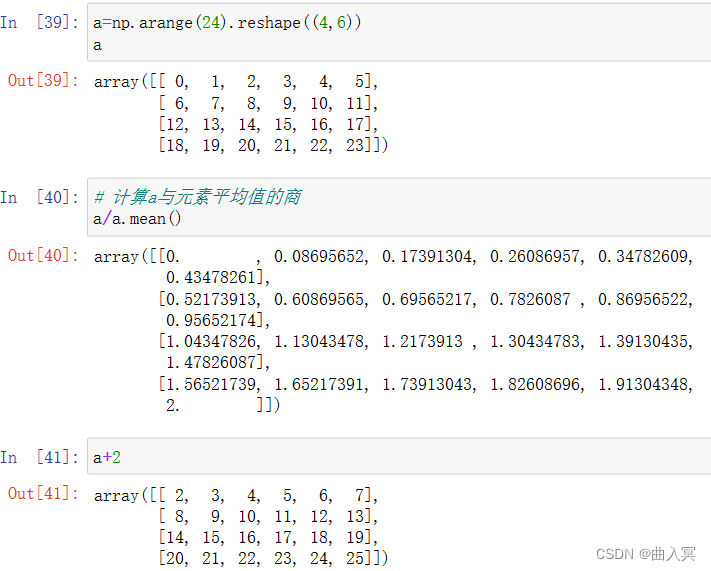
4.2.1 数组与标量的计算
数组与标量之间的运算作用于数组的每一个元素
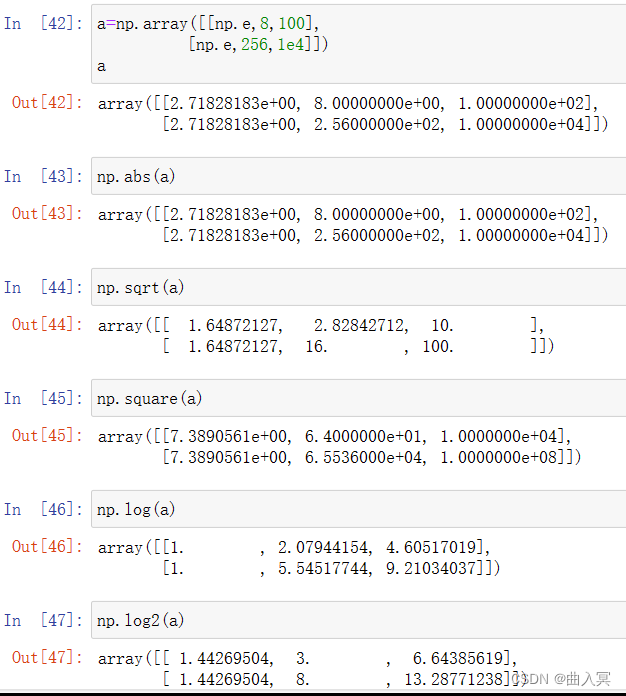
4.2.2 numpy一元函数
对ndarray中的数据执行元素级运算的函数
| 函数 | 说明 |
|---|---|
| np.abs(x) | np.fabs(x)计算数组各元素的绝对值 |
| np.sqrt(x) | 计算数组各元素的平方根 |
| np.square(x) | 计算数组各元素的平方 |
| np.log(x) | 计算数组各元素的自然对数e为底的对数 |
| np.log2(x) | 计算数组各元素的2为底对数 |
| np.log10(x) | 计算数组各元素的10为底对数 |
| np.ceil(x) | np.floor(x)计算数组各元素的ceiling值或floor值 |
| np.rint(x) | 计算数组各元素的四舍五入值 |
| np.modf(x) | 将数组各元素的小数和整数部分以两个独立数组形式返回 |
| np.cos(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.sin(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.tan(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.cosh(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.sinh(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.tanh(x) | 计算数组各元素的普通型和双曲型三角函数 |
| np.exp(x) | 计算数组各元素的指数值 |
| np.sign(x) | 计算数组各元素的符号值,1(+),0,‐1(‐) |

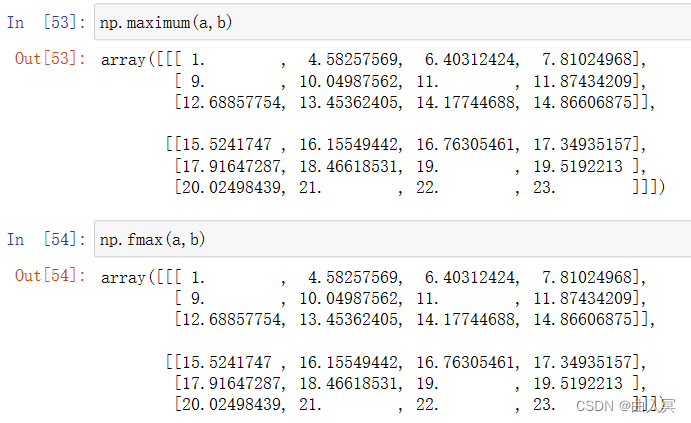
4.2.3 numpy二元函数
| 函数 | 说明 |
|---|---|
| + - * / ** | 两个数组各元素进行对应运算 |
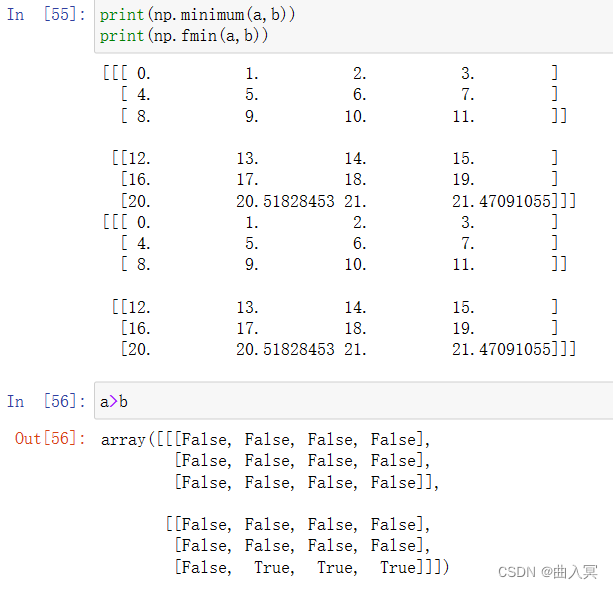
| np.maximum(x,y) | 元素级的最大值/最小值计算 |
| np.minimum(x,y) | 元素级的最大值/最小值计算 |
| np.fmax() | 元素级的最大值/最小值计算 |
| np.fmin() | 元素级的最大值/最小值计算 |
| np.mod(x,y) | 元素级的模运算 |
| np.copysign(x,y) | 将数组y中各元素值的符号赋值给数组x对应元素 |
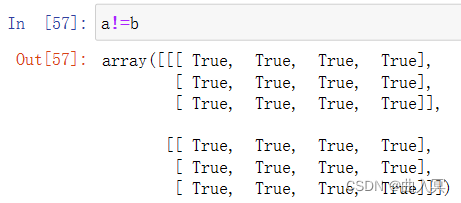
| > < >= <= == != | 算术比较,产生布尔型数组 |

5. numpy广播机制(Broadcasting)
numpy中的基本运算(加、减、乘、除、求余等等)都是元素级别的,但是这仅仅局限于两个数组的形状相同的情况下。如果让一个数组加1的话,结果时整个数组的结果都会加1,这是什么情况?
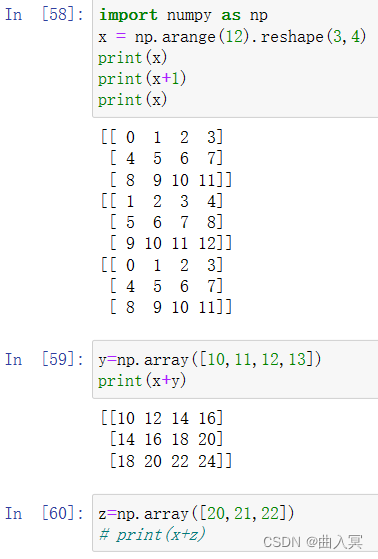
这就是广播机制:numpy 可以转换这些形状不同的数组,使它们都具有相同的大小,然后再对它们进行运算。
在numpy中进行数组运算时,如果两个数组的形状相同,那么两个数组相乘就是两个数组的对应位相乘,这里要求维数相同,并且各维度的长度相同,但是当运算中两个数组的形状不同使时,numpy将会自动触发广播机制。
要了解numpy的广播机制,才能更好的进行数组的运算。
numpy数组间的基础运算是一对一,也就是a.shape==b.shape,但是当两者不一样的时候,就会自动触发广播机制。
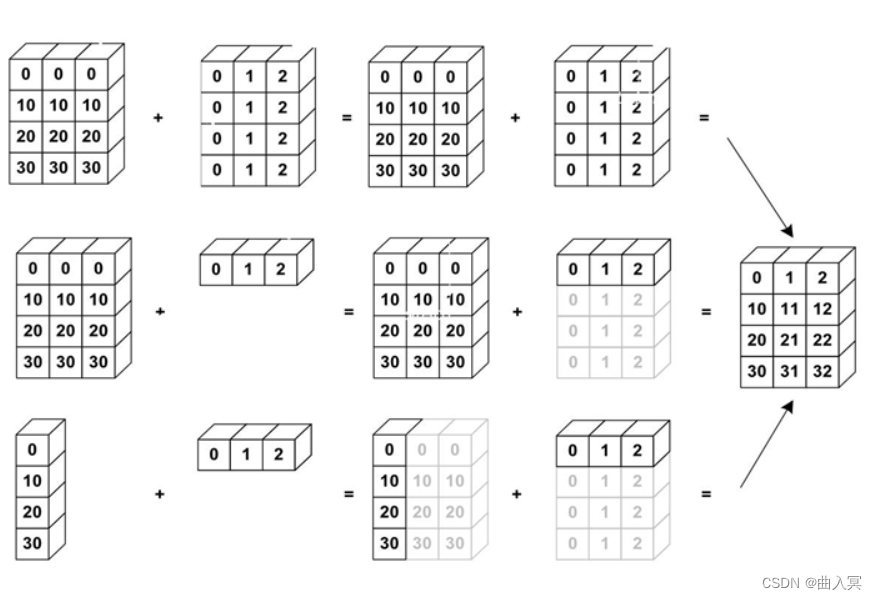
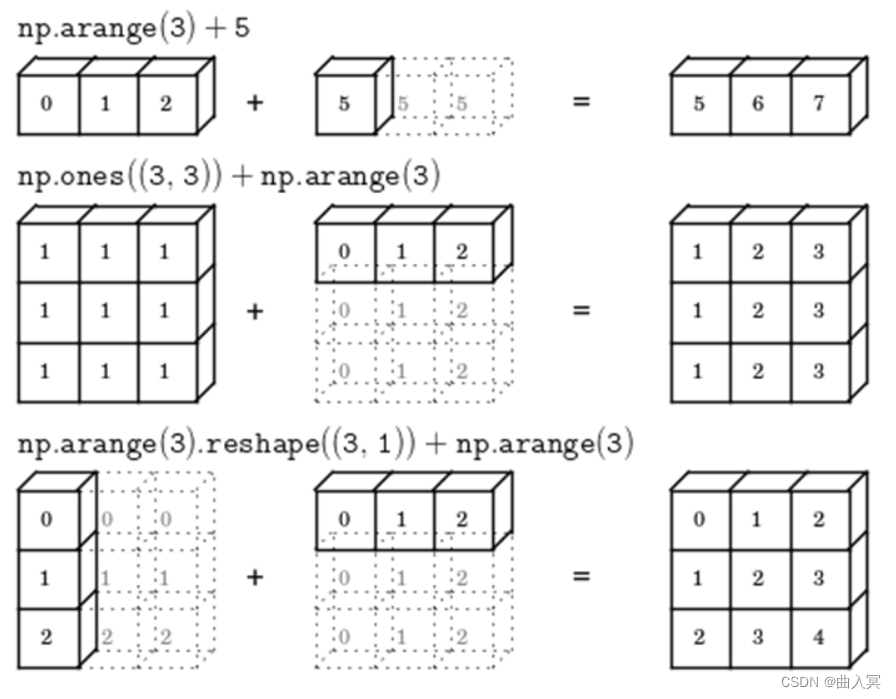
广播是numpy在算术运算期间处理不同形状的数组的能力。对数组的算术运算通常在相应的元素上进行。如果两个数组具有完全相同的形状,则这些操作被无缝执行。
如果两个数组的维数不相同,则元素到元素的操作是不可能的。在 numpy 中仍然可以对形状不相似的数组进行操作,较小的数组会广播到较大数组的大小,以便使它们的形状可兼容。
6. numpy的运算及函数库
6.1 ufunc函数
ufunc是universal function的简称,它是一种能对数组每个元素进行运算的函数。numpy的许多ufunc函数都是用C语言实现的,因此它们的运算速度非常快。
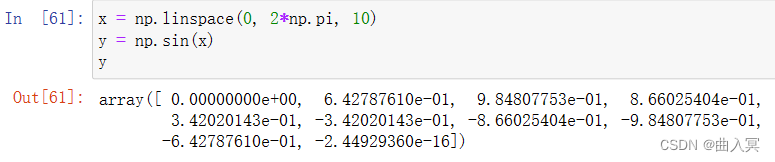
值得注意的是,对于同等长度的ndarray,np.sin()比math.sin()快,但是对于单个数值,math.sin()的速度则更快。
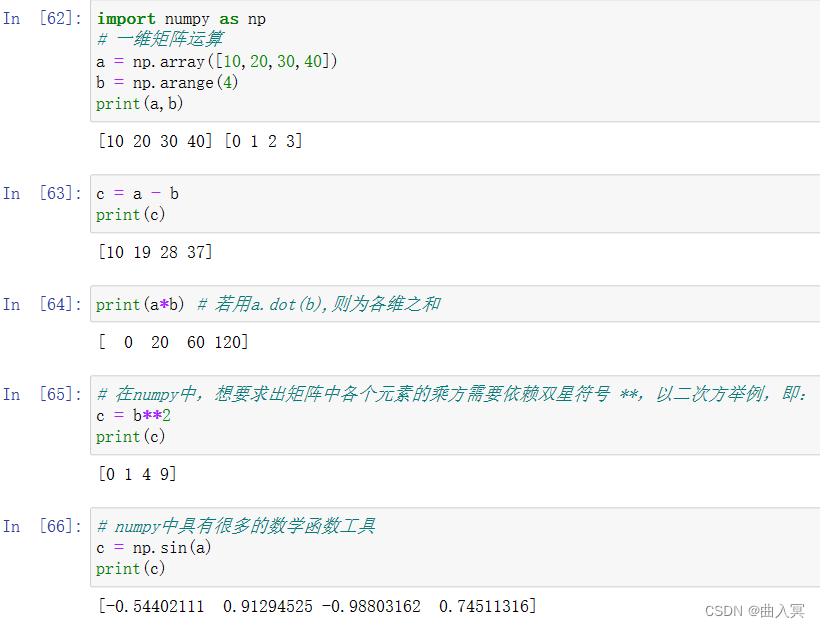
6.1.1 四则运算
numpy提供了许多ufunc函数,它们和相应的运算符运算结果相同。
算术运算符:+ - * / % **
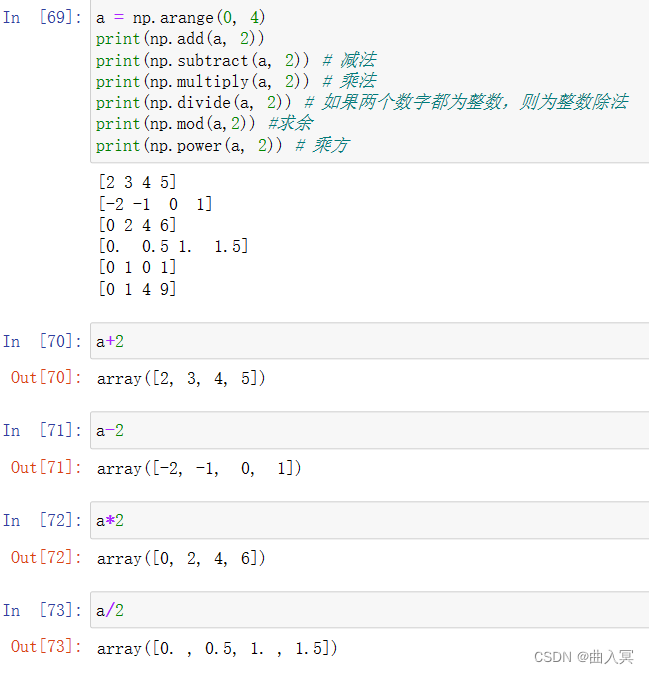

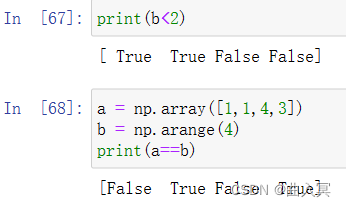
6.1.2 关系运算和布尔运算
使用关系运算符“>、<、>=、<=、==、!=”对两个数组进行比较,会返回一个布尔数组,每一个元素都是对应元素的比较结果。
布尔运算在numpy中也有对应的ufunc函数。

| 表达式 | ufunc函数 |
|---|---|
| x1==x2 | np.equal(x1,x2) |
| x1!=x2 | np.not_equal(x1,x2) |
| x1<x2 | np.less(x1,x2) |
| x1<=x2 | np.not_equak(x1,x2) |
| x1>x2 | np.greater(x1,x2) |
| x1>=x2 | np.gerater_equal(x1,x2) |

6.2 numpy的随机数函数
numpy产生随机数的模块在random里面,其中有大量的分布。
numpy的random子库
np.random.*
np.random.rand();np.random.randn();np.random.randint()
| 函数 | 说明 |
|---|---|
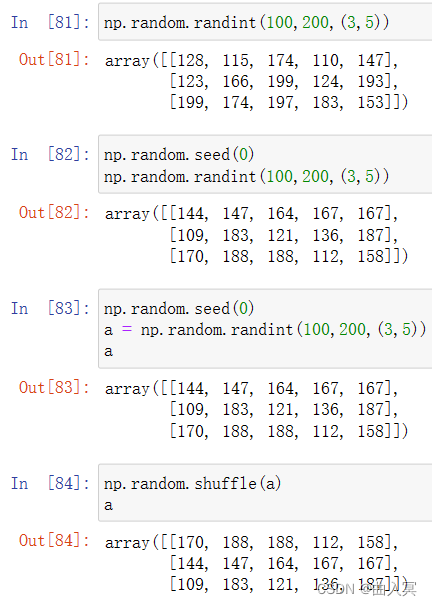
| seed(s) | 随机数种子,s是给定的种子值 |
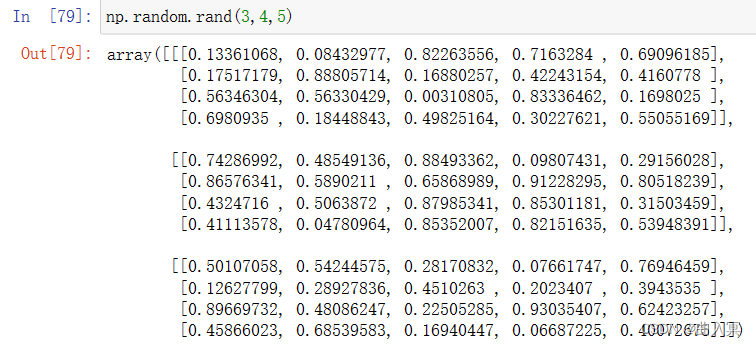
| rand(d0,d1,…,dn) | 根据d0‐dn创建随机数数组,浮点数,[0,1),均匀分布 |
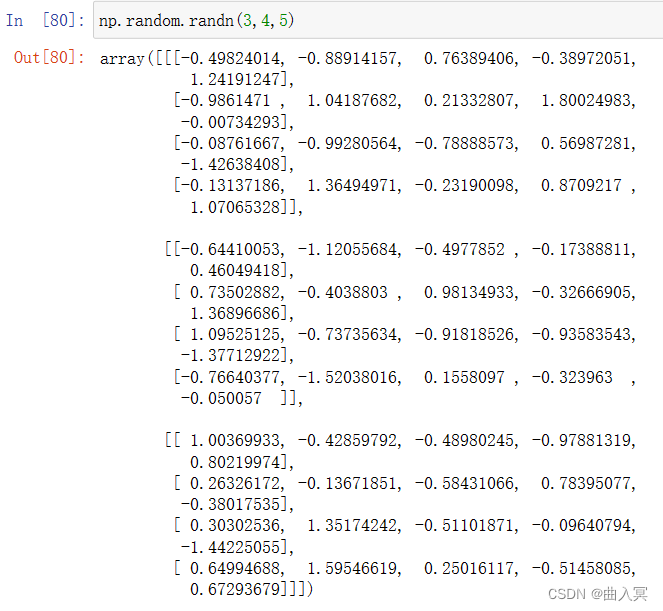
| randn(d0,d1,…,dn) | 根据d0‐dn创建随机数数组,标准正态分布 |
| randint(low[,high,shape]) | 根据shape创建随机整数或整数数组,范围是[low,high) |
| choice(a[,size,replace,p]) | 从一维数组a中以概率p抽取元素,形成size形状新数组 |
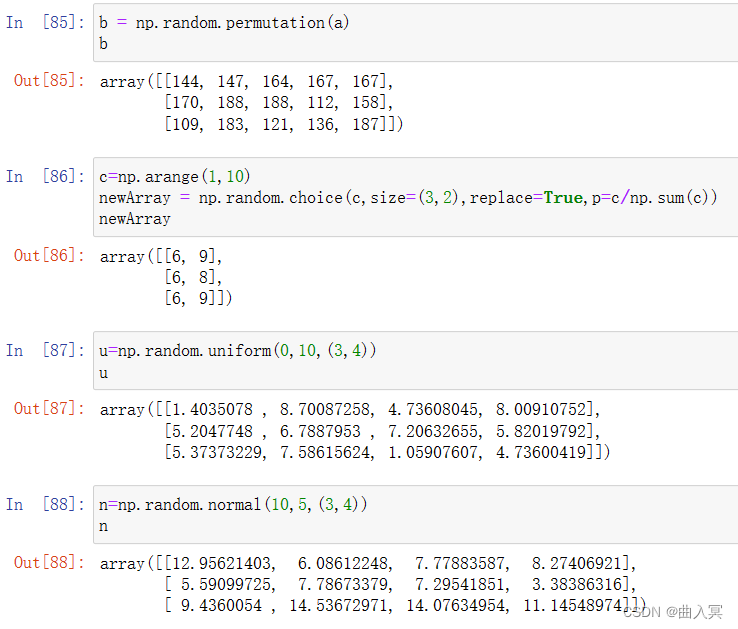
| normal(loc,scale,size) | 产生具有正态分布的数组,loc均值,scale标准差,size形状 |
| uniform(low,high,size) | 产生具有均匀分布的数组,low起始值,high结束值,size形状,replace表示是否可以重用元素,默认为False |
| poisson(lam,size) | 产生具有泊松分布的数组,lam随机事件发生率,size形状 |
| shuffle(a) | 根据数组a的第0轴进行随排列,改变数组x |
| permutation(a) | 根据数组a的第1轴产生一个新的乱序数组,不改变数组x |
6.3 numpy的统计函数
numpy直接提供的统计类函数(np.*):
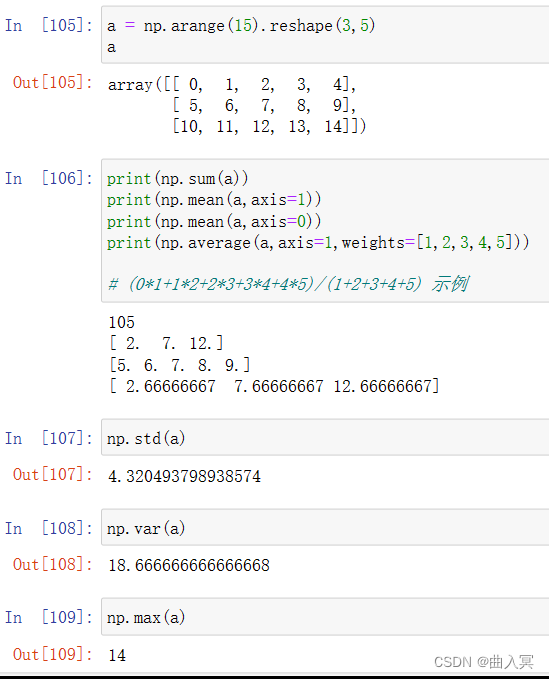
np.std()
np.var()
np.average()
| 函数 | 说明 |
|---|---|
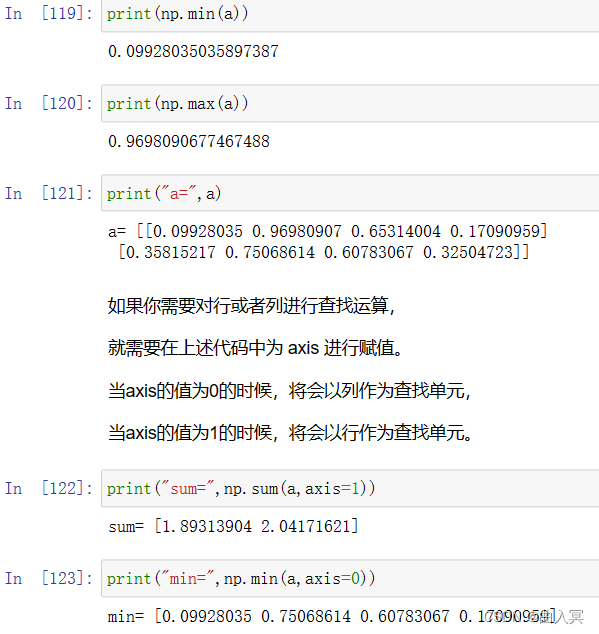
| sum(a,axis=None) | 根据给定轴axis计算数组a相关元素之和,axis整数或元组 |
| mean(a,axis=None) | 根据给定轴axis计算数组a相关元素的期望,axis整数或元组 |
| average(a,axis=None,weights=None) | 根据给定轴axis计算数组a相关元素的加权平均值 |
| std(a,axis=None) | 根据给定轴axis计算数组a相关元素的标准差 |
| var(a,axis=None) | 根据给定轴axis计算数组a相关元素的方差 |
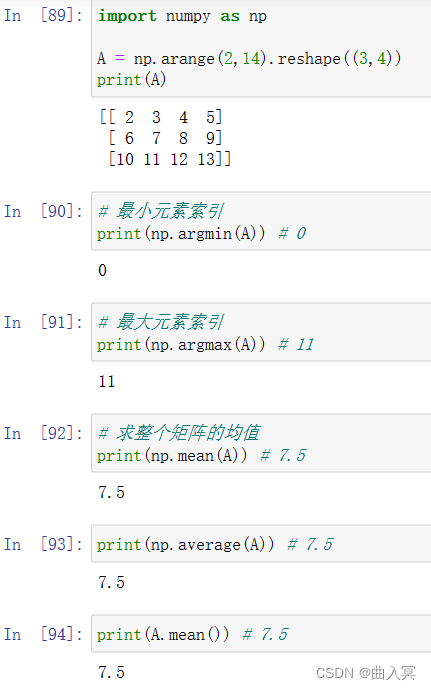
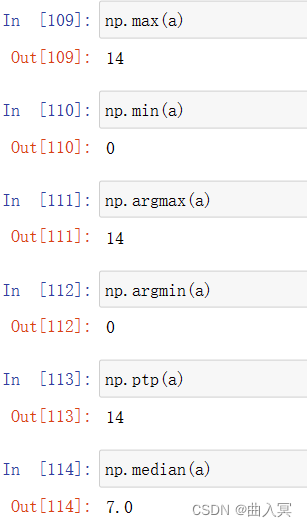
| min(a)max(a) | 计算数组a中元素的最小值、最大值 |
| argmin(a)argmax(a) | 计算数组a中元素最小值、最大值的降一维后下标 |
| unravel_index(index,shape) | 根据shape将一维下标index转换成多维下标 |
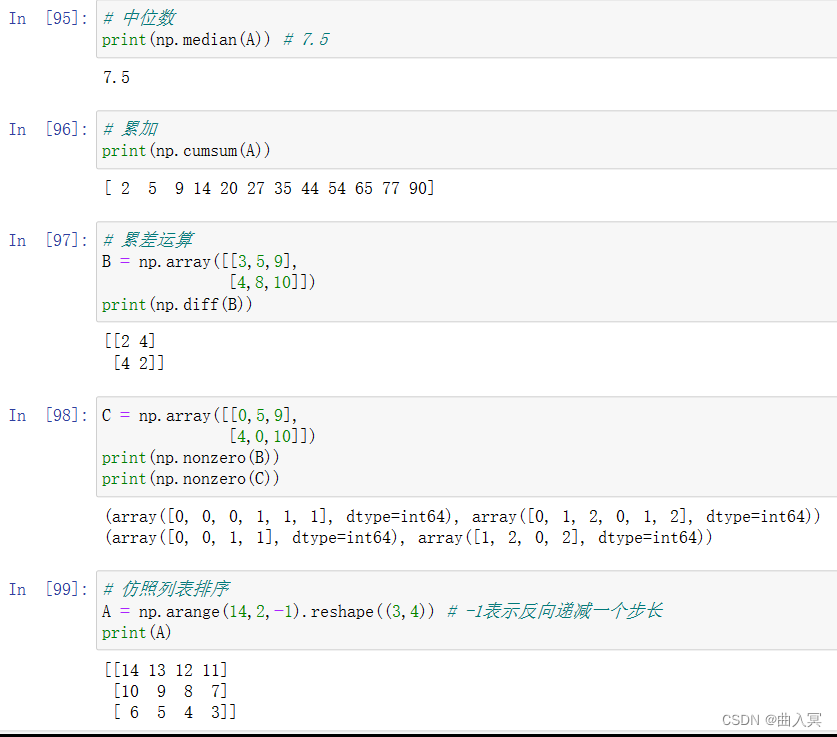
| ptp(a) | 计算数组a中元素最大值与最小值的差 |
| median(a) | 计算数组a中元素的中位数(中值) |
| product | 连乘积 |
| maxinum | 二元最大值 |
| mininum | 二元最小值 |
| sort | 数组排序 |
| percentile | 分位数 |
| argsort | 数组排序下标 |

clip(Array,Array_min,Array_max)
将Array_min<X<Array_max X表示矩阵A中的数,如果满足上述关系,则原数不变。
否则,如果X<Array_min,则将矩阵中X变为Array_min;
如果X>Array_max,则将矩阵中X变为Array_max.
6.4 多维矩阵运算

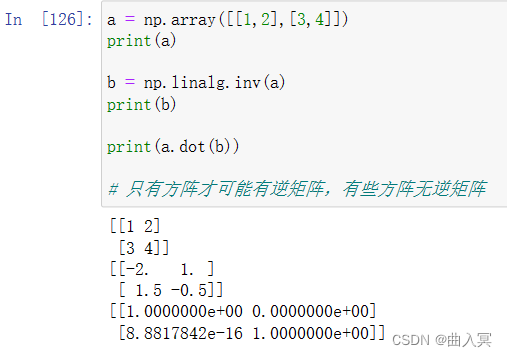
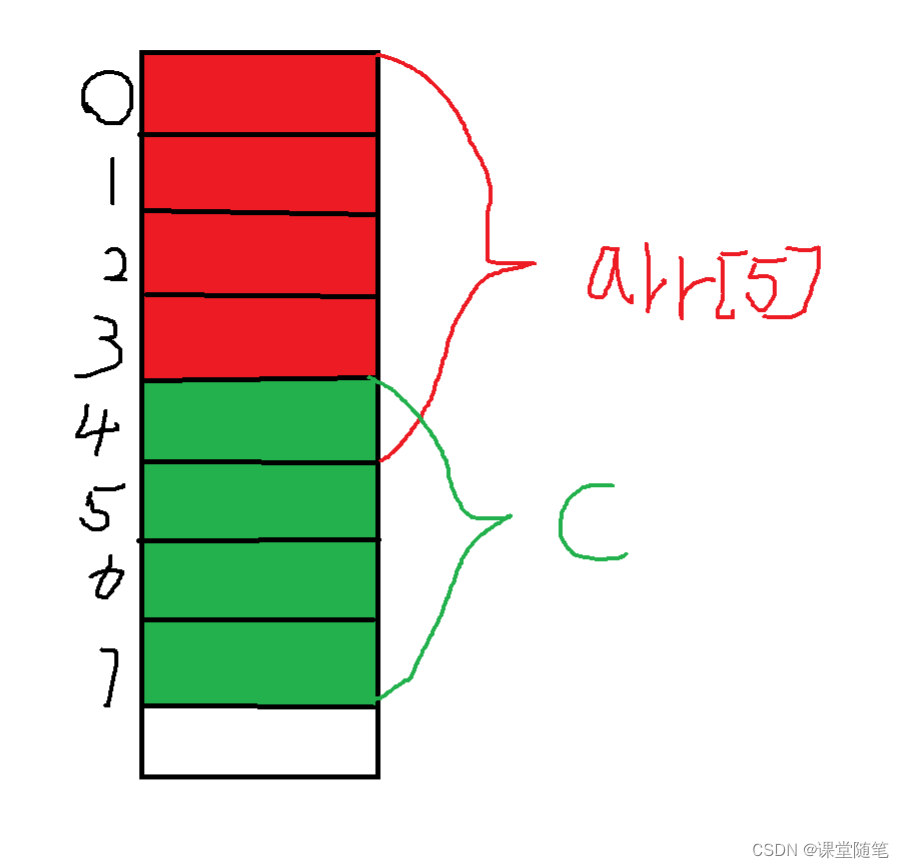
6.5 numpy array合并
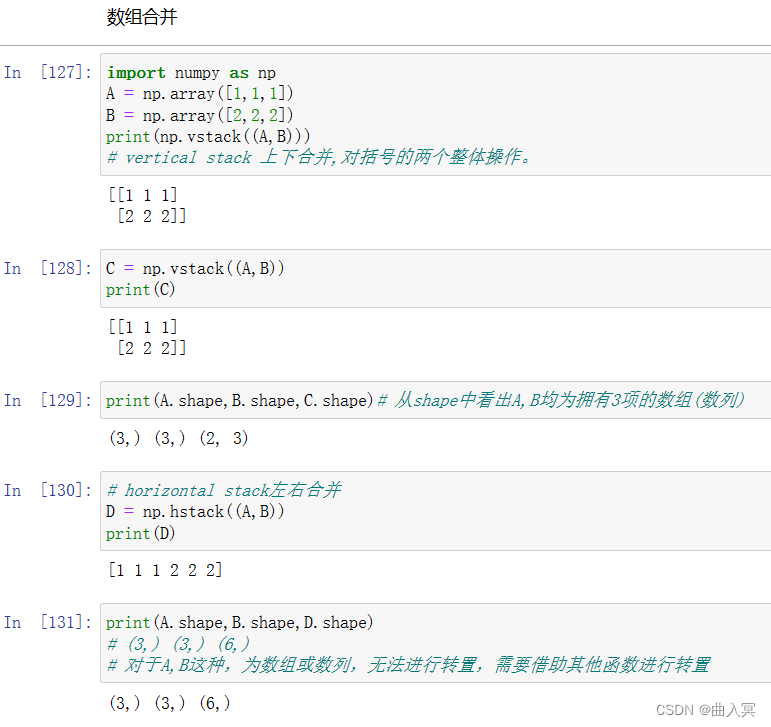

多个矩阵合并:

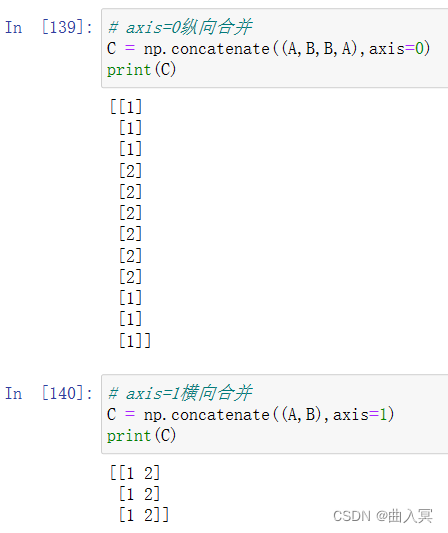
合并示例:
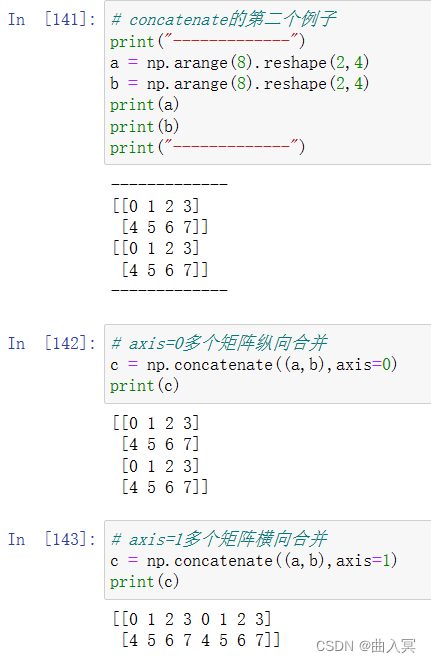
6.6 numpy array分割
构造3行4列矩阵
import numpy as np
A = np.arange(12).reshape((3,4))
print(A)
输出结果:
[[ 0 1 2 3][ 4 5 6 7][ 8 9 10 11]]
等量分割:

不等量分割

其他分割方式

6.7 numpy copy与 =
赋值方式会带有关联性

copy()赋值方式没有关联性

6.8 其它常用函数
np.bincount()
x = np.array([1, 2, 3, 3, 0, 1, 4])
np.bincount(x)
输出结果:
array([1, 2, 1, 2, 1], dtype=int64)
统计索引出现次数:索引0出现1次,1出现2次,2出现1次,3出现2次,4出现1次
因此通过bincount计算出索引出现次数如下:
上面怎么得到的?
对于bincount计算吗,bin的数量比x中最大数多1,例如x最大为4,那么bin数量为5(index从0到4),也就会bincount输出的一维数组为5个数,bincount中的数又代表什么?代表的是它的索引值在x中出现的次数!
还是以上述x为例子,当我们设置weights参数时候,结果又是什么?
这里假定:
w = np.array([0.3,0.5,0.7,0.6,0.1,-0.9,1])
那么设置这个w权重后,结果为多少?
np.bincount(x,weights=w)
输出结果:
array([ 0.1, -0.6, 0.5, 1.3, 1. ])
怎么计算的?
先对x与w抽取出来:
x ---> [1, 2, 3, 3, 0, 1, 4]
w ---> [0.3,0.5,0.7,0.6,0.1,-0.9,1]
索引 0 出现在x中index=4位置,那么在w中访问index=4的位置即可,w[4]=0.1
索引 1 出现在x中index=0与index=5位置,那么在w中访问index=0与index=5的位置即可,然后将两这个加和,计算得:w[0]+w[5]=-0.6
其余的按照上面的方法即可!
bincount的另外一个参数为minlength,这个参数简单,可以这么理解,当所给的bin数量多于实际从x中得到的bin数量后,后面没有访问到的设置为0即可。
还是上述x为例:
这里我们直接设置minlength=7参数,并输出!
np.bincount(x,weights=w,minlength=7)
输出结果:
array([ 0.1, -0.6, 0.5, 1.3, 1. , 0. , 0. ])
与上面相比多了两个0,这两个怎么会多?
上面知道,这个bin数量为5,index从0到4,那么当minlength为7的时候,也就是总长为7,index从0到6,多了后面两位,直接补位为0即可!
np.argmax()
函数原型为:numpy.argmax(a, axis=None, out=None).
函数表示返回沿轴axis最大值的索引。
x = [[1,3,3],[7,5,2]]
print(np.argmax(x))
#输出结果:3
对于这个例子我们知道,7最大,索引位置为3(这个索引按照递增顺序)!
axis属性
axis=0表示按列操作,也就是对比当前列,找出最大值的索引!
x = [[1,3,3],[7,5,2]]
print(np.argmax(x,axis=0))
#输出结果:[1 1 0]
axis=1表示按行操作,也就是对比当前行,找出最大值的索引!
x = [[1,3,3],[7,5,2]]
print(np.argmax(x,axis=0))
#输出结果:[1 1 0]
那如果碰到重复最大元素?
返回第一个最大值索引即可!
例如:
x = np.array([1, 3, 2, 3, 0, 1, 0])
print(x.argmax())
#输出:1
上述合并实例
这里来融合上述两个函数,举个例子:
x = np.array([1, 2, 3, 3, 0, 1, 4])
print(np.argmax(np.bincount(x)))
#输出:1
最终结果为1,为什么?
首先通过np.bincount(x)得到的结果是:[1 2 1 2 1],再根据最后的遇到重复最大值项,则返回第一个最大值的index即可!2的index为1,所以返回1。
求取精度
np.around([-0.6,1.2798,2.357,9.67,13], decimals=0)#取指定位置的精度
#输出结果:array([-1., 1., 2., 10., 13.])
看到没,负数进位取绝对值大的!
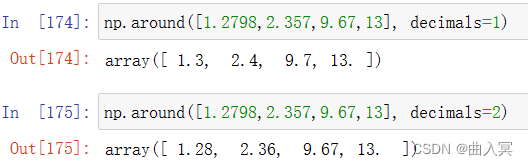
从上面可以看出,decimals表示指定保留有效数的位数,当超过5就会进位(此时包含5)!
但是,如果这个参数设置为负数,又表示什么?
np.around([1,2,5,6,56], decimals=-1)
#输出结果:array([ 0, 0, 0, 10, 60])
发现没,当超过5时候(不包含5),才会进位!-1表示看一位数进位即可,那么如果改为-2呢,那就得看两位!
np.around([1,2,5,50,56,190], decimals=-2)
#输出结果:array([ 0, 0, 0, 0, 100, 200])
看到没,必须看两位,超过50才会进位,190的话,就看后面两位,后两位90超过50,进位,那么为200!
计算沿指定轴第N维的离散差值

取整

看到没,负数取整,跟上述的around一样,是向左!
取上限

取上限!找这个小数的最大整数即可!
查找
利用np.where实现小于0的值用0填充吗,大于0的数不变!

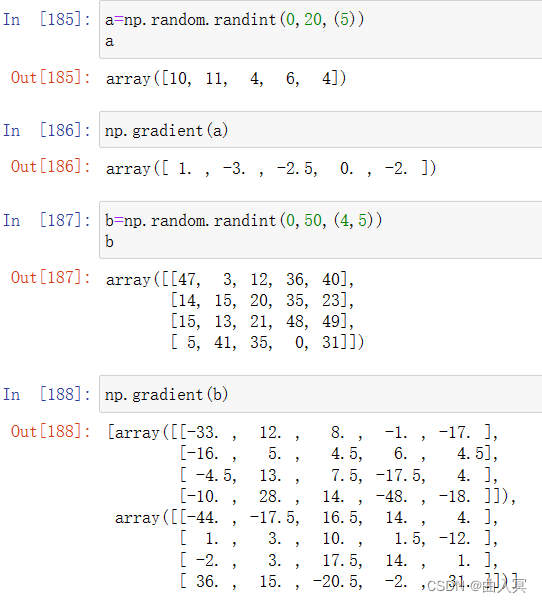
numpy的梯度函数
| 函数 | 说明 |
|---|---|
| np.gradient(f) | 计算数组f中元素的梯度,当f为多维时,返回每个维度梯度 |
梯度:连续值之间的变化率,即斜率
XY坐标轴连续三个X坐标对应的Y轴值:a, b, c,其中,b的梯度是: (c‐a)/2
7. numpy文件存取
7.1 CSV文件的存取
CSV (Comma‐Separated Value, 逗号分隔值),它是一种常见的文件格式,用来存储批量数据。
CSV文件的保存:
np.savetxt(frame, array, fmt=‘%.18e’, delimiter=None)
- frame : 文件、字符串或产生器,可以是.gz或.bz2的压缩文件
- array : 存入文件的数组
- fmt : 写入文件的格式,例如:%d %.2f %.18e
- delimiter : 分割字符串,默认是任何空格

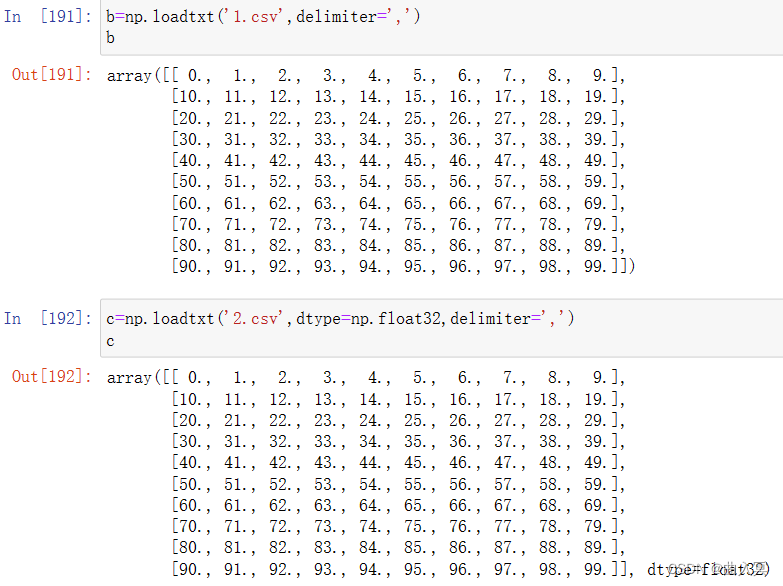
CSV文件的读取:
np.loadtxt(frame, dtype=np.float32, delimiter=None, unpack=False)
-
frame : 文件、字符串或产生器,可以是.gz或.bz2的压缩文件
-
dtype : 数据类型,可选
-
delimiter : 分割字符串,默认是任何空格
-
unpack : 如果True,读入属性将分别写入不同变量
CSV文件的局限性: -
CSV只能有效存储一维和二维数组;
-
np.savetxt()和np.loadtxt()只能有效存取一维和二维数组
7.2 多维数据的存取
文件的保存:
a.tofile(frame, sep=‘’, format=‘%s’)
- frame : 文件、字符串
- sep : 数据分割字符串,如果是空串,写入文件为二进制
- format : 写入数据的格式
a.tofile('1.txt',sep=',',format='%d')
文件的读取:
np.fromfile(frame, dtype=float, count=‐1, sep=‘’)
- frame : 文件、字符串
- dtype : 读取的数据类型
- count : 读入元素个数,‐1表示读入整个文件
- sep : 数据分割字符串,如果是空串,写入文件为二进制
d=np.fromfile('1.txt',dtype=np.float32,sep=',')
d
输出结果:
array([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12.,13., 14., 15., 16., 17., 18., 19., 20., 21., 22., 23., 24., 25.,26., 27., 28., 29., 30., 31., 32., 33., 34., 35., 36., 37., 38.,39., 40., 41., 42., 43., 44., 45., 46., 47., 48., 49., 50., 51.,52., 53., 54., 55., 56., 57., 58., 59., 60., 61., 62., 63., 64.,65., 66., 67., 68., 69., 70., 71., 72., 73., 74., 75., 76., 77.,78., 79., 80., 81., 82., 83., 84., 85., 86., 87., 88., 89., 90.,91., 92., 93., 94., 95., 96., 97., 98., 99.], dtype=float32)
该方法需要读取时知道存入文件时数组的维度和元素类型,a.tofile()和np.fromfile()需要配合使用。
7.3 numpy的便捷文件存取
保存:
np.save(fname, array) 或np.savez(fname, array)
- fname : 文件名,以.npy为扩展名,压缩扩展名为.npz
- array : 数组变量
读取:
np.load(fname)
- fname : 文件名,以.npy为扩展名,压缩扩展名为.npz
np.save('a.npy',a)
b=np.load('a.npy')
b
输出结果:
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],[20, 21, 22, 23, 24, 25, 26, 27, 28, 29],[30, 31, 32, 33, 34, 35, 36, 37, 38, 39],[40, 41, 42, 43, 44, 45, 46, 47, 48, 49],[50, 51, 52, 53, 54, 55, 56, 57, 58, 59],[60, 61, 62, 63, 64, 65, 66, 67, 68, 69],[70, 71, 72, 73, 74, 75, 76, 77, 78, 79],[80, 81, 82, 83, 84, 85, 86, 87, 88, 89],[90, 91, 92, 93, 94, 95, 96, 97, 98, 99]])