JAVA代码编写
70. 爬楼梯(进阶版)
卡码网:57. 爬楼梯(第八期模拟笔试)
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述
输入共一行,包含两个正整数,分别表示n, m
输出描述
输出一个整数,表示爬到楼顶的方法数。
输入示例
3 2
输出示例
3
提示信息
数据范围:
1 <= m < n <= 32;
当 m = 2,n = 3 时,n = 3 这表示一共有三个台阶,m = 2 代表你每次可以爬一个台阶或者两个台阶。
此时你有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶段
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
教程:https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html#%E6%80%9D%E8%B7%AF
方法一:动态规划
思路:和70. 爬楼梯很像,基础的是每次只能走1个或2个台阶,现在改成能走1-m中任意一个台阶。问有多少种方法走完n阶楼梯。
步骤
-
定义dp数组:dp[j]: 爬到第j层楼梯,有dp[j]种方法
-
递推公式:dp[j] = dp[j - 1] + dp[j - 2] + … +dp[j - m]
- dp[j - 1],上j-1层楼梯,有dp[j - 1]种方法,那么再1步跳一个台阶不就是dp[j]了么。
- dp[j - 2],上j-2层楼梯,有dp[j - 2]种方法,那么再2步跳两个台阶不就是dp[j]了么。
- …
- dp[j - m],上j-m层楼梯,有dp[j - m]种方法,那么再m步跳两个台阶不就是dp[j]了么。
可以这样理解。因为每次只能走1个楼梯或2个楼梯…或m个楼梯,那么我们要走j个楼梯,可以从第j-m个楼梯,再走m个楼梯;…;也可以从第j-1个楼梯,再走1个楼梯。所以dp[j] = dp[j - 1] + dp[j - 2] + … +dp[j - m]
-
dp数组初始化:dp[1]=1,dp[2]=2
-
确定遍历顺序:遍历n,再遍历m
-
举例推导dp数组
n=4,m=2
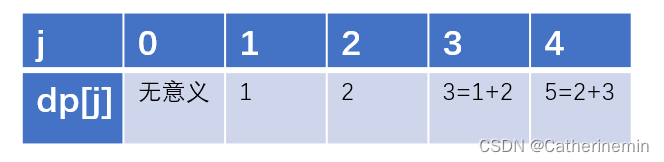
简单来说,dp[j]等于前m个dp的和,这里的dp[4]=dp[3]+dp[2],刚好是2个的和。
复杂度分析:
- 时间复杂度:
O(n * m) - 空间复杂度:
O(n)
import java.util.Scanner;class Solution{public static void main(String [] args){Scanner sc = new Scanner(System.in);int m, n;while (sc.hasNextInt()) {// 从键盘输入参数,中间用空格隔开n = sc.nextInt();m = sc.nextInt();// 求排列问题,先遍历背包再遍历物品int[] dp = new int[n + 1];dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 1; i <= m; i++) {if (j - i >= 0) dp[j] += dp[j - i];}}System.out.println(dp[n]);}}
}
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
提示:
1 <= coins.length <= 121 <= coins[i] <= 231 - 10 <= amount <= 104
教程:https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html
方法一:动态规划
思路:五步曲
步骤
-
定义dp [j]:凑成和为amount的最少硬币个数为dp[j]。
-
递推公式:
凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i])
所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。
递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
-
dp数组初始化:dp[0] =0,考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
-
确定遍历顺序:
本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。
所以本题并不强调集合是组合还是排列。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
-
举例推导dp数组,
以输入:coins = [1, 2, 5], amount = 5为例
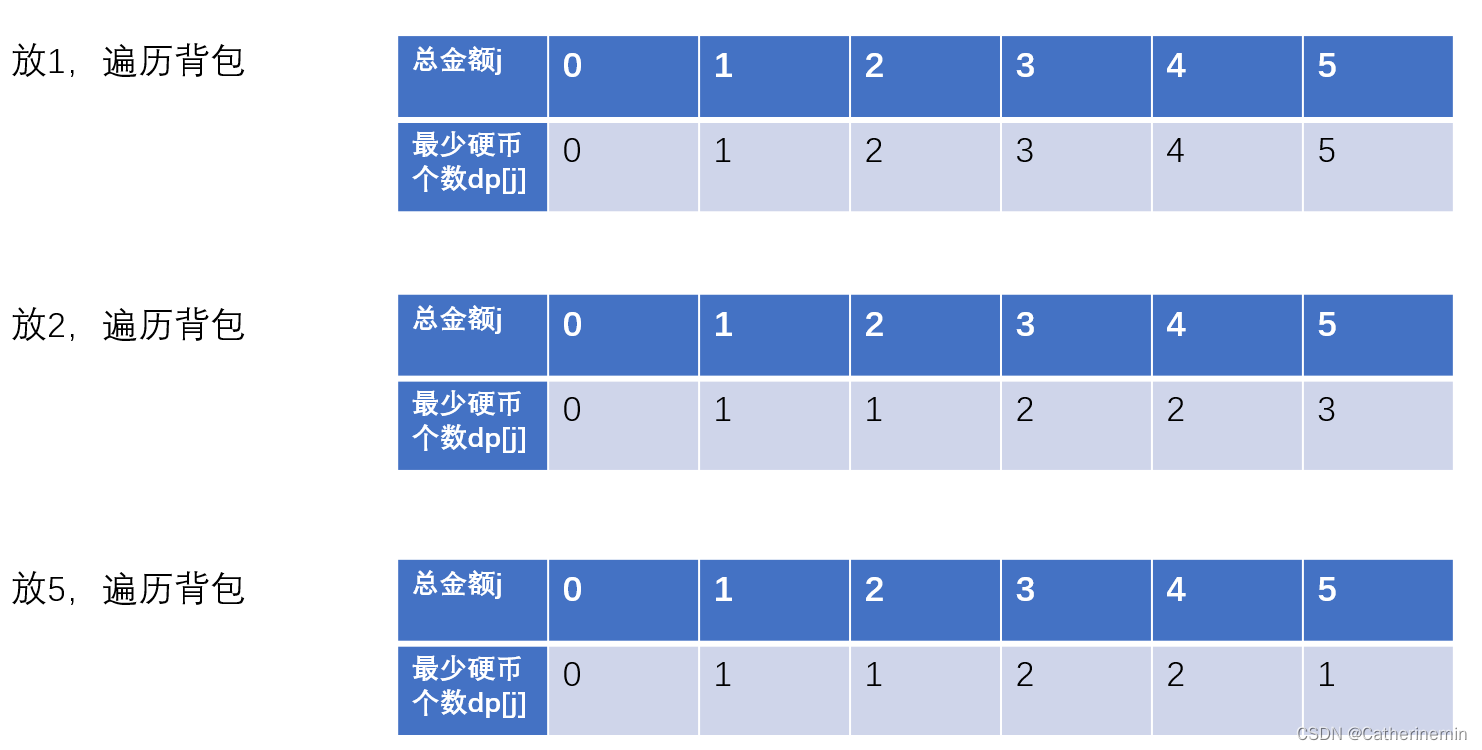
复杂度分析:
- 时间复杂度:
O(n * amount),n 为coins长度 - 空间复杂度:
O(amount)
class Solution {public int coinChange(int[] coins, int amount) {int max = Integer.MAX_VALUE;int[] dp = new int[amount + 1];//初始化dp数组为最大值for (int j = 0; j < dp.length; j++) {dp[j] = max;}//当金额为0时需要的硬币数目为0dp[0] = 0;for (int i = 0; i < coins.length; i++) {//正序遍历:完全背包每个硬币可以选择多次for (int j = coins[i]; j <= amount; j++) {//只有dp[j-coins[i]]不是初始最大值时,该位才有选择的必要if (dp[j - coins[i]] != max) {//选择硬币数目最小的情况dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);}}}return dp[amount] == max ? -1 : dp[amount];}public static void main(String[] args) {Solution solution = new Solution();solution.coinChange(new int[] {1,2,5},5);}
}
从贪心的角度看,每次放最大的硬币,一直放,直到amount剩下为amount%最大硬币值,接着放次大或能直接整除的硬币。
class Solution {public int coinChange(int[] coins, int amount) {if (amount == 0) return 0;if (coins.length == 1 && amount % coins[0] != 0) return -1;int count = 0;Arrays.sort(coins);for (int i = coins.length - 1; i >= 0; i--) {count += amount / coins[i];amount = amount % coins[i];if (amount == 0) {return count;}}return -1;}
}
但是这个代码不能通过,贪心不能通过局部最优获取全局最优。
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
教程:https://programmercarl.com/0279.%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0.html#_279-%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0
方法一:动态规划
思路:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
完全背包
步骤
-
定义dp [j]:和为j的完全平方数的最少数量为dp[j]。
-
递推公式:
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
-
dp数组初始化:dp[0] =0,dp[j]赋最大值
-
确定遍历顺序:
两者都可:
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
-
举例推导dp数组,
已输入n为5例,dp状态图如下:

复杂度分析:
- 时间复杂度:
O(n*sqrt(n)) - 空间复杂度:
O(n)
class Solution {// 版本一,先遍历物品, 再遍历背包public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];//初始化for (int j = 0; j <= n; j++) {dp[j] = max;}//如果不想要寫for-loop填充數組的話,也可以用JAVA內建的Arrays.fill()函數。//Arrays.fill(dp, Integer.MAX_VALUE);//当和为0时,组合的个数为0dp[0] = 0;// 遍历物品for (int i = 1; i * i <= n; i++) {// 遍历背包for (int j = i * i; j <= n; j++) {//if (dp[j - i * i] != max) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);//}//不需要這個if statement,因爲在完全平方數這一題不會有"湊不成"的狀況發生( 一定可以用"1"來組成任何一個n),故comment掉這個if statement。}}return dp[n];}
}class Solution {// 版本二, 先遍历背包, 再遍历物品public int numSquares(int n) {int max = Integer.MAX_VALUE;int[] dp = new int[n + 1];// 初始化for (int j = 0; j <= n; j++) {dp[j] = max;}// 当和为0时,组合的个数为0dp[0] = 0;// 遍历背包for (int j = 1; j <= n; j++) {// 遍历物品for (int i = 1; i * i <= j; i++) {dp[j] = Math.min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
}

![NSS [NSSCTF 2022 Spring Recruit]babyphp](https://img-blog.csdnimg.cn/img_convert/6ce9f9695f4bb748a261dd4dff661196.png)