二叉树的概念

1.二叉树的性质：

二叉树的每个节点最多有两个子节点，分别称为左孩子、右孩子，以他们为根的子树称为左子树、右子树。

二叉树的每层节点数以 2 的倍数递增，所以二叉树的第 i 层最多有   个节点。如果每层的节点数都是满的，称它为满二叉树。一个 n 层的满二叉树，一共有  个节点。如果满二叉树只在最后一层有缺失，并且缺失的编号都在最后，则称为完全二叉树。

 2.二叉树的存储结构

二叉树的一个节点的存储，包括节点的值、左右子节点，有动态和静态两种存储方法。

（1）动态二叉树。在数据结构中一般这样定义：

struct node
{int value;//节点的值，可以定义多个值node *left,*right;//指向左右子节点
};

动态新建一个node时，用new运算符动态申请一个节点。使用完毕后，用delete释放，否则会产生内存泄漏。动态二叉树的优点是不浪费空间，缺点是需要管理，不小心会出错。

（2）用静态数组存储二叉树。在算法竞赛中，为了编码简单，加快速度，一般用静态数组实现二叉树。下面定义一个大小为 N 的结构体数组。

struct node
{//静态二叉树char value;int left,right;//可以简写成l,r
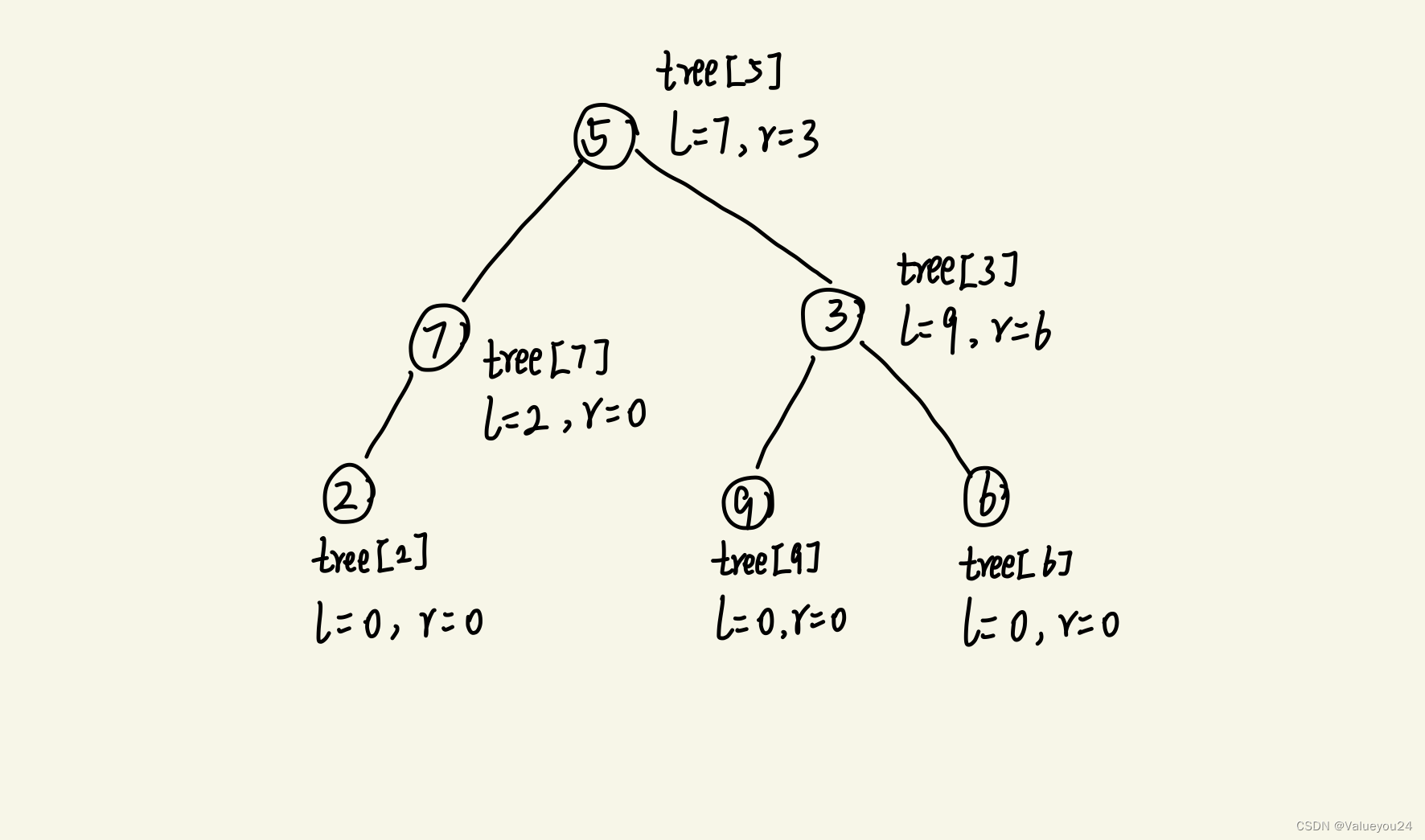
}tree[N];

如下图所示为一颗二叉树的静态存储，根是 tree[ 5 ]。编码时一般不用 tree[ 0 ]，因为 0 被用来表示空节点，如叶子节点 tree[ 2 ] 没有子节点，就把它的子节点赋值为 l = r = 0。

特别地，用数组实现完全二叉树，访问非常便捷，此时连 left、right 都不需要定义。一颗节点总数量为 k 的完全二叉树，设 1 号节点为根节点，有以下性质：

        （1）编号 i > 1 的节点，其父节点编号是 i / 2；

        （2）如果 2i > k，那么节点 i 没有孩子；如果 2i + 1 > k，那么节点 i 没有右孩子；

        （3）如果节点 i 有孩子，那么它的左孩子是节点 2i，右孩子是节点 2i + 1。

3.二叉树的遍历

（1）宽度优先遍历

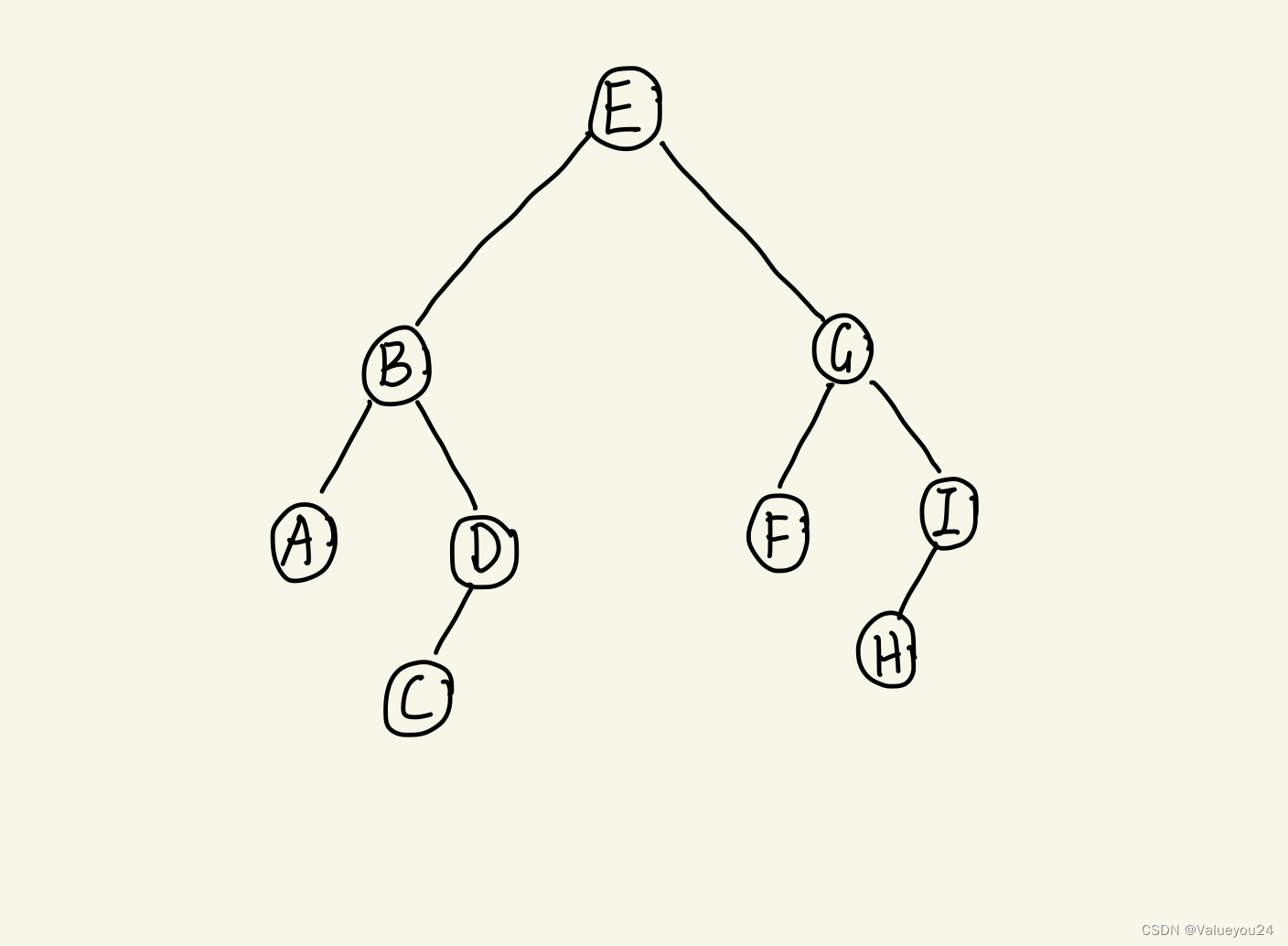
有时需要按层次一层层从上到下遍历二叉树。例如下图，需要按照 E-BG-ADFI-CH 的顺序访问，此时用宽度优先遍历（BFS）是最合适的。

（2）深度优先遍历

用深度优先搜索（DFS）遍历二叉树，代码较为简单，而且产生了许多应用。

按照深度搜索的顺序访问二叉树，对父节点、左孩子、右孩子进行组合，有先序遍历、中序遍历、后序遍历这 3 种访问顺序，这里默认左孩子在右孩子的前面。

       （1）先序遍历，按父节点、左孩子、右孩子的顺序访问，在上图中，先序遍历输出的结果为EBADCGFIH,先序遍历的第一个节点是根。

void preorder(node *root)
{cout << root->value;preorder(root->left);//递归左子树preorder(root->right);//递归右子树
}

        （2）中序遍历，按左孩子、父节点、右孩子的顺序访问。在上图中，中序遍历输出的顺序是ABCDEFGHI。

void inorder(node *root)
{inorder(root->left);//递归左子树cout << root->value;//输出inorder(root->right);//递归右子树
}

        （3）后序遍历，按左孩子、右孩子、父节点的顺序访问。上图中二叉树的后序遍历为ACDBFHIGE。后序遍历的最后一个节点是根节点

void postorder(node *root)
{postorder(root->left);//递归左子树postorder(root->right);//递归右子树cout << root->value;
}

如果已知某课二叉树的中序遍历和另一种遍历，就可以唯一确定一颗二叉树，即“中序+先序”或“中序+后序”，都能确定一颗树。

但是，如果不知道中序遍历，只有先序遍历+后序遍历，则不能唯一确定一颗二叉树