目录
分块
分块算法步骤:
树状数组
树状数组步骤:
线段树点更新
点更新步骤:
线段树区间更新
区间更新步骤:
不同于倍增和前缀和与差分序列。
前缀和处理不更新的区间和
差分处理离线的区间更新问题
倍增处理离线的区间最值问题
分块,树状数组,线段树:
分块处理求多次区间更新的区间和(在线算法)
树状数组求多次点更新的区间和 (在线算法)
线段树求多次点更新或区间更新的区间最值 (在线算法)
分块
分块算法思想:基于优化后的暴力。
分块的本质就是维护每个块的suf数组(和lz),然后分整个块处理和非整个块暴力处理!
分块操作是修改原数组及懒标,维护suf
题目:(POJ 3648) 一个简单的整数问题

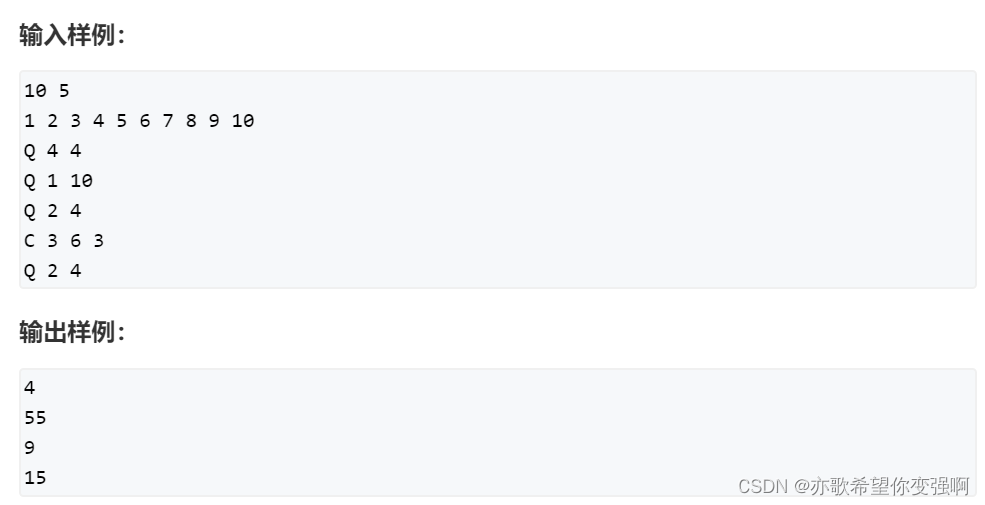
分块算法步骤:
1,预处理块build:初始化每块的左右下标L[],和R[],每个下标的所属块号be,每块的和suf
2,区间修改update:对于完整的块仅修改懒标lz,不完整的就暴力修改a和suf
3,区间查询query :对于完整的块直接利用懒标lz和suf,不完整的就暴力a和lz
(这里没有什么懒标下放,这又不是求区间max)
#include <bits/stdc++.h>//POJ3648
using namespace std;
const int N=100010;
typedef long long ll;
ll suf[N],lz[N];//分块的本质是维护每个块的suf数组(和lz),然后分整个块处理和非整个块暴力处理(相当于优化后的暴力)
int a[N],L[N],R[N],be[N];
int n,m;
//分块:我们处理下标都是从1开始
void build(){//L[]R[]每块的左右下标,be[]每个下标的所属块号,suf[]每块的和int t=sqrt(n);int num=n/t;if(n%t) num++;//t是块长,num是块数,for(int i=1;i<=num;i++){L[i]=(i-1)*t+1; R[i]=i*t;}R[num]=n;//更改最后一块的右下标for(int i=1;i<=num;i++)for(int j=L[i];j<=R[i];j++){be[j]=i;suf[i]+=a[j];//初始化每点的be和每块的suf}
}
//区间修改
void update (int l,int r,int d){//完整块就修改懒标lz,不完整就修改a,sufint p=be[l],q=be[r];if(p==q){//如果在同一块就暴力修改a和suffor(int i=l;i<=r;i++) a[i]+=d;suf[p]+=d*(r-l+1);}else{//否则:完整的块修改懒标lz,不完整还是暴力a和suffor(int i=p+1;i<=q-1;i++) lz[i]+=d;for(int i=l;i<=R[p];i++) a[i]+=d;suf[p]+=d*(R[p]-l+1);for(int i=L[q];i<=r;i++) a[i]+=d;suf[q]+=d*(r-L[q]+1);}
}ll query(int l,int r){//完整块suf和lz,不完整就a和lzint p=be[l],q=be[r];ll ans=0;if(p==q){//同一块就看a和lzfor(int i=l;i<=r;i++) ans+=a[i];ans+=lz[p]*(r-l+1);}else{//否则:完整就suf+lz,不完整还是a和lzfor(int i=p+1;i<=q-1;i++) ans+=suf[i]+lz[i]*(R[i]-L[i]+1);for(int i=l;i<=R[p];i++) ans+=a[i];for(int i=L[q];i<=r;i++) ans+=a[i];ans+=lz[q]*(r-L[q]+1);}return ans;
}int main(){cin>>n>>m;int l,r,d;char op[3];//不要输入字符,输入字符串for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}build();for(int i=1;i<=m;i++){scanf("%s %d %d",op,&l,&r);if(op[0]=='C'){scanf("%d",&d);update(l,r,d);}else{printf("%lld\n",query(l,r));}}
}
树状数组
树状数组思想:和原数组一一对应,且是通过“二进制 ”分解维护区间
树状数组本质就是创建了一个离散的一维数组c,每个点维护不同区间的前缀和。更新和查询都是离散的
树状数组操作是修改c数组的后继,查询c数组的前驱
c[i]区间维护长度: i末尾有连续的k个0,则c[i]保存的区间长度为2^k,即从a[i]向前的2^k个元素
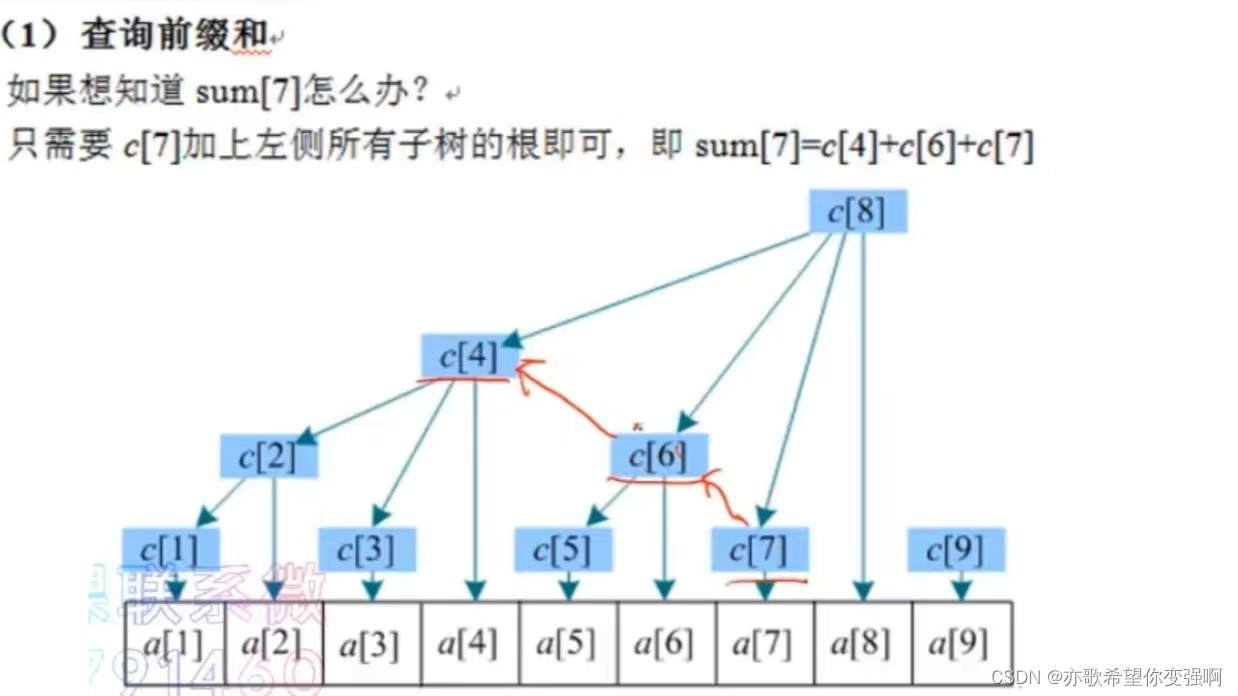
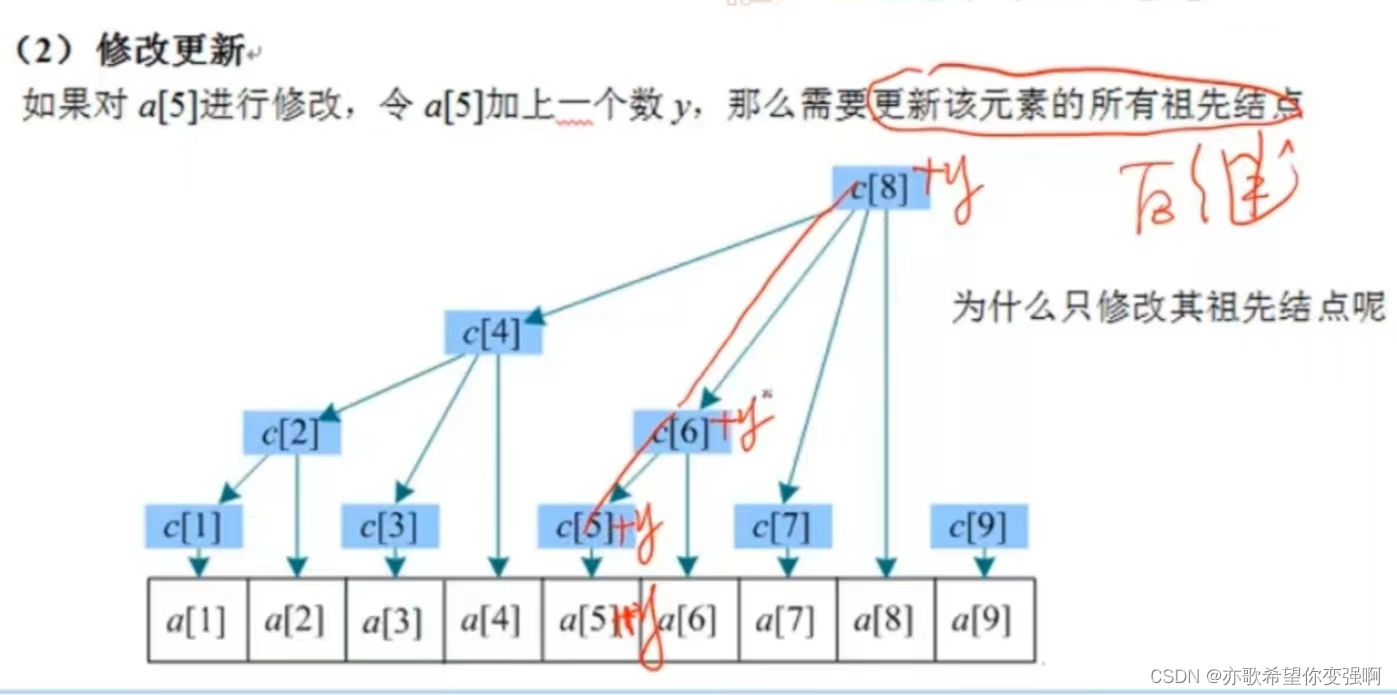
树状数组步骤:
单点修改更新add:找后继 更新该元素所有的祖先节点
查询前缀和sum:找前驱 加上左侧所有子树的根(也就是自己的前兄弟,故称为前驱)
#include <bits/stdc++.h>//一维树状数组 性能是log(n)
using namespace std;
typedef long long ll;
const int maxn=10000;
ll c[maxn];//c[]为树状数组
int n,a[maxn];
int lowbit(int i){ return (-i)&i;}
//获取c[i]区间的长度(计算机中的负数是以补码来存的)
void add(int i,int z){ for(;i<=n;i+=lowbit(i)) c[i]+=z;}
//c[i]的后继都加上z:直接后继为[i+lowbit(i)]
ll sum(int i){//求前缀和a[1]~a[i],把i前面所有的根加上即可:直接前驱为[i-lowbit(i)]ll s=0;for(;i>0;i-=lowbit(i)) s+=c[i];return s;
}ll sum(int i,int j){ return sum(j)-sum(i-1);}//求区间和int main(){cin>>n;for(int i=1;i<=n;i++){//数组必须从1开始输入cin>>a[i];add(i,a[i]);//点更新,更新树状数组} int x1,x2;cin>>x1;cout<<sum(x1)<<'\n';cin>>x1>>x2;cout<<sum(x1,x2);return 0;
}那么仅仅把sum改成从(1,1)到(x,y)求和即可变成二维的树状数组
#include <bits/stdc++.h>//二维树状数组
using namespace std;
typedef long long ll;
const int maxn=10000;
ll c[maxn][maxn];
int n,a[maxn][maxn];int lowbit(int i){ return (-i)&i;}void add(int x,int y,int z){for(int i=x;i<=n;i+=lowbit(i))for(int j=y;j<=n;j+=lowbit(j)){c[i][j]+=z;}
}ll sum(int x,int y){//求(1,1)到(x,y)和ll s=0;for(int i=x;i>0;i-=lowbit(i))for(int j=y;j>0;j-=lowbit(j)){s+=c[i][j];}return s;
}ll sum(int x1,int y1,int x2,int y2){return sum(x2,y2)-sum(x1-1,y2)-sum(x2,y1-1)+sum(x1-1,y1-1);
}int main(){cin>>n;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){cin>>a[i][j];add(i,j,a[i][j]);}int x1,y1,x2,y2;cin>>x1>>y1;cout<<sum(x1,y1)<<'\n';cin>>x1>>y1>>x2>>y2;cout<<sum(x1,y1,x2,y2);}
线段树点更新
线段树思想:建立一颗二叉树来用每个节点去维护对应区间的信息
线段树的本质是在4maxn大小的一维树形离散数组tree(节点)上存储区间的信息。建立,更新和查询也都是离散的
线段树操作是找到并修改叶节点信息来维护整棵树,查询是找所有的对应节点
要注意:
我们建立的二叉树在非叶子层时都是满二叉树。所以k节点的左孩子一定是2k,右孩子一定是2k+1另外k(节点)的值和l,r的值没有任何关系,只不过是l==r时候k是叶子节点
下图是初始化线段树的节点号
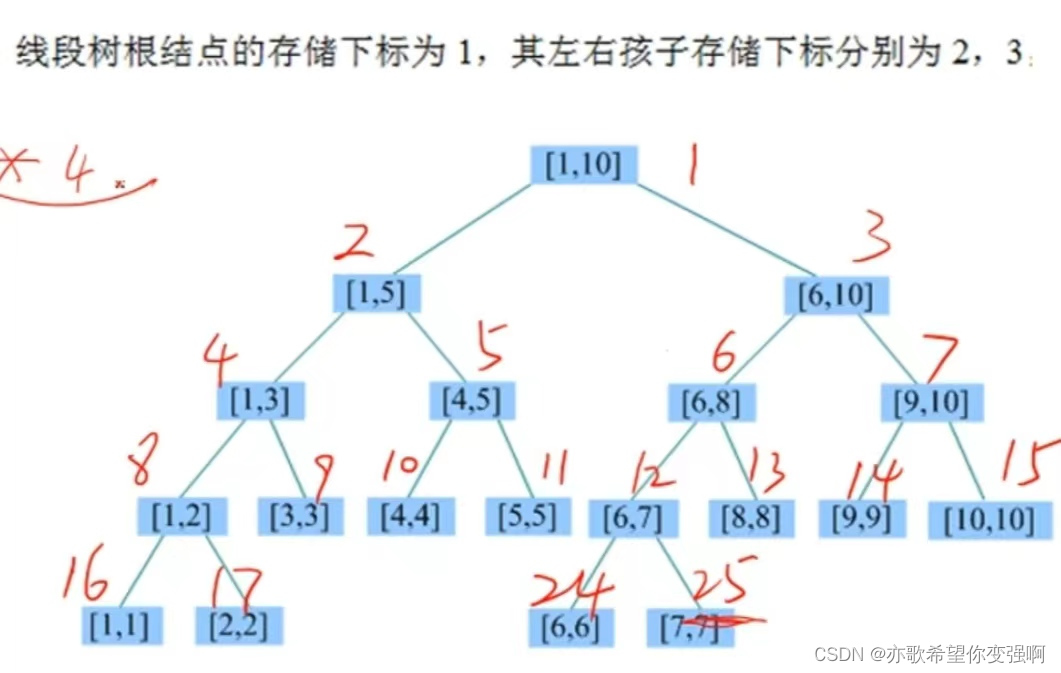
但是整棵树一定是按照dfs序来更新的,也因此叶子节点也是dfs序更新的
点更新步骤:
build:初始化节点信息:找到叶节点放置数组信息,然后上传到所有节点更新信息
update:找到对应的点将i下标的值更新为v
query: 找到对正确的节点就返回,否则就继续分叉找
千万别看代码多长,基本就函数中最前面的几句有用,剩余操作的都是在找孩子进行递归。
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005,INF=0x3f3f3f3f;
int n,a[maxn];
struct node{ int l,r,mx;}tree[maxn*4];//存放左右端点l,r,mx为区间最值,tree存放树节点号void build(int k,int l,int r){//创建线段树:初始化每个节点tree[k].l=l;tree[k].r=r;if(l==r){tree[k].mx=a[l];return ;}int mid=(l+r)/2;build(k<<1,l,mid);//建树时候范围一定要变化build(k<<1|1,mid+1,r);tree[k].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//创建完成孩子后再更新最大值
}void update(int k,int i,int v){//单点修改:在k节点将i下标的值更新为vif(tree[k].l==tree[k].r&&tree[k].l==i){//找i下标的叶子更新tree[k].mx=v;return ;}int mid=(tree[k].l+tree[k].r)/2;if(i<=mid) update(k<<1,i,v);//否则就进入左子树lc或右子树更新rcelse update(k<<1|1,i,v);tree[k].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//孩子更新完后修改最大值
}int query(int k,int l,int r){//区间查询:找到对正确的节点就返回,否则就继续分叉找if(tree[k].l>=l&&tree[k].r<=r){return tree[k].mx;//找到了}int mid=(tree[k].l+tree[k].r)/2;int maxx=-INF;if(l<=mid){//否则就找左子树或右子树的最值maxx=max(maxx,query(k<<1,l,r));}if(r>mid){maxx=max(maxx,query(k<<1|1,l,r));}return maxx;
}void print(int k){if(tree[k].mx){cout<<k<<"\t"<<tree[k].l<<"\t"<<tree[k].r<<"\t"<<tree[k].mx<<"\t"<<'\n';print(k<<1);print((k<<1)+1);}
}int main(){int l,r,i,v;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];build(1,1,n);//创建二叉线段树,为啥传入树根呢?答:方便找左右孩子print(1);cin>>l>>r;cout<<query(1,l,r)<<'\n';//查询区间最值cin>>i>>v;update(1,i,v);//点更新print(1);cin>>l>>r;cout<<query(1,l,r)<<'\n';
}输入样例后建立的二叉树:
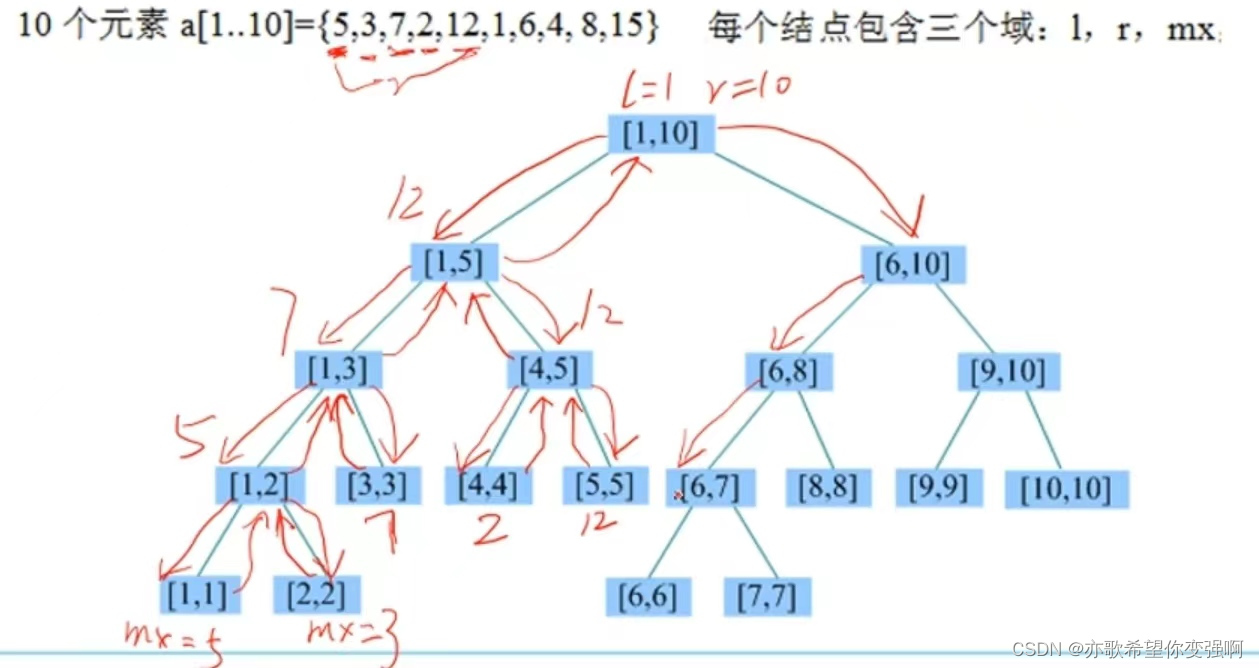
线段树区间更新
区间更新步骤:
创建线段树:初始化节点信息:找到叶节点放置数组信息,然后上传到所有节点更新信息
区间修改:在k节点上修改[l,r]区间为v值,整体包含就做懒标,否则就继续分叉(分叉前一定要懒标下移)
区间查询:找到对正确的节点就返回,否则就继续分叉找(分叉前一定要懒标下移)
也就是相对点更新来讲多了懒标的处理
#include <bits/stdc++.h>
using namespace std;
const int maxn=100005,INF=0x3f3f3f3f;
int n,a[maxn];
struct node{ int l,r,mx,lz;}tree[maxn*4];//存放左右端点l,r,mx表示区间[l,r]最值,lz表示懒标 tree存放树节点号
//二叉树的本质是在4k的一维dfs序的树形离散数组(节点)上存储的信息。另外k(节点)的值和l,r的值没有任何关系,只不过是l==r时候k是叶子节点
void lazy(int k,int v){tree[k].mx=tree[k].lz=v;}//给节点k打懒标void pushdown(int k){//从k节点下传懒标(传给子树),只会传一次,否则就退化成单点修改了lazy(k<<1,tree[k].lz);lazy(k<<1|1,tree[k].lz);//+的优先级太高了tree[k].lz=-1;//清除当前节点懒标
}void build(int k,int l,int r){//创建线段树:创建二叉树,然后在叶节点放置数组信息,然后上传到所有节点更新信息tree[k].l=l;tree[k].r=r;tree[k].lz=-1;//初始化节点if(l==r){tree[k].mx=a[l];return ;//按dfs顺序更新叶子}int mid=(l+r)/2;build(k<<1,l,mid);//建树时候范围一定要变化build(k<<1|1,mid+1,r);//左右孩子节点为2k和2k+1,分别维护[l,mid]和[mid+1,r]的区间信息tree[k].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//更新最大值
}void update(int k,int l,int r,int v){//区间修改:在k节点上修改[l,r]区间为v值,整体包含就做懒标,否则就继续分叉if(tree[k].l>=l&&tree[k].r<=r){//恰好找到区间(覆盖也行)return lazy(k,v);//直接做懒标记并结束本层,这个return不是返回值的}if(tree[k].lz!=-1) pushdown(k);//有懒标,先下移再进入子树(这样下个节点的lz和mx就更新了)int mid=(tree[k].l+tree[k].r)/2;if(l<=mid) update(k<<1,l,r,v);//传节点即可,因为我们用的是节点的信息(build时是l到mid区间为左子树,所以必须l<=mid)if(r>mid) update(k<<1|1,l,r,v);tree[k].mx=max(tree[k<<1].mx,tree[k<<1|1].mx);//更新最大值
}int query(int k,int l,int r){//区间查询:找到对正确的节点就返回,否则就继续分叉找if(tree[k].l>=l&&tree[k].r<=r){//找到就返回return tree[k].mx;}if(tree[k].lz!=-1) pushdown(k);//有懒标,先下移再进入子树int mid =(tree[k].l+tree[k].r)/2;int maxx=-INF;if(l<=mid) maxx=max(maxx,query(k<<1,l,r));//否则就找左子树或右子树的最值if(r>mid) maxx=max(maxx,query(k<<1|1,l,r));return maxx;
}void print(int k){if(tree[k].mx){//从根开始dfs顺序访问每个节点(1,2,3 ……)cout<<k<<"\t"<<tree[k].l<<"\t"<<tree[k].r<<"\t"<<tree[k].mx<<"\t"<<'\n';print(k<<1);print(k<<1|1);}
}int main(){int l,r,v;cin>>n;for(int i=1;i<=n;i++) cin>>a[i];build(1,1,n);//创建线段树 print(1);cin>>l>>r;cout<<query(1,l,r)<<'\n';//区间查询cin>>l>>r>>v;update(1,l,r,v);//区间修改print(1);for(int i=1;i<=n;i++)cout<<a[i]<<' ';cout<<"\n";while(l){cin>>l>>r;cout<<query(1,l,r)<<'\n';}
}