本章节是单节点走向分布式节点的一个重要部分。
- 一致性哈希(consistent hashing)的原理以及为什么要使用一致性哈希。
- 实现一致性哈希代码,添加相应的测试用例
1.多节点部署遇到的问题
上一章节完成了一个单节点的缓存服务器。那对于一个单节点来说,读写缓存都是针对同一个节点的,那应该是不会出错的。
该对哪个节点进行访问?
而当我们的缓存服务器节点变多后,需要访问那个节点,需要写缓存到哪个节点?
比如:我们插入一条缓存数据groupName=scores,key=tom时,可以随机找一个结点A来插入,但当想要访问该缓存数据时候,我们要怎样才能定位到节点A?
这就引出了哈希算法。
比如当前有10个节点,给每个节点进行编号,0,1,2,3....9。对存入的key进行hash运算再%10,拿到一个值,假如是2,那就把该数据存储到编号是2的节点上。而当需要方位该key时候,也进行hash运算再%10,就可以得到编号是2,就去访问编号为2的结点即可。
哈希算法的缺陷--分布式节点数量变更
简单求取 Hash 值解决了缓存性能的问题,但是没有考虑节点数量变化的场景。假设,移除了其中一台节点,只剩下 9 个,那么之前 hash(key) % 10 变成了 hash(key) % 9,也就意味着几乎缓存值对应的节点都发生了改变。即几乎所有的缓存值都失效了。节点在接收到对应的请求时,均需要重新去数据源获取数据,容易出大问题。
这时候,就要出动一致性哈希算法。
2.一致性哈希算法
一致性哈希是将整个哈希值空间组织成一个虚拟的圆环。其将 key 映射到 2^32 的空间中,将这个数字首尾相连,形成一个环。整个空间按顺时针方向组织,0和2^32-1在零点中方向重合。
该算法的两个步骤:
- 把服务器按照IP或主机名作为关键字进行哈希,这样就能确定其在哈希环的位置。
- 然后计算 key 的哈希值,放置在环上,顺时针寻找到的第一个节点,就是应选取的节点/机器。
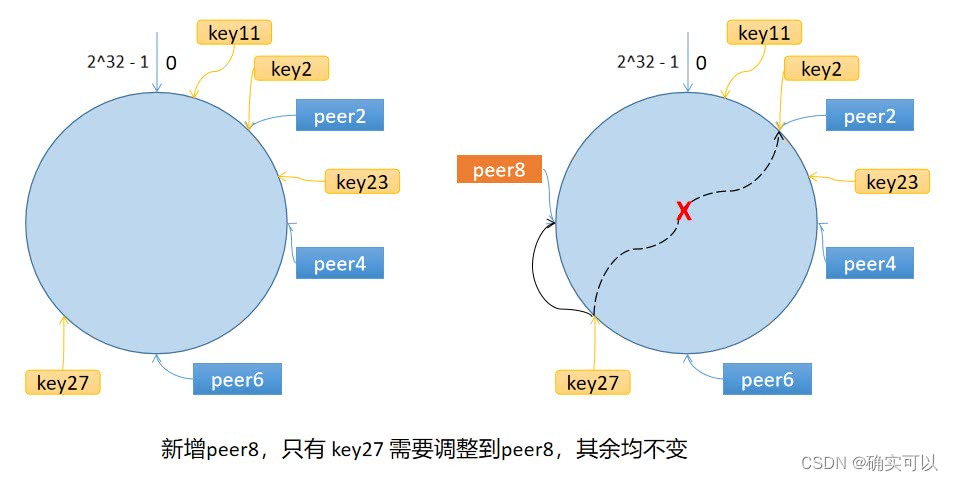 图片来自极客兔兔
图片来自极客兔兔
环上有 peer2,peer4,peer6 三个节点,按照顺时针,key11,key2,key27 均映射到 peer2,key23 映射到 peer4。
节点数量减少或扩张的情况分析
如果新增节点 peer8,假设它新增位置如图所示,那么只有 key27 从 peer2 调整到 peer8,其余的映射均没有发生改变。
也就是说,一致性哈希算法,在新增/删除节点时,只需要重新定位该节点附近的一小部分数据,而不需要重新定位所有的节点,具有较好的容错性和可扩展性,可以较好解决分布式节点数量的变更问题。
数据倾斜问题,可用虚拟节点
如果节点较少容易出现节点分布不均衡造成数据倾斜问题。例如下图左边中的 节点1和节点2的例子。大部分的 key 都会被分配给 节点2,key 过度向 节点2 倾斜,缓存节点间负载不均。
为了解决数据存储不平衡的问题,一致性哈希算法引入了虚拟节点机制,即对每个节点计算多个哈希值,每个计算结果位置都放置在对应节点中,这些节点称为虚拟节点。
具体做法可以在服务器IP或主机名的后面增加编号来实现,例如下图的情况,一共两个节点,缓存节点间负载不均。可以为每个服务节点增加三个虚拟节点,于是可以分为节点1#A、节点1#B、节点1#B,具体位置如下图所示:
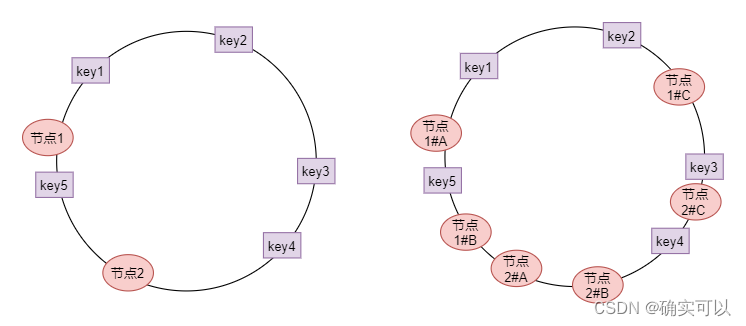
具体的步骤:
- 第一步,计算虚拟节点的 Hash 值,放置在环上。
- 第二步,计算 key 的 Hash 值,在环上顺时针寻找到应选取的虚拟节点,例如是 节点2#B,那么就对应真实的节点2。
虚拟节点扩充了节点的数量,解决了节点较少的情况下数据容易倾斜的问题。而且代价很小,只需要增加一个字典(map)维护真实节点与虚拟节点的映射关系即可。
3.一致性哈希代码实现
type HashFunc func(data []byte) uint32// 定义哈希环
type HashRing struct {hashFunc HashFunc //定义的哈希算法replicas int //虚拟节点的数量keys []int //排序好的哈希环hashMap map[int]string //虚拟节点与真实节点的映射关系,key是虚拟节点的哈希值,value是真实节点名称
}func NewHash(replicas int, fn HashFunc) *HashRing {h := &HashRing{replicas: replicas,hashFunc: fn,hashMap: make(map[int]string),}if h.hashFunc == nil {h.hashFunc = crc32.ChecksumIEEE}return h
}- 定义了函数类型
HashRing,采取依赖注入的方式,允许用于替换成自定义的 Hash 函数,也方便测试时替换,默认为crc32.ChecksumIEEE算法。 Map是一致性哈希算法的主数据结构,包含 4 个成员变量:Hash 函数hashFunc;虚拟节点倍数replicas;哈希环keys;虚拟节点与真实节点的映射表hashMap,键是虚拟节点的哈希值,值是真实节点的名称。
添加真实节点/机器的 Add() 方法
func (h *HashRing) Add(realNodeName ...string) {for _, name := range realNodeName {for i := 0; i < h.replicas; i++ {hash := int(h.hashFunc([]byte(strconv.Itoa(i) + name)))h.keys = append(h.keys, hash)h.hashMap[hash] = name}}sort.Ints(h.keys)
}Add函数允许传入 0 或 多个真实节点的名称。- 对每一个真实节点 name,对应创建 h
.replicas个虚拟节点,虚拟节点的名称是:strconv.Itoa(i) +name,即通过添加编号的方式区分不同虚拟节点。比如当前i是1,name是"2",那其编号就是"12"。 - 使用 h
.hash()计算虚拟节点的哈希值,之后添加到环h.keys上。 - 在
hashMap中增加虚拟节点和真实节点的映射关系。 - 最后一步,环上的哈希值排序。
选择节点的 Get() 方法
// 选择节点
func (h *HashRing) Get(key string) string {if len(h.keys) == 0 {return ""}hash := int(h.hashFunc([]byte(key)))idx := sort.Search(len(h.keys), func(i int) bool {return h.keys[i] >= hash})return h.hashMap[h.keys[idx%len(h.keys)]]
}- 第一,计算 key 的哈希值。
- 第二步,顺时针找到第一个匹配的虚拟节点的下标
idx,从 h.keys 中获取到对应的哈希值。如果idx == len(m.keys),说明应选择m.keys[0],因为m.keys是一个环状结构,所以用取余数的方式来处理这种情况。 - 第三步,通过
hashMap映射得到真实的节点。
4. 测试
在consistenthash_test.go文件中。
如果要进行测试,那么我们需要明确地知道每一个传入的 key 的哈希值,那使用默认的 crc32.ChecksumIEEE 算法显然达不到目的。所以在这里使用了自定义的 Hash 算法。自定义的 Hash 算法只处理数字,传入字符串表示的数字,返回对应的数字即可。
func TestHashing(t *testing.T) {//创建哈希环,每个真实节点有三个虚拟节点hash := NewHash(2, func(key []byte) uint32 {i, _ := strconv.Atoi(string(key))return uint32(i)})//添加3个真实节点,哈希函数后,//"2"对应的虚拟节点是2/12/22,4的是/4/14/24hash.Add("2", "4")//map的key是缓存数据key,value是真实节点testCases := map[string]string{"4": "4","11": "2","16": "2","27": "2",}for k, v := range testCases {if hash.Get(k) != v {t.Errorf("Asking for %s, should have yielded %s", k, v)}}//添加真实节点"8",其对应的虚拟节点是8/18hash.Add("8")testCases["16"] = "8"for k, v := range testCases {if hash.Get(k) != v {t.Errorf("Asking for %s, should have yielded %s", k, v)}}
}测试代码中对应的哈希环如图
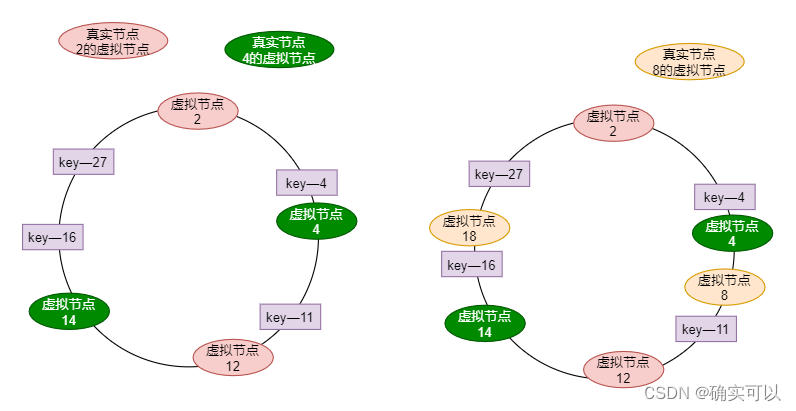
添加了真实节点"2","4"后,虚拟节点如图左边所示,要访问的key经过哈希运算后,为了简单就还是原来的值,那key的分布也就如图左边所示啦。
测试用例就是通过key去找到真实的节点。在添加真实节点"8"前,key为4对应的虚拟节点是4,那真实节点是4,依次类推,可自行测试。
完整代码:https://github.com/liwook/Go-projects/tree/main/go-cache/4-consistent-hash