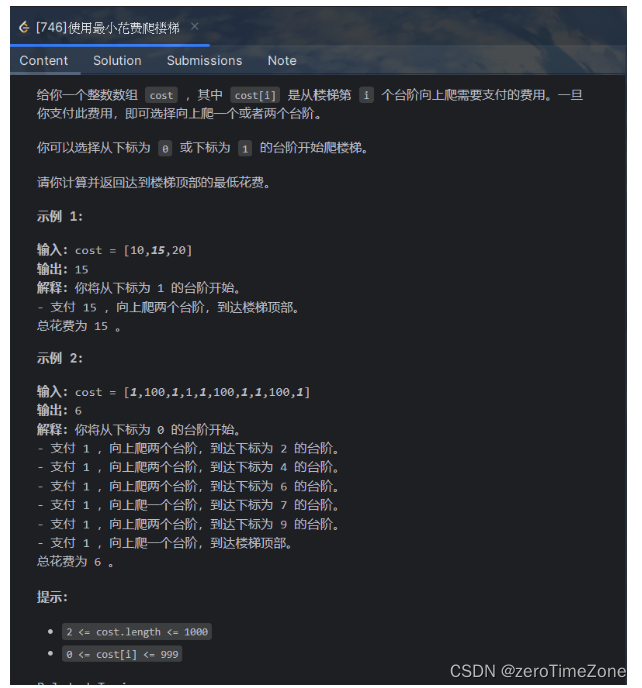
//给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。 
//
// 你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。 
//
// 请你计算并返回达到楼梯顶部的最低花费。 
//
// 
//
// 示例 1： 
//
// 
//输入：cost = [10,15,20]
//输出：15
//解释：你将从下标为 1 的台阶开始。
//- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
//总花费为 15 。
// 
//
// 示例 2： 
//
// 
//输入：cost = [1,100,1,1,1,100,1,1,100,1]
//输出：6
//解释：你将从下标为 0 的台阶开始。
//- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
//- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
//- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
//- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
//- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
//- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
//总花费为 6 。
// 
//
// 
//
// 提示： 
//
// 
// 2 <= cost.length <= 1000 
// 0 <= cost[i] <= 999 
// 
//
// Related Topics 数组 动态规划 👍 1382 👎 0//leetcode submit region begin(Prohibit modification and deletion)
class Solution {/*** 给出一个数组为cost[]，它长度为n，那么它可达到数组length + 1层或length + 2层；* 这个终点具体指什么说得很明白，由示例可知，爬楼梯的终点就是指length + 1层即为终点** @param cost* @return*/public int minCostClimbingStairs(int[] cost) {//到达第0层的台阶因不需要动因而耗费0int fn2 = 0;//到达第1层的台阶，因为可以选择直接从第1阶开始，因而这种方式到达第1阶，是不耗费的int fn1 = 0;//到达第n层所需的最小耗费；n最大为leng + 1，即此次爬楼梯的终点目标层数int fn = 0;//下标为cost[i]的花费，指的是从第（i + 1）层向上爬所需的耗费for (int n = 2; n < cost.length + 1; n++) {fn = Math.min(fn2 + cost[n - 2], fn1 + cost[n - 1]);fn2 = fn1;fn1 = fn;}return fn;}
}
//leetcode submit region end(Prohibit modification and deletion)