第4章 深度学习的数学基础
目录
4.1 向量
4.2 求和符号
4.3 累乘符号
4.4 导数
4.5 偏导数
4.6 矩阵
4.7 指数函数和对数函数
注意:4.6和4.7位于4.2章
第4章 深度学习的数学基础
本章总结一下机器学习所需的数学知识,同时介绍如何在Python中使用这些知识。
4.1 向量
4.1.1 什么是向量
向量由几个数横向或纵向排列而成。
数纵向排列的向量叫作列向量,如下式4-1所示的变量就是列向量:
a = [ 1 3 ] , b = [ 2 1 ] (4-1) \boldsymbol{a}=\left[\begin{array}{l} 1 \\ 3 \end{array}\right], \boldsymbol{b}=\left[\begin{array}{l} 2 \\ 1 \tag{4-1} \end{array}\right] a=[13],b=[21](4-1)
数横向排列的向量叫作行向量,如下式4-2所示的变量就是行向量:
c = [ 1 2 ] , d = [ 1 3 5 4 ] (4-2) \boldsymbol{c}=\left[\begin{array}{ll} 1 & 2 \end{array}\right], \boldsymbol{d}=\left[\begin{array}{llll} 1 & 3 & 5 & 4 \tag{4-2} \end{array}\right] c=[12],d=[1354](4-2)
构成向量的一个一个数叫作元素。向量中的元素个数叫作向量的维度。如上例所示, a \boldsymbol a a为二维列向量, d \boldsymbol d d为四维行向量。如 a \boldsymbol a a和 b \boldsymbol b b所示,向量一般用小写粗斜体表示。
与向量不同的普通的单个数叫作标量。标量一般用小写斜体表示为如 a 、 b a、b a、b。
向量右上角的 T T T是转置符号,表示将列向量转换为行向量,或者将行向量转换为列向量,如下式4-3所示:
a T = [ 1 3 ] T = [ 1 3 ] , d T = [ 1 3 5 4 ] T = [ 1 3 5 4 ] (4-3) \boldsymbol{a}^{\mathrm{T}}=\left[\begin{array}{l} 1 \\ 3 \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ll} 1 & 3 \end{array}\right], \boldsymbol{d}^{\mathrm{T}}=\left[\begin{array}{llll} 1 & 3 & 5 & 4 \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{l} 1 \\ 3 \\ 5 \\ 4 \tag{4-3} \end{array}\right] aT=[13]T=[13],dT=[1354]T= 1354 (4-3)
机器学习类教材中,除了从数学上来说必须使用转置符号的情况外,考虑到行距,有时也会把
a = [ 1 3 ] a=\left[\begin{array}{l} 1 \\ 3 \end{array}\right] a=[13]
写成 a = [ 1 3 ] T \boldsymbol{a}=\left[\begin{array}{ll} 1 & 3 \end{array}\right]^{\mathrm{T}} a=[13]T。
4.1.2 用Python定义向量
接下来,我们用Python定义向量。
要想使用向量,必须先使用import导入NumPy库。
# 代码清单 4-1-(1)
import numpy as np
然后,使用np.array定义向量a。
# 代码清单 4-1-(2)
a = np.array([2, 1])
print(a)
运行type,可以看到a的类型为numpy.ndarray。
# 代码清单 4-1-(3)
type(a)
运行结果:
numpy.ndarray
4.1.3 列向量的表示方法
事实上,一维的ndarray类型没有纵横之分,往往都表示为行向量。
不过用特殊形式的二维ndarray表示列向量也是可以的。
ndarray类型可以表示2×2的二维数组(矩阵),如代码所示。
# 代码清单 4-1-(4)
c = np.array([[1, 2], [3, 4]])
print(c)
输出结果:
[[1 2][3 4]]
用这个方式定义2×1的二维数组,就可以用它表示列向量。
# 代码清单 4-1-(5)
d = np.array([[1], [2]])
print(d)
输出结果:
[[1][2]]
向量通常定义为一维ndarray类型,必要时可以用二维ndarray类型。
4.1.4 转置的表示方法
使用“变量名.T”表示。
# 代码清单 4-1-(6)
print(d.T)
print(d)
print(d.T.T)
输出结果:
[[1 2]]
[[1][2]]
[[1][2]]
使用d.T.T循环两次转置操作之后,就会变回原来的d。
注意:转置操作对于二维ndarray类型有效,对于一维ndarray类型是无效的。
print(a)
print(a.T)
输出结果:
[2 1]
[2 1]
4.1.5 加法和减法
接下来,我们思考下面两个向量 a \boldsymbol{a} a和 b \boldsymbol{b} b:
a = [ 2 1 ] , b = [ 1 3 ] (4-4) \boldsymbol{a}=\left[\begin{array}{l} 2 \\ 1 \end{array}\right], \boldsymbol{b}=\left[\begin{array}{l} 1 \\ 3 \tag{4-4} \end{array}\right] a=[21],b=[13](4-4)
首先进行加法运算。向量的加法运算 a + b \boldsymbol{a}+\boldsymbol{b} a+b是将各个元素相加:
a + b = [ 2 1 ] + [ 1 3 ] = [ 2 + 1 1 + 3 ] = [ 3 4 ] (4-5) \boldsymbol{a}+\boldsymbol{b}=\left[\begin{array}{l} 2 \\ 1 \end{array}\right]+\left[\begin{array}{l} 1 \\ 3 \end{array}\right]=\left[\begin{array}{c} 2+1 \\ 1+3 \end{array}\right]=\left[\begin{array}{l} 3 \\ 4 \tag{4-5} \end{array}\right] a+b=[21]+[13]=[2+11+3]=[34](4-5)
向量的加法运算可以通过图形解释。首先,将向量的元素看作坐标点,将向量看作从坐标原点开始延伸到元素坐标点的箭头。这样的话,单纯地将各个元素相加的向量加法运算就可以看作,对以 a \boldsymbol{a} a和 b \boldsymbol{b} b为邻边的平行四边形求对角线(图4-1)。

图4-1 向量的加法运算
运行 a + b \boldsymbol{a}+\boldsymbol{b} a+b的加法运算之后,程序会返回预期的答案,可知 a \boldsymbol{a} a和 b \boldsymbol{b} b不是list类型,而是被当作向量处理的(对于list类型,加法运算的作用是连接)。
# 代码清单 4-1-(7)
a = np.array([2, 1])
b = np.array([1, 3])
la=list(a)
lb=list(b)
print(a + b)
print(la+lb)
输出结果:
[3 4]
[2, 1, 1, 3]
向量的减法运算与加法运算相同,是对各个元素进行减法运算:
a − b = [ 2 1 ] − [ 1 3 ] = [ 2 − 1 1 − 3 ] = [ 1 − 2 ] (4-6) a-b=\left[\begin{array}{l} 2 \\ 1 \end{array}\right]-\left[\begin{array}{l} 1 \\ 3 \end{array}\right]=\left[\begin{array}{c} 2-1 \\ 1-3 \end{array}\right]=\left[\begin{array}{c} 1 \\ -2 \tag{4-6} \end{array}\right] a−b=[21]−[13]=[2−11−3]=[1−2](4-6)
Python计算代码如下:
# 代码清单 4-1-(8)
a = np.array([2, 1])
b = np.array([1, 3])
print(a - b)
输出结果:
[ 1 -2]
那么,减法运算该怎么借助图形解释呢?
a − b \boldsymbol{a}-\boldsymbol{b} a−b就是 a + ( − b ) \boldsymbol{a}+\boldsymbol{(-b)} a+(−b),可以看作 a \boldsymbol{a} a和 − b \boldsymbol{-b} −b的加法运算。从图形上来说, − b \boldsymbol{-b} −b的箭头方向与 b \boldsymbol{b} b相反。所以, a + ( − b ) \boldsymbol{a}+\boldsymbol{(-b)} a+(−b)是以 a \boldsymbol{a} a和 − b \boldsymbol{-b} −b为邻边的平行四边形的对角线(图4-2)。
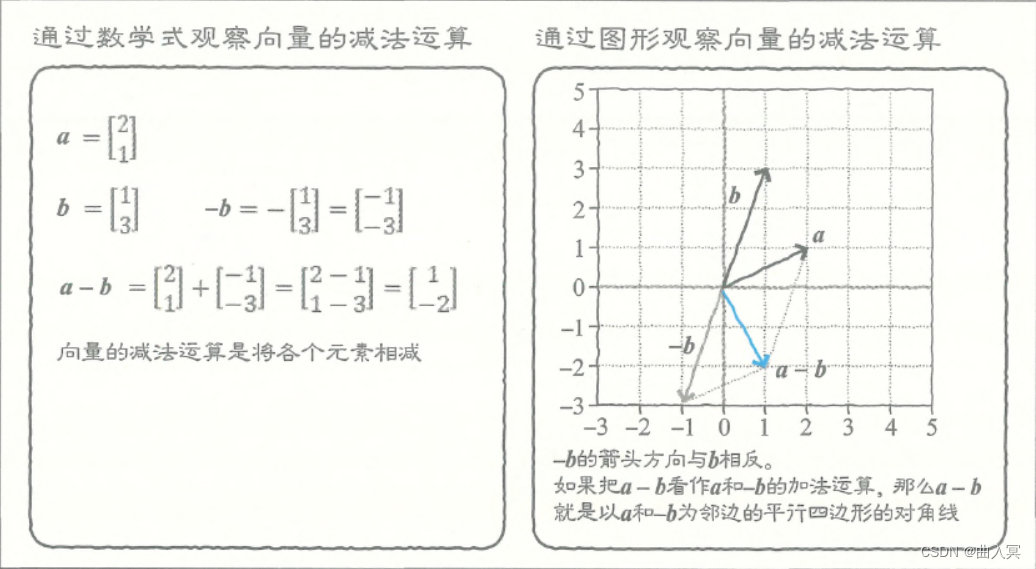
图4-2 向量的减法运算
4.1.6 标量积
在标量与向量的乘法运算中,标量的值会与向量的各个元素分别相乘,比如 2 a 2\boldsymbol{a} 2a:
2 a = 2 × [ 2 1 ] = [ 2 × 2 2 × 1 ] = [ 4 2 ] (4-7) 2 \boldsymbol{a}=2 \times\left[\begin{array}{l} 2 \\ 1 \end{array}\right]=\left[\begin{array}{l} 2 \times 2 \\ 2 \times 1 \end{array}\right]=\left[\begin{array}{l} 4 \\ 2 \tag{4-7} \end{array}\right] 2a=2×[21]=[2×22×1]=[42](4-7)
在Python中,式4-7的计算如代码如下:
# 代码清单 4-1-(9)
print(2 * a)
输出结果:
[4 2]
从图形上来说,向量的长度变成了标量倍(图4-3)。
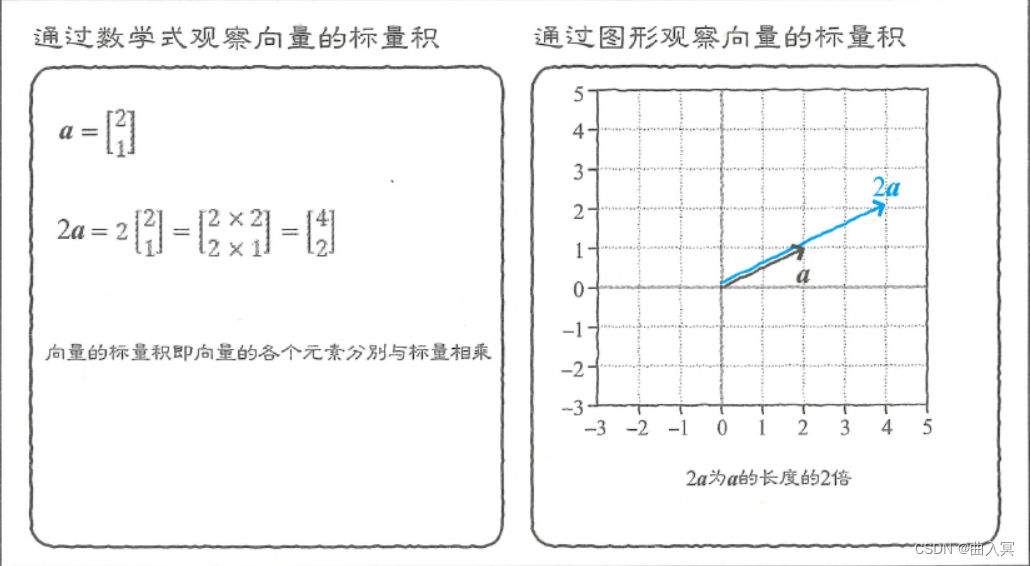
图4-3 向量的标量积
4.1.7 内积
向量与向量之间的乘法运算叫作内积。内积是由相同维度的两个向量进行的运算,通常用“ ⋅ \cdot ⋅”表示,这在机器学习涉及的数学中很常见。内积运算是把对应的元素相乘,然后求和,比如 b = [ 1 3 ] T 、 c = [ 4 2 ] T \boldsymbol{b}=\left[\begin{array}{ll} 1 & 3 \end{array}\right]^{\mathrm{T}}、\boldsymbol{c}=\left[\begin{array}{ll} 4 & 2 \end{array}\right]^{\mathrm{T}} b=[13]T、c=[42]T的内积:
b ⋅ c = [ 1 3 ] ⋅ [ 4 2 ] = 1 × 4 + 3 × 2 = 10 (4-8) \boldsymbol{b} \cdot \boldsymbol{c}=\left[\begin{array}{l} 1 \\ 3 \end{array}\right] \cdot\left[\begin{array}{l} 4 \\ 2 \tag{4-8} \end{array}\right]=1 \times 4+3 \times 2=10 b⋅c=[13]⋅[42]=1×4+3×2=10(4-8)
在Python中,我们使用“变量名1.dot(变量名2)”计算内积(代码清单4-1-(10))。
# 代码清单 4-1-(10)
b = np.array([1, 3])
c = np.array([4, 2])
print(b.dot(c))
print(b*c)
输出结果:
10
[4 6]
但是,内积表示的究竟是什么呢?如图4-4所示,设 b \boldsymbol{b} b在 c \boldsymbol{c} c上的投影向量为 b ′ \boldsymbol{b'} b′,那么 b ′ \boldsymbol{b'} b′和 c \boldsymbol{c} c的长度相乘即可得到内积的值。
当两个向量的方向大致相同时,内积的值较大。相反,当两个向量近乎垂直时,内积的值较小;当完全垂直时,内积的值为0。可以说,内积与两个向量的相似度相关。

图4-4 向量的内积
但是,请注意内积与向量自身的大小也相关。即使两个向量方向相同,只要其中一个向量变成原来的2倍,那么内积也会变成原来的2倍。
x = np.array([1,1])
y = np.array([-1,1])
print(x.dot(y))z = np.array([0,1])
print(x.dot(z))nz = np.array([-2,1])
print(x.dot(nz))
输出结果:
0
1
-1
4.1.8 向量的模
向量的模是指向量的长度,将向量夹在两个“ ∥ \| ∥”之间,即可表示向量的模。二维向量的模可计算为:
∥ a ∥ = ∥ [ a 0 a 1 ] ∥ = a 0 2 + a 1 2 (4-9) \|\boldsymbol{a}\|=\left\|\left[\begin{array}{c} a_{0} \\ a_{1} \tag{4-9} \end{array}\right]\right\|=\sqrt{a_{0}^{2}+a_{1}^{2}} ∥a∥= [a0a1] =a02+a12(4-9)
三维向量的模可计算为:
∥ a ∥ = ∥ [ a 0 a 1 a 2 ] ∥ = a 0 2 + a 1 2 + a 2 2 (4-10) \|\boldsymbol{a}\|=\left\|\left[\begin{array}{c} a_{0} \\ a_{1} \\ a_{2} \tag{4-10} \end{array}\right]\right\|=\sqrt{a_{0}^{2}+a_{1}^{2}+a_{2}^{2}} ∥a∥= a0a1a2 =a02+a12+a22(4-10)
在一般情况下,D维向量的模计算为:
∥ a ∥ = ∥ [ a 0 a 1 ⋯ a D − 1 ] ∥ = a 0 2 + a 1 2 + ⋯ + a D − 1 2 (4-11) \|\boldsymbol{a}\|=\left\|\left[\begin{array}{c} a_{0} \\ a_{1} \\ \cdots \\ a_{D-1} \tag{4-11} \end{array}\right]\right\|=\sqrt{a_{0}^{2}+a_{1}^{2}+\cdots+a_{D-1}^{2}} ∥a∥= a0a1⋯aD−1 =a02+a12+⋯+aD−12(4-11)
在Python中,我们使用np.linalg.norm()求向量的模。
# 代码清单 4-1-(11)
a = np.array([3, 4])
print(np.linalg.norm(a))
输出结果:
5.0
4.2 求和符号
求和符号 Σ \Sigma Σ(西格玛)会经常出现在机器学习教材中,比如,下式4-12的意思是“将从1到5的变量n的值全部相加”。
∑ n = 1 5 n = 1 + 2 + 3 + 4 + 5 (4-12) \sum_{n=1}^{5} n=1+2+3+4+5 \tag{4-12} n=1∑5n=1+2+3+4+5(4-12)
n n n用于简洁地表示长度较长的加法运算。对上式加以扩展,如式4-13所示,它表示“对于 Σ \Sigma Σ右边的 f ( n ) f(n) f(n),令变量 n n n的取值从 a a a开始递增1,直到 a a a变为 b b b,然后把所有 f ( n ) f(n) f(n)相加”。
∑ n = a b f ( n ) = f ( a ) + f ( a + 1 ) + ⋯ + f ( b ) (4-13) \sum_{n=a}^{b} f(n)=f(a)+f(a+1)+\cdots+f(b) \tag{4-13} n=a∑bf(n)=f(a)+f(a+1)+⋯+f(b)(4-13)
比如,令 f ( n ) = n 2 f(n)=n^2 f(n)=n2,则结果如式4-14所示。这跟编程中的for语句很像。
∑ n = 2 5 n 2 = 2 2 + 3 2 + 4 2 + 5 2 (4-14) \sum_{n=2}^{5} n^{2}=2^{2}+3^{2}+4^{2}+5^{2} \tag{4-14} n=2∑5n2=22+32+42+52(4-14)
4.2.1 带求和符号的数学式的变形
在思考机器学习的问题时,我们常常需要对带求和符号的数学式进行变形。接下来,思考一下如何变形。最简单的情况是求和符号右侧的函数 f ( n ) f(n) f(n)中没有 n n n,比如 f ( n ) = 3 f(n)=3 f(n)=3。这时,只需用相加的次数乘以 f ( n ) f(n) f(n)即可,所以可以去掉求和符号:
∑ n = 1 5 3 = 3 + 3 + 3 + 3 + 3 = 3 × 5 = 15 (4-15) \sum_{n=1}^{5} 3=3+3+3+3+3=3 \times 5=15 \tag{4-15} n=1∑53=3+3+3+3+3=3×5=15(4-15)
当 f ( n ) f(n) f(n)为“标量×2的函数”时,可以将标量提取到求和符号的外侧(左侧):
∑ n = 1 3 2 n 2 = 2 × 1 2 + 2 × 2 2 + 2 × 3 2 = 2 ( 1 2 + 2 2 + 3 2 ) = 2 ∑ n = 1 3 n 2 (4-16) \sum_{n=1}^{3} 2 n^{2}=2 \times 1^{2}+2 \times 2^{2}+2 \times 3^{2}=2\left(1^{2}+2^{2}+3^{2}\right)=2 \sum_{n=1}^{3} n^{2} \tag{4-16} n=1∑32n2=2×12+2×22+2×32=2(12+22+32)=2n=1∑3n2(4-16)
当求和符号作用于多项式时,可以将求和符号分配给各个项:
∑ n = 1 5 [ 2 n 2 + 3 n + 4 ] = 2 ∑ n = 1 5 n 2 + 3 ∑ n = 1 5 n + 4 × 5 (4-17) \sum_{n=1}^{5}\left[2 n^{2}+3 n+4\right]=2 \sum_{n=1}^{5} n^{2}+3 \sum_{n=1}^{5} n+4 \times 5 \tag{4-17} n=1∑5[2n2+3n+4]=2n=1∑5n2+3n=1∑5n+4×5(4-17)
之所以可以这样做,是因为无论是多项式相加,还是各项单独相加再求和,答案都是一样的。
4.1.7节的向量的内积也可以使用求和符号表示。比如 w = [ w 0 , w 1 ⋯ w D − 1 ] T \boldsymbol{w}=\left[w_{0},w_{1} \cdots w_{D-1}\right]^{\mathrm{T}} w=[w0,w1⋯wD−1]T和 x = [ x 0 , x 1 ⋯ x D − 1 ] T \boldsymbol{x}=\left[x_{0},x_{1} \cdots x_{D-1}\right]^{\mathrm{T}} x=[x0,x1⋯xD−1]T的内积可以使用“ ⋅ \cdot ⋅”表示为(图4-6):
w ⋅ x = w 0 x 0 + w 1 x 1 + ⋯ + w D − 1 x D − 1 = ∑ i = 0 D − 1 w i x i (4-18) \boldsymbol{w} \cdot \boldsymbol{x}=w_{0} x_{0}+w_{1} x_{1}+\cdots+w_{D-1} x_{D-1}=\sum_{i=0}^{D-1} w_{i} x_{i} \tag{4-18} w⋅x=w0x0+w1x1+⋯+wD−1xD−1=i=0∑D−1wixi(4-18)

图4-5矩阵表示法和元素表示法
图4-5左侧称为矩阵表示法(向量表示法),右侧称为元素表示法,而式4-18则可以看作在两者之间来回切换的一个式子。
4.2.2 通过内积求和
Σ \Sigma Σ跟编程中的for语句很像,根据式4-18, Σ \Sigma Σ也与内积有关,所以也可以通过内积计算 Σ \Sigma Σ。例如,从1加到1000的和为:
1 + 2 + ⋯ + 1000 = [ 1 1 ⋮ 1 ] ⋅ [ 1 2 ⋮ 1000 ] (4-19) 1+2+\cdots+1000=\left[\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right] \cdot\left[\begin{array}{c} 1 \\ 2 \\ \vdots \\ 1000 \tag{4-19} \end{array}\right] 1+2+⋯+1000= 11⋮1 ⋅ 12⋮1000 (4-19)
在Python中,式4-19的计算如代码如下所示。与for语句相比,这种方法的运算处理速度更快。
# 代码清单 4-2-(1)
import numpy as npa = np.ones(1000) # [1 1 1 ... 1]
b = np.arange(1,1001) # [1 2 3 ... 1000]
print(a.dot(b))
输出结果:
500500.0
4.3 累乘符号
累乘符号 Π \Pi Π与 Σ \Sigma Σ符号在使用方法上类似。 Π \Pi Π用于使 f ( n ) f(n) f(n)的所有元素相乘(图4-7):
∏ n = a b f ( n ) = f ( a ) × f ( a + 1 ) × ⋯ × f ( b ) (4-20) \prod_{n=a}^{b} f(n)=f(a) \times f(a+1) \times \cdots \times f(b) \tag{4-20} n=a∏bf(n)=f(a)×f(a+1)×⋯×f(b)(4-20)
下式是一个最简单的例子:
∏ n = 1 5 n = 1 × 2 × 3 × 4 × 5 (4-21) \prod_{n=1}^{5} n=1 \times 2 \times 3 \times 4 \times 5 \tag{4-21} n=1∏5n=1×2×3×4×5(4-21)
下式是累乘符号 Π \Pi Π作用于多项式的示例:
∏ n = 2 5 ( 2 n + 1 ) = ( 2 ⋅ 2 + 1 ) ( 2 ⋅ 3 + 1 ) ( 2 ⋅ 4 + 1 ) ( 2 ⋅ 5 + 1 ) (4-22) \prod_{n=2}^{5}(2 n+1)=(2 \cdot 2+1)(2 \cdot 3+1)(2 \cdot 4+1)(2 \cdot 5+1) \tag{4-22} n=2∏5(2n+1)=(2⋅2+1)(2⋅3+1)(2⋅4+1)(2⋅5+1)(4-22)
4.4 导数
大部分情况下,机器学习的问题可以归结为求函数取最小值(或最大值)时的输入的问题(最值问题)。因为函数具有在取最小值的地方斜率为0的性质,所以在求解这样的问题时,获取函数的斜率就变得尤为重要。推导函数斜率的方法就是求导。
4.4.1 多项式的导数
首先,我们以二次函数为例思考一下(图4-6左):
f ( w ) = w 2 (4-23) f(w)=w^2 \tag{4-23} f(w)=w2(4-23)
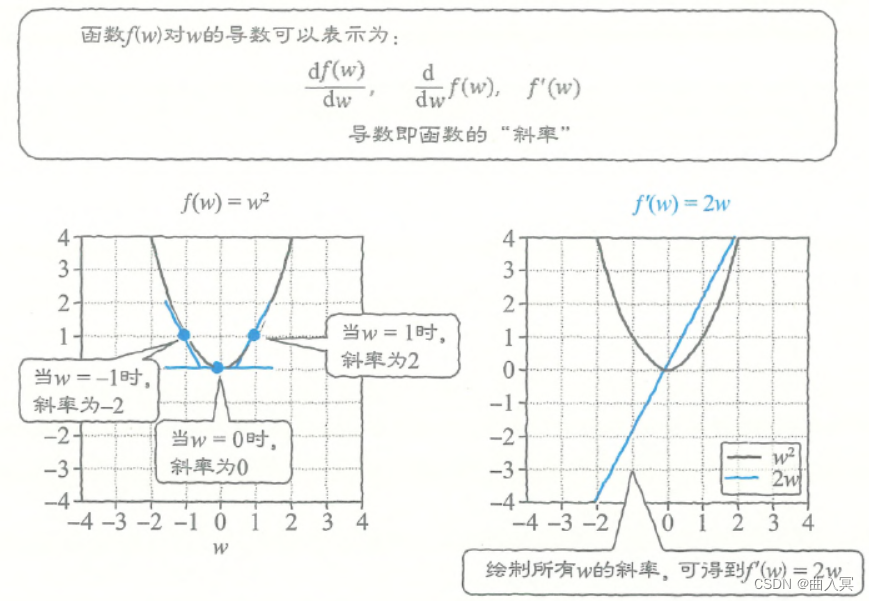
图4-6左 函数的导数表示斜率
import matplotlib.pyplot as plt #导入matplotlib库
import numpy as np #导入numpy库
import mpl_toolkits.axisartist as axisartist #并引入axisartist工具
%matplotlib inline#创建画布
fig = plt.figure(figsize=(8, 8))
#使用axisartist.Subplot方法创建一个绘图区对象ax
ax = axisartist.Subplot(fig, 111)
#将绘图区对象添加到画布中
fig.add_axes(ax)
#通过set_visible方法设置绘图区所有坐标轴隐藏
ax.axis[:].set_visible(False)
#ax.new_floating_axis代表添加新的坐标轴
ax.axis["x"] = ax.new_floating_axis(0,0)
#给x坐标轴加上箭头
ax.axis["x"].set_axisline_style("->", size = 1.0)
#添加y坐标轴,且加上箭头
ax.axis["y"] = ax.new_floating_axis(1,0)
ax.axis["y"].set_axisline_style("-|>", size = 1.0)
#设置x、y轴上刻度显示方向
ax.axis["x"].set_axis_direction("top")
ax.axis["y"].set_axis_direction("right")#生成x步长为0.05的列表数据
x = np.linspace(-5,5,200)
y=x**2
#设置x、y坐标轴的范围
plt.xlim(-5,5)
plt.ylim(-5, 25)
#绘制图形
plt.plot(x,y, c='violet')
plt.plot(x,-1-2*x,c='r')
plt.plot(x,2*x-1,c='g')
plt.plot(x,2*x,c='b')
输出结果:
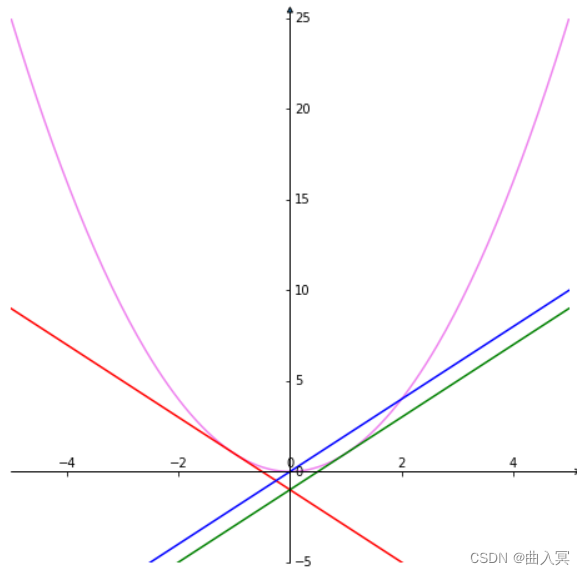
函数 f ( w ) f(w) f(w)对 w w w的导数可以有如下多种表示形式:
d f ( w ) d w , d d w f ( w ) , f ′ ( w ) (4-24) \frac{\mathrm{d} f(w)}{\mathrm{d} w}, \frac{\mathrm{d}}{\mathrm{d} w} f(w), f^{\prime}(w) \tag{4-24} dwdf(w),dwdf(w),f′(w)(4-24)
导数表示函数的斜率(上图右)。由于当 w w w发生变化时,函数的斜率也会随之发生变化,所以函数的斜率也是一个关于 w w w的函数。这个二次函数就是:
d d w w 2 = 2 w (4-25) \frac{\mathrm{d}}{\mathrm{d} w}w^2=2w \tag{4-25} dwdw2=2w(4-25)
在一般的情况下,我们可以使用下式简单求出 w n w^n wn形式的函数的导数:
d d w w n = n w n − 1 (4-26) \frac{\mathrm{d}}{\mathrm{d} w} w^{n}=n w^{n-1} \tag{4-26} dwdwn=nwn−1(4-26)
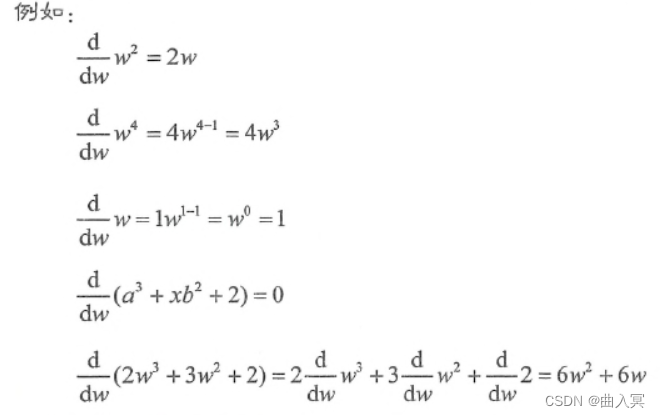
图4-7 幂函数的导数公式
比如,四次函数的导数为:
d d w w 4 = 4 w 4 − 1 = 4 w 3 (4-27) \frac{\mathrm{d}}{\mathrm{d} w} w^{4}=4 w^{4-1}=4 w^{3} \tag{4-27} dwdw4=4w4−1=4w3(4-27)
如果是一次函数,则导数如下式所示。不过,由于一次函数是直线,所以无论 w w w取值如何,斜率都不会发生变化。
d d w w = 1 w 1 − 1 = w 0 = 1 (4-28) \frac{\mathrm{d}}{\mathrm{d} w} w=1 w^{1-1}=w^{0}=1 \tag{4-28} dwdw=1w1−1=w0=1(4-28)
4.4.2 带导数符号的数学式的变形
接下来,我们思考一下带导数符号的数学式该如何变形。跟求和符号 Σ \Sigma Σ一样,导数符号 d d w \frac{d}{dw} dwd也作用于式子的右侧。
如下面的 2 w 5 2w^5 2w5所示,当常数出现在 w n w^n wn的前面表示相乘时,我们可以把这个常数提取到导数符号的左侧:
d d w 2 w 5 = 2 d d w w 5 = 2 × 5 w 4 = 10 w 4 \frac{\mathrm{d}}{\mathrm{d} w} 2 w^{5}=2 \frac{\mathrm{d}}{\mathrm{d} w} w^{5}=2 \times 5 w^{4}=10 w^{4} dwd2w5=2dwdw5=2×5w4=10w4
与导数无关的部分(不是 w w w的函数的部分),即使是字符表达式也可以把它提取到导数符号的左侧。
如果 f ( w ) f(w) f(w)中不包含 w w w,则导数为0:
d d w 3 = 0 \frac{d}{dw}3=0 dwd3=0
那么,下式的导数是什么呢?
f ( w ) = a 3 + x b 2 + 2 (4-29) f(w)=a^3+xb^2+2 \tag{4-29} f(w)=a3+xb2+2(4-29)
这个式子里也不包含 w w w,所以导数为0:
当 f ( x ) f(x) f(x)包含多个带 w w w的项时,比如下面这个式子,它的导数是什么呢?
f ( w ) = 2 w 3 + 3 w 2 + 2 f(w)=2w^3+3w^2+2 f(w)=2w3+3w2+2
此时,我们可以一项一项地分别进行导数计算:
d d w f ( w ) = 2 d d w w 3 + 3 d d w w 2 + d d w 2 = 6 w 2 + 6 w (4-30) \frac{\mathrm{d}}{\mathrm{d} w} f(w)=2 \frac{\mathrm{d}}{\mathrm{d} w} w^{3}+3 \frac{\mathrm{d}}{\mathrm{d} w} w^{2}+\frac{\mathrm{d}}{\mathrm{d} w} 2=6 w^{2}+6 w \tag{4-30} dwdf(w)=2dwdw3+3dwdw2+dwd2=6w2+6w(4-30)
4.4.3 复合函数的导数
在机器学习中,很多情况下需要求复合函数的导数,比如:
f ( w ) = f ( g ( w ) ) = g ( w ) 2 (4-31) f(w)=f(g(w))=g(w)^2 \tag{4-31} f(w)=f(g(w))=g(w)2(4-31)
g ( w ) = a w + b (4-32) g(w)=aw+b \tag{4-32} g(w)=aw+b(4-32)
只需简单地将式4-32代入式4-31中,然后展开,即可计算它的导数:
f ( w ) = ( a w + b ) 2 = a 2 w 2 + 2 a w b + b 2 (4-33) f(w)=(aw+b)^2=a^2w^2+2awb+b^2 \tag{4-33} f(w)=(aw+b)2=a2w2+2awb+b2(4-33)
d d w f ( w ) = 2 a 2 w + 2 a b (4-34) \frac{d}{dw}f(w)=2a^2w+2ab \tag{4-34} dwdf(w)=2a2w+2ab(4-34)
4.4.4 复合函数的导数:链式法则
但是,有时式子比较复杂,很难展开。在这种情况下,可以使用链式法则。
链式法则的公式是:
d f d w = d f d g ⋅ d g d w (4-35) \frac{\mathrm{d} f}{\mathrm{~d} w}=\frac{\mathrm{d} f}{\mathrm{~d} g} \cdot \frac{\mathrm{d} g}{\mathrm{~d} w} \tag{4-35} dwdf= dgdf⋅ dwdg(4-35)
接下来,我们借着式4-31和式4-32讲解一下链式法则。
f ( w ) = f ( g ( w ) ) = g ( w ) 2 (4-31) f(w)=f(g(w))=g(w)^2 \tag{4-31} f(w)=f(g(w))=g(w)2(4-31)
g ( w ) = a w + b (4-32) g(w)=aw+b \tag{4-32} g(w)=aw+b(4-32)
首先, d f / d g df/dg df/dg的部分是“ f f f对 g g g求导”的意思,所以可以套用导数公式,得到:
d f d g = d d g g 2 = 2 g (4-36) \frac{\mathrm{d} f}{\mathrm{~d} g}=\frac{\mathrm{d}}{\mathrm{d} g} g^{2}=2 g \tag{4-36} dgdf=dgdg2=2g(4-36)
后面的 d g / d w dg/dw dg/dw是“ g g g对 w w w求导”的意思,所以可以得到
d g d w = d d w ( a w + b ) = a (4-37) \frac{\mathrm{d} g}{\mathrm{~d} w}=\frac{\mathrm{d}}{\mathrm{d} w}(a w+b)=a\tag{4-37} dwdg=dwd(aw+b)=a(4-37)
接下来,把式4-36和式4-37代入式4-35,就可以得到和式4-34的答案一样的答案了:
d f d w = d f d g ⋅ d g d w = 2 g a = 2 ( a w + b ) a = 2 a 2 w + 2 a b (4-38) \frac{\mathrm{d} f}{\mathrm{~d} w}=\frac{\mathrm{d} f}{\mathrm{~d} g} \cdot \frac{\mathrm{d} g}{\mathrm{~d} w}=2 g a=2(a w+b) a=2 a^{2} w+2 a b\tag{4-38} dwdf= dgdf⋅ dwdg=2ga=2(aw+b)a=2a2w+2ab(4-38)
链式法则还可以扩展到三重甚至四重嵌套的复合函数中,比如函数:
f ( w ) = f ( g ( h ( w ) ) ) (4-39) f(w)=f(g(h(w)))\tag{4-39} f(w)=f(g(h(w)))(4-39)
此时,需要使用如下公式:
d f d w = d f d g ⋅ d g d h ⋅ d h d w (4-40) \frac{\mathrm{d} f}{\mathrm{~d} w}=\frac{\mathrm{d} f}{\mathrm{~d} g} \cdot \frac{\mathrm{d} g}{\mathrm{~d} h} \cdot \frac{\mathrm{d} h}{\mathrm{~d} w}\tag{4-40} dwdf= dgdf⋅ dhdg⋅ dwdh(4-40)
4.4.5 基本函数的求导公式
-
y = c ( c 为常数 ) y=c(c为常数) y=c(c为常数)
y ′ = 0 y'=0 y′=0 -
y = x n y=x^n y=xn
y ′ = n x ( n − 1 ) y'=nx^{(n-1)} y′=nx(n−1) -
y = a x y=a^x y=ax
y ′ = a x ln a y'=a^x\ln a y′=axlna
特例: y = e x 时, y ′ = e x 特例:y=e^x时,y'=e^x 特例:y=ex时,y′=ex -
y = log a x y=\log_ax y=logax
y ′ = 1 x ln a y'=\frac {1}{x \ln a} y′=xlna1
特例: a = e 时, y ′ = 1 / x 特例:a=e时,y'=1/x 特例:a=e时,y′=1/x
4.5 偏导数
4.5.1 偏导数的概念
机器学习中不仅会用到导数,还会用到偏导数。
思考一下多变量函数,比如关于 w 0 w_0 w0和 w 1 w_1 w1的函数:
f ( w 0 , w 1 ) = w 0 2 + 2 w 0 w 1 + 3 (4-41) f\left(w_{0}, w_{1}\right)=w_{0}^{2}+2 w_{0} w_{1}+3\tag{4-41} f(w0,w1)=w02+2w0w1+3(4-41)
对于式4-41,如果只对其中一个变量(比如 w 0 w_0 w0)求导,而将其他变量(这里是 w 1 w_1 w1)当作常数,那么求出的就是偏导数。
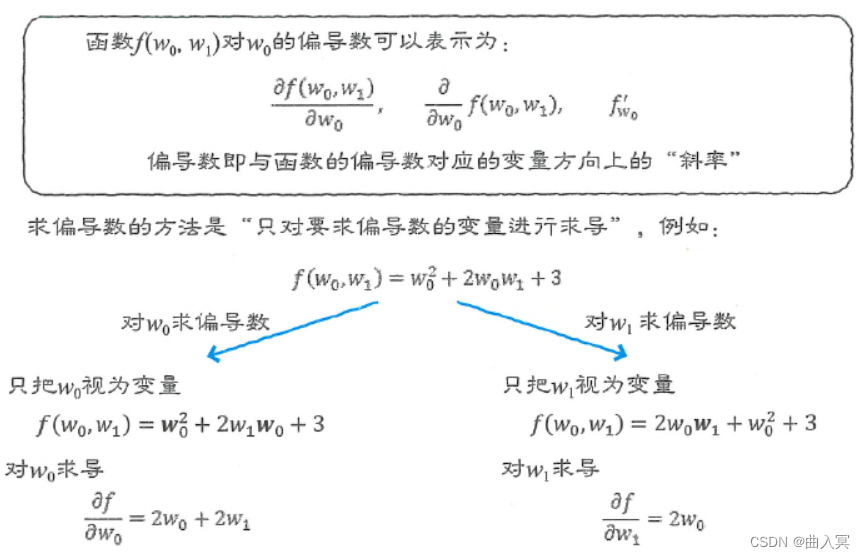
图4-8 偏导数
“ f f f对 w 0 w_0 w0的偏导数”的数学式是:
∂ f ∂ w 0 , ∂ ∂ w 0 f , f w 0 ′ (4-42) \frac{\partial f}{\partial w_{0}}, \frac{\partial}{\partial w_{0}} f, f_{w_{0}}^{\prime}\tag{4-42} ∂w0∂f,∂w0∂f,fw0′(4-42)
备注:偏导数的表示符号为:$\partial $ 。$\partial 读作 r o u n d 。 读作round。 读作round。\partial 是希腊字母 是希腊字母 是希腊字母\delta 的古典写法,数学里只用作表示偏导数的记号,在表示偏导数的时候,一般不念字母名称,大多念作“偏”(例如 的古典写法,数学里只用作表示偏导数的记号,在表示偏导数的时候,一般不念字母名称,大多念作“偏”(例如 的古典写法,数学里只用作表示偏导数的记号,在表示偏导数的时候,一般不念字母名称,大多念作“偏”(例如z 对 对 对x 的偏导数 , 念作“偏 的偏导数,念作“偏 的偏导数,念作“偏z 偏 偏 偏x$”)。
求偏导数的方法是“只对要求偏导数的变量进行求导”,实际上它的求导过程与普通的导数(常微分)是一样的。
例如,以前面的式4-41中的 ∂ f / ∂ w 0 \partial f / \partial w_{0} ∂f/∂w0来说,就是只关注其中的 w 0 w_0 w0,像下式这样思考:
f ( w 0 , w 1 ) = w 0 2 + 2 w 1 w 0 + 3 (4-43) f\left(w_{0}, w_{1}\right)=w_{0}^{2}+2 w_{1} w_{0}+3\tag{4-43} f(w0,w1)=w02+2w1w0+3(4-43)
套用导数公式之后,得到:
∂ f ∂ w 0 = 2 w 0 + 2 w 1 (4-44) \frac{\partial f}{\partial w_{0}}=2 w_{0}+2 w_{1}\tag{4-44} ∂w0∂f=2w0+2w1(4-44)
而对于式4-41中的 ∂ f / ∂ w 1 \partial f / \partial w_{1} ∂f/∂w1,则只关注其中的 w 1 w_1 w1,像下式这样解释:
f ( w 0 , w 1 ) = 2 w 0 w 1 + w 0 2 + 3 (4-45) f\left(w_{0}, w_{1}\right)=2 w_{0} w_{1}+w_{0}^{2}+3\tag{4-45} f(w0,w1)=2w0w1+w02+3(4-45)
然后,就可以得到:
∂ f ∂ w 1 = 2 w 0 (4-46) \frac{\partial f}{\partial w_{1}}=2 w_{0}\tag{4-46} ∂w1∂f=2w0(4-46)
4.5.2 偏导数的图形
偏导数的图形是什么样的呢?
f ( w 0 , w 1 ) f(w_0,w_1) f(w0,w1)的函数可以使用matplotlib库绘制的三维图形或等高线图形表示。实际绘制之后会发现,它的图形就像一个两个角被提起来的方巾。
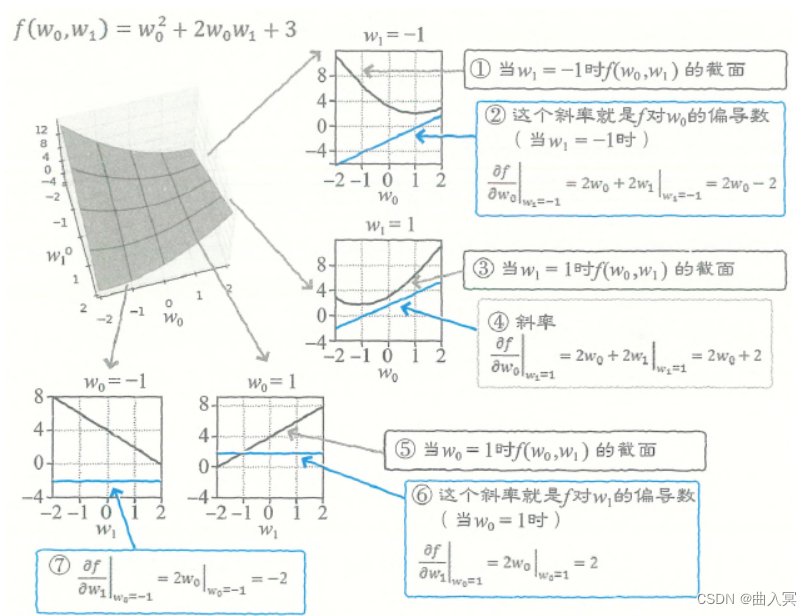
图4-9 偏导数的图形意义
为了理解 ∂ f / ∂ w 0 \partial f / \partial w_{0} ∂f/∂w0,我们可以在与 w 0 w_0 w0轴平行的方向上把 f f f切开,然后观察 f f f的截面(图4-9①)。
截面是一个向下凸出(向上开口)的二次函数,它的曲线斜率可以通过式4-44求得,式子为 ∂ f / ∂ w 0 = 2 w 0 + 2 w 1 \partial f / \partial w_{0}=2w_0+2w_1 ∂f/∂w0=2w0+2w1。
当在 w 1 = − 1 w_1=-1 w1=−1的平面上切开时,把 w 1 = − 1 w_1=-1 w1=−1代入式4-44,即可得到当 w 1 = − 1 w_1=-1 w1=−1时斜率的计算式。
把 w 1 = − 1 w_1=-1 w1=−1代入 ∂ f / ∂ w 0 \partial f / \partial w_{0} ∂f/∂w0之后得到:
∂ f ∂ w 0 ∣ w 1 = − 1 (4-47) \left.\frac{\partial f}{\partial w_{0}}\right|_{w_{1}=-1}\tag{4-47} ∂w0∂f w1=−1(4-47)
这里,使用式4-44的结果,可以像下式这样去计算(图4-9②)。这是一条斜率为2、截距为-2的直线:
∂ f ∂ w 0 ∣ w 1 = − 1 = 2 w 0 + 2 w 1 ∣ w 1 = − 1 = 2 w 0 − 2 (4-48) \left.\frac{\partial f}{\partial w_{0}}\right|_{w_{1}=-1}=2 w_{0}+\left.2 w_{1}\right|_{w_{1}=-1}=2 w_{0}-2\tag{4-48} ∂w0∂f w1=−1=2w0+2w1∣w1=−1=2w0−2(4-48)
平行于 w 0 w_0 w0轴的平面有无数个。比如,当在 w 1 = 1 w_1=1 w1=1的平面上切开时, f f f的截面如图4-9③所示,截面的斜率是(图4-9④):
∂ f ∂ w 0 ∣ w 1 = − 1 = 2 w 0 + 2 w 1 ∣ w 1 = 1 = 2 w 0 + 2 (4-50) \left.\frac{\partial f}{\partial w_{0}}\right|_{w_{1}=-1}=2 w_{0}+\left.2 w_{1}\right|_{w_{1}=1}=2 w_{0}+2\tag{4-50} ∂w0∂f w1=−1=2w0+2w1∣w1=1=2w0+2(4-50)
而 ∂ f / ∂ w 1 \partial f / \partial w_{1} ∂f/∂w1是一个平行于 w 1 w_1 w1轴的 f f f的截面,这个截面是一条直线。比如,当在 w 0 = 1 w_0=1 w0=1的平面上切开时,得到的截面如图4-12⑤所示,它的斜率是(图4-12⑥):
∂ f ∂ w 1 ∣ w 0 = 1 = 2 w 0 ∣ w 0 = 1 = 2 (4-50) \left.\frac{\partial f}{\partial w_{1}}\right|_{w_{0}=1}=\left.2 w_{0}\right|_{w_{0}=1}=2\tag{4-50} ∂w1∂f w0=1=2w0∣w0=1=2(4-50)
又如,当在 w 0 = − 1 w_0=-1 w0=−1的平面上切开时,得到的截面的斜率是(图4-12⑦):
∂ f ∂ w 1 ∣ w 0 = 1 = 2 w 0 ∣ w 0 = − 1 = − 2 (4-51) \left.\frac{\partial f}{\partial w_{1}}\right|_{w_{0}=1}=\left.2 w_{0}\right|_{w_{0}=-1}=-2\tag{4-51} ∂w1∂f w0=1=2w0∣w0=−1=−2(4-51)
总的来说,对 w 0 w_0 w0和 w 1 w_1 w1的偏导数就是分别求出 w 0 w_0 w0方向的斜率和 w 1 w_1 w1方向的斜率。
这两个斜率的组合可以解释为向量。这就是 f f f对 w w w的梯度(梯度向量,gradient),梯度表示的是斜率最大的方向及其大小。
∇ w f = [ ∂ f ∂ w 0 ∂ f ∂ w 1 ] (4-52) \nabla_{w} f=\left[\begin{array}{c} \frac{\partial f}{\partial w_{0}} \\ \frac{\partial f}{\partial w_{1}} \tag{4-52} \end{array}\right] ∇wf=[∂w0∂f∂w1∂f](4-52)
梯度算子∇应该如何来读呢?詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)为∇发明了发音,叫作“纳布拉(Nabla)。Nabla原指一种希伯来竖琴,外形酷似倒三角。
4.5.3 梯度的图形
下面实际绘制一下梯度的图形。以下代码绘制了 f f f的等高线(图4-10左),并通过箭头绘制了把 w w w的空间分为网格状时各点的梯度 ∇ w f \nabla_{w} f ∇wf (图4-10右)。
# 代码清单 4-2-(2)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inlinedef f(w0, w1): # (A) 定义函数freturn w0**2 + 2 * w0 * w1 + 3def df_dw0(w0, w1): # (B) 定义用于返回w0方向的偏导数的函数df_dw0return 2 * w0 + 2 * w1def df_dw1(w0, w1): # (C) 定义用于返回w1方向的偏导数的函数df_dwlreturn 2 * w0 + 0 * w1w_range = 2
dw = 0.25
w0 = np.arange(-w_range, w_range + dw, dw)
w1 = np.arange(-w_range, w_range + dw, dw)ww0, ww1 = np.meshgrid(w0, w1) # (D) 将网格状分布的w0和w1存储在二维数组ww0和ww1中ff = np.zeros((len(w0), len(w1)))
dff_dw0 = np.zeros((len(w0), len(w1)))
dff_dw1 = np.zeros((len(w0), len(w1)))
for i0 in range(len(w0)):for i1 in range(len(w1)):ff[i1, i0] = f(w0[i0], w1[i1])dff_dw0[i1, i0] = df_dw0(w0[i0], w1[i1])dff_dw1[i1, i0] = df_dw1(w0[i0], w1[i1])
# (E) 根据ww0和wwl计算f和偏导数的值,并将值存储在ff和dff_dw0、dff_dw1中plt.figure(figsize=(10, 4.5))
plt.subplots_adjust(wspace=0.3)
plt.subplot(1, 2, 1)
cont = plt.contour(ww0, ww1, ff, 10, colors='k') # (F) 将ff显示为等高线
cont.clabel(fmt='%d', fontsize=8)
plt.xticks(range(-w_range, w_range + 1, 1))
plt.yticks(range(-w_range, w_range + 1, 1))
plt.xlim(-w_range - 0.5, w_range + 0.5)
plt.ylim(-w_range - 0.5, w_range + 0.5)
plt.xlabel('$w_0$', fontsize=14)
plt.ylabel('$w_1$', fontsize=14)plt.subplot(1, 2, 2)
plt.quiver(ww0, ww1, dff_dw0, dff_dw1) # (G) 将梯度显示为箭头
plt.xlabel('$w_0$', fontsize=14)
plt.ylabel('$w_1$', fontsize=14)
plt.xticks(range(-w_range, w_range + 1, 1))
plt.yticks(range(-w_range, w_range + 1, 1))
plt.xlim(-w_range - 0.5, w_range + 0.5)
plt.ylim(-w_range - 0.5, w_range + 0.5)
plt.show()
输出结果:
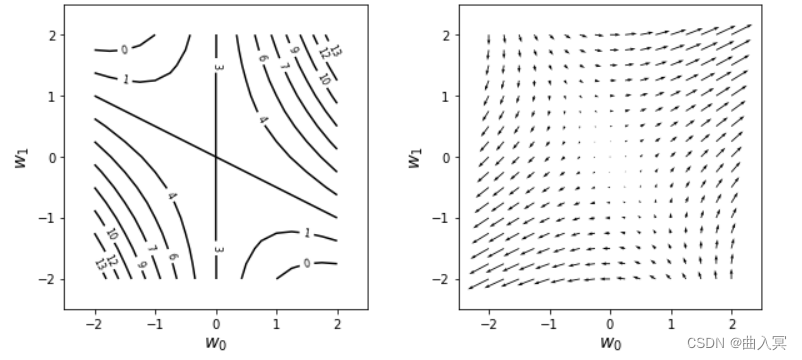
以上代码首先在(A)处定义了函数 f f f,然后在(B)处定义了用于返回 w 0 w_0 w0方向的偏导数的函数df_dw0,在©处定义了用于返回 w 1 w_1 w1方向的偏导数的函数df_dwl。
(D)处的ww0, ww1 = np.meshgrid(w0, w1)将网格状分布的 w 0 w_0 w0和 w 1 w_1 w1存储在了二维数组ww0和ww1中。(E)用于根据ww0和wwl计算 f f f和偏导数的值,并将值存储在ff和dff_dw0、dff_dw1中。(F)用于将ff显示为等高线,(G)用于将梯度显示为箭头。
用于显示箭头的代码(G)是通过plt.quiver(ww0, ww1, dff_dw0, dff_dw1)绘制从坐标点(ww0, wwl)到方向(dff_dw0, dff_dw1)的箭头的。
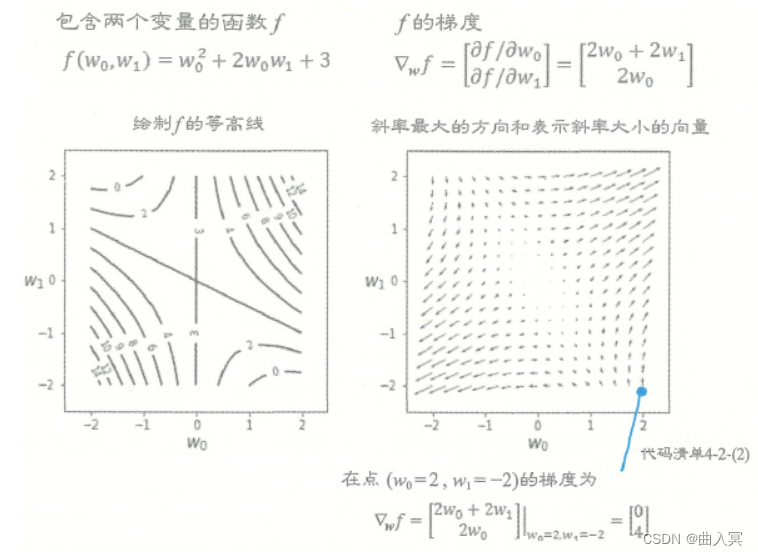
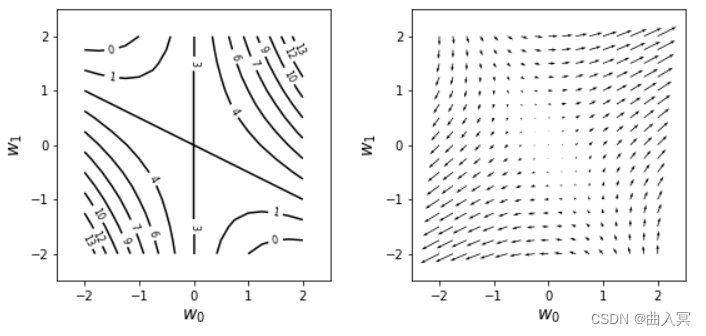
图4-10梯度向量
通过图4-10左侧的 f f f的等高线图形上的数值,我们可以想象到 f f f的地形是右上方和左下方较髙,左上方和右下方较低。图4-10右侧是这种地形的梯度,可以看到箭头朝向的是各个点中斜面较高的方向,而且斜面越陡(等高线间隔越短),箭头越长。
观察可知,箭头无论从哪个地点开始,都总是朝向图形中地形较高的部分。相反,箭尾总是朝向地形较低的部分。因此,梯度是用于寻找函数的最大点或最小点的一个重要概念。在机器学习中,在求误差函数的最小点时会使用误差函数的梯度。
4.5.4 多变量的复合函数的偏导数
当嵌套的是多变量函数时,该怎么求导呢?我们会在推导多层神经网络的学习规则时遇到这个问题。
比如, g 0 g_0 g0和 g 1 g_1 g1都是关于 w 0 w_0 w0和 w 1 w_1 w1的函数, f f f是关于函数 g 0 g_0 g0和 g 1 g_1 g1的函数。现在我们使用链式法则来表示 f f f对 w 0 w_0 w0和 w 1 w_1 w1的偏导数(图4-11):
f ( g 0 ( w 0 , w 1 ) , g 1 ( w 0 , w 1 ) ) (4-53) f\left(g_{0}\left(w_{0}, w_{1}\right), g_{1}\left(w_{0}, w_{1}\right)\right)\tag{4-53} f(g0(w0,w1),g1(w0,w1))(4-53)
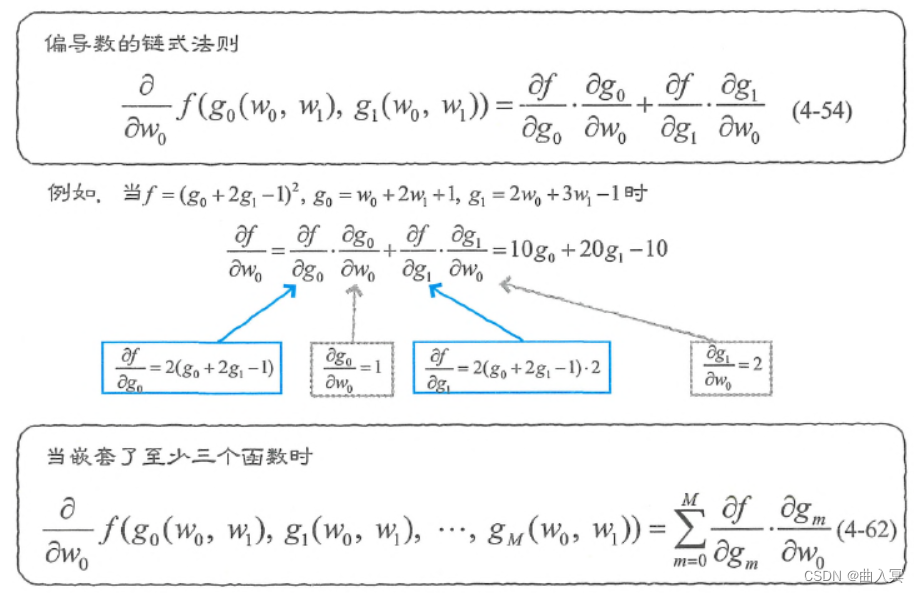
图4-11 偏导数的链式法则
下面先说一下结论,对 w 0 w_0 w0求偏导数的式子是:
∂ ∂ w 0 f ( g 0 ( w 0 , w 1 ) , g 1 ( w 0 , w 1 ) ) = ∂ f ∂ g 0 ⋅ ∂ g 0 ∂ w 0 + ∂ f ∂ g 1 ⋅ ∂ g 1 ∂ w 0 (4-54) \frac{\partial}{\partial w_{0}} f\left(g_{0}\left(w_{0}, w_{1}\right), g_{1}\left(w_{0}, w_{1}\right)\right)=\frac{\partial f}{\partial g_{0}} \cdot \frac{\partial g_{0}}{\partial w_{0}}+\frac{\partial f}{\partial g_{1}} \cdot \frac{\partial g_{1}}{\partial w_{0}}\\ \tag{4-54} ∂w0∂f(g0(w0,w1),g1(w0,w1))=∂g0∂f⋅∂w0∂g0+∂g1∂f⋅∂w0∂g1(4-54)
对 w 1 w_1 w1求偏导数的式子是:
∂ ∂ w 1 f ( g 0 ( w 0 , w 1 ) , g 1 ( w 0 , w 1 ) ) = ∂ f ∂ g 0 ⋅ ∂ g 0 ∂ w 1 + ∂ f ∂ g 1 ⋅ ∂ g 1 ∂ w 1 (4-55) \frac{\partial}{\partial w_{1}} f\left(g_{0}\left(w_{0}, w_{1}\right), g_{1}\left(w_{0}, w_{1}\right)\right)=\frac{\partial f}{\partial g_{0}} \cdot \frac{\partial g_{0}}{\partial w_{1}}+\frac{\partial f}{\partial g_{1}} \cdot \frac{\partial g_{1}}{\partial w_{1}}\\ \tag{4-55} ∂w1∂f(g0(w0,w1),g1(w0,w1))=∂g0∂f⋅∂w1∂g0+∂g1∂f⋅∂w1∂g1(4-55)
比如,当 f f f如下式时,该如何求解 ∂ f ∂ w 0 \frac{\partial f}{\partial w_{0}} ∂w0∂f呢?
f = ( g 0 + 2 g 1 − 1 ) 2 , g 0 = w 0 + 2 w 1 + 1 , g 1 = 2 w 0 + 3 w 1 − 1 (4-56) f=\left(g_{0}+2 g_{1}-1\right)^{2}, g_{0}=w_{0}+2 w_{1}+1, g_{1}=2 w_{0}+3 w_{1}-1\tag{4-56} f=(g0+2g1−1)2,g0=w0+2w1+1,g1=2w0+3w1−1(4-56)
此时,式4-54的构成要素就变成了:
∂ f ∂ g 0 = 2 ( g 0 + 2 g 1 − 1 ) (4-57) \frac{\partial f}{\partial g_{0}}=2\left(g_{0}+2 g_{1}-1\right)\tag{4-57} ∂g0∂f=2(g0+2g1−1)(4-57)
∂ f ∂ g 1 = 2 ( g 0 + 2 g 1 − 1 ) ⋅ 2 (4-58) \frac{\partial f}{\partial g_{1}}=2\left(g_{0}+2 g_{1}-1\right) \cdot 2 \tag{4-58} ∂g1∂f=2(g0+2g1−1)⋅2(4-58)
∂ g 0 ∂ w 0 = 1 (4-59) \frac{\partial g_{0}}{\partial w_{0}}=1 \tag{4-59} ∂w0∂g0=1(4-59)
∂ g 1 ∂ w 0 = 2 (4-60) \frac{\partial g_{1}}{\partial w_{0}}=2 \tag{4-60} ∂w0∂g1=2(4-60)
把它们代入式4-54,即可像下式这样求解,请注意,式4-57和式4-58也使用了链式法则:
∂ f ∂ w 0 = 2 ( g 0 + 2 g 1 − 1 ) ⋅ 1 + 2 ( g 0 + 2 g 1 − 1 ) ⋅ 2 ⋅ 2 = 10 g 0 + 20 g 1 − 10 (4-61) \frac{\partial f}{\partial w_{0}}=2\left(g_{0}+2 g_{1}-1\right) \cdot 1+2\left(g_{0}+2 g_{1}-1\right) \cdot 2 \cdot 2=10 g_{0}+20 g_{1}-10\tag{4-61} ∂w0∂f=2(g0+2g1−1)⋅1+2(g0+2g1−1)⋅2⋅2=10g0+20g1−10(4-61)
在实际推导神经网络的学习规则时,使用的往往是像 f ( g 0 ( w 0 , w 1 ) , g 1 ( w 0 , w 1 f(g_0(w_0,w_1),g_1(w_0,w_1 f(g0(w0,w1),g1(w0,w1),…, g m ( w 0 , w 1 ) g_m(w_0,w_1) gm(w0,w1)这样嵌套了至少两个函数的函数。此时,链式法则是:
∂ f ∂ w 0 = ∂ f ∂ g 0 ⋅ ∂ g 0 ∂ w 0 + ∂ f ∂ g 1 ⋅ ∂ g 1 ∂ w 0 + ⋯ + ∂ f ∂ g M ⋅ ∂ g M ∂ w 0 = ∑ m = 0 M ∂ f ∂ g m ⋅ ∂ g m ∂ w 0 (4-62) \frac{\partial f}{\partial w_{0}}=\frac{\partial f}{\partial g_{0}} \cdot \frac{\partial g_{0}}{\partial w_{0}}+\frac{\partial f}{\partial g_{1}} \cdot \frac{\partial g_{1}}{\partial w_{0}}+\cdots+\frac{\partial f}{\partial g_{M}} \cdot \frac{\partial g_{M}}{\partial w_{0}}=\sum_{m=0}^{M} \frac{\partial f}{\partial g_{m}} \cdot \frac{\partial g_{m}}{\partial w_{0}}\tag{4-62} ∂w0∂f=∂g0∂f⋅∂w0∂g0+∂g1∂f⋅∂w0∂g1+⋯+∂gM∂f⋅∂w0∂gM=m=0∑M∂gm∂f⋅∂w0∂gm(4-62)
4.5.5 交换求和与求导的顺序
在机器学习中,计算时常常需要对一个用求和符号表示的函数求导,比如(本节将偏导数也称为导数):
∂ ∂ w ∑ n = 1 3 n w 2 (4-63) \frac{\partial}{\partial w} \sum_{n=1}^{3} n w^{2}\tag{4-63} ∂w∂n=1∑3nw2(4-63)
单纯地说,应该可以先求和再求导:
∂ ∂ w ( w 2 + 2 w 2 + 3 w 2 ) = ∂ ∂ w 6 w 2 = 12 w \frac{\partial}{\partial w}\left(w^{2}+2 w^{2}+3 w^{2}\right)=\frac{\partial}{\partial w} 6 w^{2}=12 w ∂w∂(w2+2w2+3w2)=∂w∂6w2=12w
但是,实际上即使先求出各项的导数再求和,答案也是一样的:
∂ ∂ w ( w 2 + 2 w 2 + 3 w 2 ) = ∂ ∂ w w 2 + ∂ ∂ w 2 w 2 + ∂ ∂ w 3 w 2 = 2 w + 4 w + 6 w = 12 w \frac{\partial}{\partial w}\left(w^{2}+2 w^{2}+3 w^{2}\right) =\frac{\partial}{\partial w} w^{2}+\frac{\partial}{\partial w} 2 w^{2}+\frac{\partial}{\partial w} 3 w^{2}=2w+4w+6w=12w ∂w∂(w2+2w2+3w2)=∂w∂w2+∂w∂2w2+∂w∂3w2=2w+4w+6w=12w
如果使用求和符号表示上述计算过程,则具体为:
∂ ∂ w w 2 + 2 ∂ ∂ w w 2 + 3 ∂ ∂ w w 2 = ∑ n = 1 3 ∂ ∂ w n w 2 (4-64) \frac{\partial}{\partial w} w^{2}+2 \frac{\partial}{\partial w} w^{2}+3 \frac{\partial}{\partial w} w^{2}=\sum_{n=1}^{3} \frac{\partial}{\partial w} n w^{2}\tag{4-64} ∂w∂w2+2∂w∂w2+3∂w∂w2=n=1∑3∂w∂nw2(4-64)
因此,根据式4-63和式4-64,下式成立:
∂ ∂ w ∑ n = 1 3 n w 2 = ∑ n = 1 3 ∂ ∂ w n w 2 (4-65) \frac{\partial}{\partial w} \sum_{n=1}^{3} n w^{2}=\sum_{n=1}^{3} \frac{\partial}{\partial w} n w^{2}\tag{4-65} ∂w∂n=1∑3nw2=n=1∑3∂w∂nw2(4-65)
我们可以把它一般化为下式。如图4-12所示,可以把导数符号提取到求和符号的右侧,先进行求导计算。
∂ ∂ w ∑ n f n ( w ) = ∑ n ∂ ∂ w f n ( w ) (4-66) \frac{\partial}{\partial w} \sum_{n} f_{n}(w)=\sum_{n} \frac{\partial}{\partial w} f_{n}(w)\tag{4-66} ∂w∂n∑fn(w)=n∑∂w∂fn(w)(4-66)
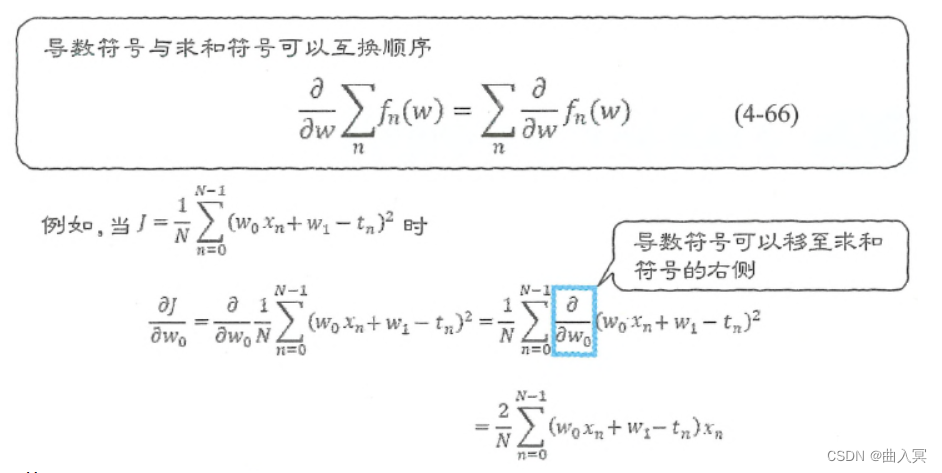
图4-12 导数符号和求和符号的互换
我们常常遇到先求导可以令计算更轻松,或者只能求导的情况。因此,机器学习中经常会用到式4-66。
比如,我们使用下式思考一下:
J = 1 N ∑ n = 0 N − 1 ( w 0 x n + w 1 − t n ) 2 (4-67) J=\frac{1}{N} \sum_{n=0}^{N-1}\left(w_{0} x_{n}+w_{1}-t_{n}\right)^{2}\tag{4-67} J=N1n=0∑N−1(w0xn+w1−tn)2(4-67)
在求上述函数对 w 0 w_0 w0的导数时,要使用式4-66将导数符号移至求和符号的右侧:
∂ J ∂ w 0 = ∂ ∂ w 0 1 N ∑ n = 0 N − 1 ( w 0 x n + w 1 − t n ) 2 = 1 N ∑ n = 0 N − 1 ∂ ∂ w 0 ( w 0 x n + w 1 − t n ) 2 (4-68) \frac{\partial J}{\partial w_{0}} =\frac{\partial}{\partial w_{0}} \frac{1}{N} \sum_{n=0}^{N-1}\left(w_{0} x_{n}+w_{1}-t_{n}\right)^{2} =\frac{1}{N} \sum_{n=0}^{N-1} \frac{\partial}{\partial w_{0}}\left(w_{0} x_{n}+w_{1}-t_{n}\right)^{2}\tag{4-68} ∂w0∂J=∂w0∂N1n=0∑N−1(w0xn+w1−tn)2=N1n=0∑N−1∂w0∂(w0xn+w1−tn)2(4-68)
然后,求出导数,得到:
= 1 N ∑ n = 0 N − 1 2 ( w 0 x n + w 1 − t n ) x n = 2 N ∑ n = 0 N − 1 ( w 0 x n + w 1 − t n ) x n (4-69) \begin{array}{l} =\frac{1}{N} \sum_{n=0}^{N-1} 2\left(w_{0} x_{n}+w_{1}-t_{n}\right) x_{n}\\ =\frac{2}{N} \sum_{n=0}^{N-1}\left(w_{0} x_{n}+w_{1}-t_{n}\right) x_{n}\tag{4-69} \end{array} =N1∑n=0N−12(w0xn+w1−tn)xn=N2∑n=0N−1(w0xn+w1−tn)xn(4-69)
这里,在计算 ∂ ∂ w 0 ( w 0 x n + w 1 − t n ) 2 = 2 ( w 0 x n + w 1 − t n ) x n \frac{\partial}{\partial w_{0}}\left(w_{0} x_{n}+w_{1}-t_{n}\right)^{2}=2\left(w_{0} x_{n}+w_{1}-t_{n}\right) x_{n} ∂w0∂(w0xn+w1−tn)2=2(w0xn+w1−tn)xn时,我们使用了链式法则的式子,即 f = g 2 , g = w 0 x n + w 1 − t n f=g^{2}, \quad g=w_{0} x_{n}+w_{1}-t_{n} f=g2,g=w0xn+w1−tn。

![[ 蓝桥杯Web真题 ]-布局切换](https://img-blog.csdnimg.cn/img_convert/eb91b2d102d8af1da7def68abf95e729.png)