一 什么是回溯算法
回溯算法(Backtracking Algorithm)是一种用于解决组合优化问题的算法,它通过逐步构建候选解并进行验证,以寻找所有满足特定条件的解。回溯算法通常应用于在给定约束条件下枚举所有可能解的问题,如组合、排列、子集等。
回溯算法的基本思想是通过递归的方式进行搜索,每一步都尝试扩展当前的解,直到找到满足条件的解或者确定无解。在搜索的过程中,如果当前的解不满足约束条件,就会回溯到上一步进行其他选择,继续搜索。
回溯算法的一般步骤如下:
- 定义问题的解空间,确定问题的约束条件。
- 通过递归的方式搜索解空间,每一步都进行选择,并进行约束条件的检查。
- 如果当前的选择满足约束条件,则继续递归地进行下一步选择。
- 如果当前的选择不满足约束条件,进行回溯,撤销当前选择,返回上一步继续搜索其他选择。
- 当搜索完成后,得到所有满足条件的解。
回溯算法的时间复杂度通常较高,因为它需要枚举所有可能的解。在某些情况下,可以通过剪枝等优化策略来减少搜索空间,提高算法效率。
回溯算法在很多问题中都有应用,例如八皇后问题、0-1背包问题、图的遍历等。它是一种非常经典和常用的算法思想,对于解决组合优化问题具有重要的作用。
通常解该类题目时,我们要确定解的空间,从而很好的利用回溯算法来解决该类题目。
二 何为解空间
解空间(Solution Space)是指在给定问题的约束条件下,所有可能的解的集合。它包含了问题的所有合法解。
解空间的具体形式取决于问题的性质和约束条件。对于某些问题,解空间可能是一个有限的集合,例如在数独游戏中,解空间是由符合数独规则的所有数字填充方案组成的集合。而对于其他问题,解空间可能是一个无限的集合,例如在连续优化问题中,解空间是由实数构成的无限维空间。
解空间是问题求解的关键概念之一。在解决问题时,我们通常需要在解空间中搜索满足特定条件的解。回溯算法、枚举法、剪枝算法等求解方法都是基于对解空间的搜索。
解空间的大小直接影响了问题的复杂性和求解算法的效率。如果解空间非常大,问题的求解可能会非常困难,需要耗费更多的时间和资源。因此,在实际应用中,优化算法常常通过剪枝、启发式搜索等技术来减小解空间的规模,以提高求解效率。
总之,解空间是问题求解中描述所有可能解的概念,通过搜索解空间,我们可以找到满足问题要求的解或者找到最优解。
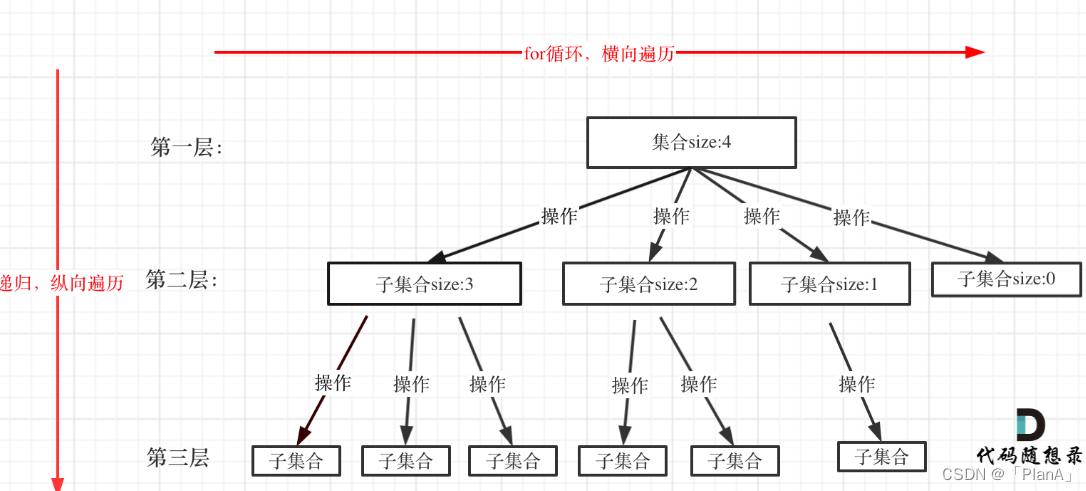
对于大多数该类问题的解空间都是树的形式,集合的大小构成了树的宽度,递归的深度构成的树的深度。
三 回溯算法的模板
下面是回溯算法的一般模板:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {//横向遍历处理节点;//这里一般可能进行剪枝操作backtracking(路径,选择列表); // 递归,纵向遍历回溯,撤销处理结果}
}这是一个基本的回溯算法模板,其中的关键点包括:
-
定义终止条件:当满足终止条件时,表示找到了一个解或者不再需要继续搜索,可以进行相应的操作,如输出结果或返回。
-
遍历选择列表:遍历所有可能的选择,通常使用循环结构,对于每个选择,进行相应的操作。
-
做出选择:根据当前选择,更新状态或路径,表示对问题的一次选择。
-
递归进入下一层决策树:根据当前选择,进入下一层决策树,即进行下一步的选择。
-
撤销选择:在回溯到上一层之前,需要撤销当前选择,恢复状态或路径,以便进行下一个选择。
在实际应用中,根据具体问题的不同,模板中的代码需要进行相应的修改和扩展,以适应问题的特点和约束条件。同时,通过剪枝、优化等技巧,可以对模板进行改进,提高算法的效率。
需要注意的是,回溯算法是一种暴力搜索的方法,解空间的规模很大时,可能会导致算法效率低下。因此,在使用回溯算法时,需要根据问题的规模和特点进行合理的优化和剪枝,以提高算法的性能。
四 回溯算法例题之N皇后问题
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n 皇后问题 研究的是如何将
n个皇后放置在n×n的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数
n,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中'Q'和'.'分别代表了皇后和空位。
4*4的棋盘摆放结果如下:

解题思路:
定义一个 N × N 的棋盘,使用一个二维数组或其他数据结构表示。初始化棋盘的所有位置为空。
从第一行开始,逐行放置皇后。对于每一行,遍历该行的每一个位置,尝试将皇后放置在当前位置。
在放置皇后之前,检查是否满足以下条件:
- 当前位置的同一列没有其他皇后。
- 当前位置的左上方和右上方(对角线)没有其他皇后。
如果满足上述条件,将皇后放置在当前位置,并将该位置标记为已占用。
继续递归地处理下一行,重复步骤 3 和步骤 4。
如果已经放置了 N 个皇后,表示找到了一个可行解,将该解保存起来。
回溯到上一步,撤销对当前位置的选择,继续尝试下一个位置。
当所有的位置都尝试完毕或者已经找到了所有的可行解时,算法结束。
返回所有的可行解。
我们先以3*3的棋盘来看它的解空间,如图所示:
不难看出解空间对应的是树的结构,我们可以套用模板进行解决:
void Backtrack(char bord[][N],int n,int row){if(row>=n){//递归出口print(bord,n);//如果满足直接打印结果count++;//用来记录解的数量printf("\n");return ;}else{for(int colum=0;colum<n;colum++){//横向遍历if(isselect(bord,row,colum,n)){//如果满足放置条件bord[row][colum] = 'Q';Backtrack(bord,n,row+1);//进行递归,选择下一行的格子bord[row][colum] = '*';//回溯}}}
}【完整代码】
#include <stdio.h>
#include <stdbool.h>
#define N 100int count=0;
void print(char bord[][N],int n){for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(bord[i][j] == 'Q'){printf(" Q");}else{printf(" *");} }printf("\n");}
}bool isselect(char bord[][N], int row, int colum,int n) {for(int j=0;j<row;j++){//判断列if(bord[j][colum]=='Q'){return false;}}for(int i=row,j=colum;i>=0&&j>=0;i--,j--){//判断左上角if(bord[i][j]=='Q'){return false;}}for(int i=row,j=colum;i>=0&&j<n;i--,j++){//判断右上角if(bord[i][j]=='Q'){return false;}}return true;}void Backtrack(char bord[][N],int n,int row){if(row>=n){print(bord,n);count++;printf("\n");return ;}else{for(int colum=0;colum<n;colum++){if(isselect(bord,row,colum,n)){bord[row][colum] = 'Q';Backtrack(bord,n,row+1);bord[row][colum] = '*';}}}
}int main()
{int n;printf("请输入皇后个数:\n");scanf("%d",&n);char bord[N][N]={'*'};printf("皇后摆放形式如下:\n");Backtrack(bord,n,0);printf("%d后问题共有%d种摆放方案 ",n,count);return 0;
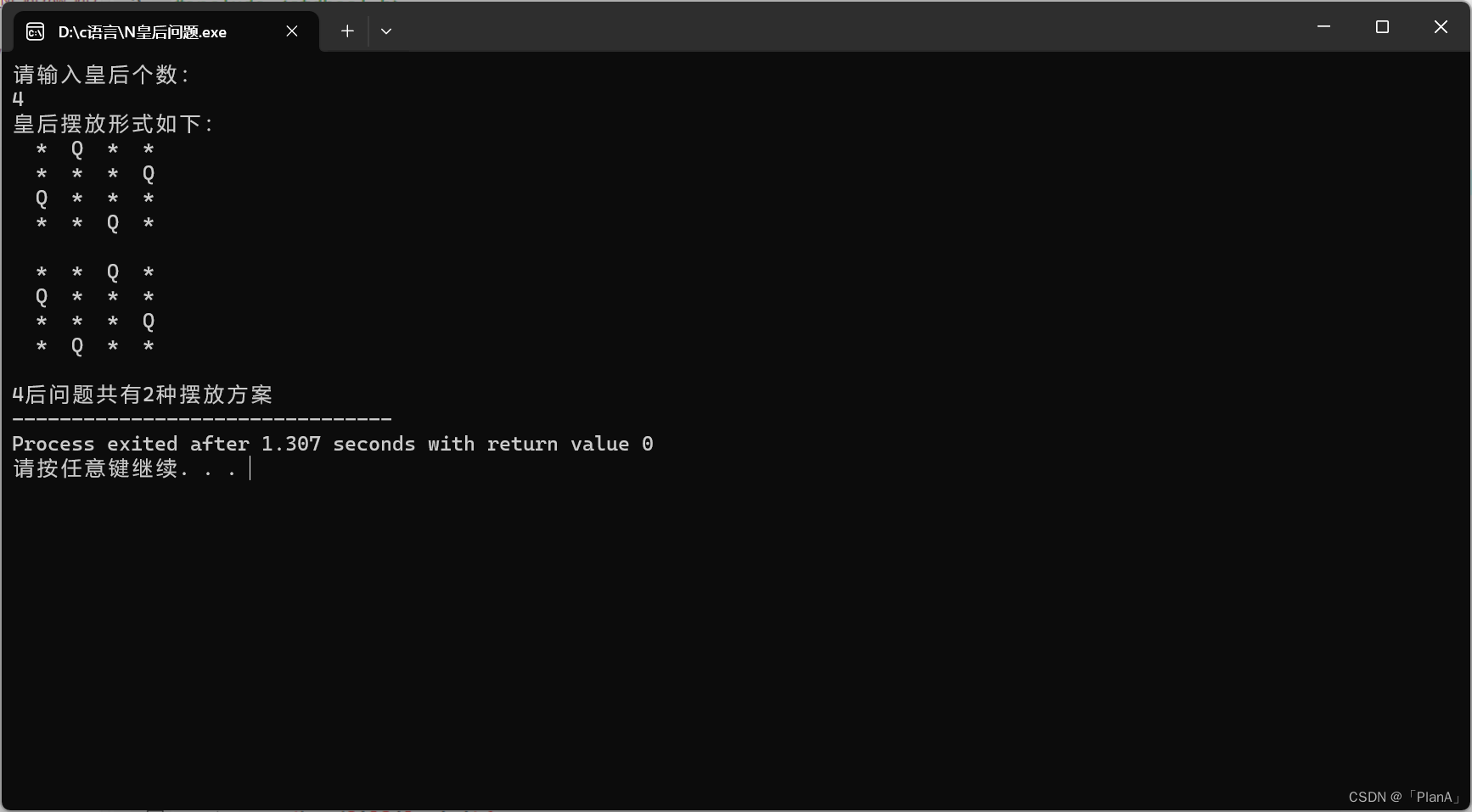
}【运行效果】

部分资料参考:代码随想录;