归并排序
归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并.
核心步骤讲解
归并排序的核心步骤如下:

可以看出,这算法的核心逻辑就是类似小学语文学文章的一种结构的"总-分-总".
让我们来具体剖析一下,来看看它的思路:
拆分过程:以10 6 7 1这一组为例来看一下拆分过程(核心:使用start, end, mid分别表示开头结尾和中间) :

合并过程:让我么以6,10/1,7这一组为例,来看一下合并过程:最主要的地方就在于传入两组要合并的组,然后创建一个新的数组tmpArr,存放要合并的两个组元素,并将tmpArr中的内容放在源数组中对应位置.

下面是代码:
public class MergeSort {public static void mergeSort(int[] arr) {mergeSortFun(arr, 0, arr.length - 1);}public static void mergeSortFun(int[] arr, int start, int end) {//当start和end重合之后,结束递归if(start >= end) {return;}//找到要切割的位置int mid = (start + end) / 2;//左分支mergeSortFun(arr, start, mid);//右分支mergeSortFun(arr, mid + 1, end);//合并内容merge(arr, start, mid, end);}public static void merge(int[] arr, int left, int mid, int right) {//为了好理解,这里重新用s1,s2,e1,e2表示int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;//定义一个新的数组,用来返回排序好的部分int[] tmpArr = new int[right - left + 1];//用k表示下标(在新创建的数组中的位置)int k = 0;while(s1 <= e1 && s2 <= e2) {if(arr[s1] <= arr[s2]) {tmpArr[k++] = arr[s1++];} else {tmpArr[k++] = arr[s2++];}}//用来存放剩余的部分while(s1 <= e1) {tmpArr[k++] = arr[s1++];}while(s2 <= e2) {tmpArr[k++] = arr[s2++];}//将排序好的数组,放到原来的数组中for(int i = 0; i < tmpArr.length; i++) {arr[i + left] = tmpArr[i];}}public static void main(String[] args) {int[] arr = {10, 6, 7, 1, 3, 9, 4, 2};mergeSort(arr);for(int x : arr) {System.out.print(x + " ");}}
}
归并排序总结
1.归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题.
2.时间复杂度:O(N * logN)
3.空间复杂度:O(N)
4.稳定度:稳定.
海量数据的排序问题
外部排序:排序过程中需要在磁盘等外部存储进行的排序.
eg:内存只有1G,需要排序的数据有100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序.而归并排序是最常用的外部排序.
1.先把文件切分成200份,每个512M
2.分别对512M内容进行排序,因为每个内存都放得下,所以任意排序都可以
3.进行二路归并,同时对200份有序文件进行归并过程,最终结果就有序了.
自然归并排序
自然归并排序是归并排序的一种变体,其主要特点是利用输入数据的初始有序性.自然归并排序的思想是先找到已经有序的子序列,然后合并这些子序列,直至整个数组有序.
核心步骤讲解
1.查找有序子序列:从数组的起始位置开始,找到第一个有序子序列(递增或递减).这可以通过遍历数组来实现.
2.合并有序子序列:将找到的有序子序列进行合并,在合并的过程中,继续查找下一个有序子序列,直到整个数组有序.
3.重复步骤1和2:重复执行步骤1和2,直到整个数组完全有序.
以下是大致过程:

相对于之前的归并排序,这里就不是单纯的向下递归的过程,而是一个寻找子序列的过程,而在归并的过程中,是基本与之前的一致的.所以这里只需要分析一下寻找子序列的过程即可:
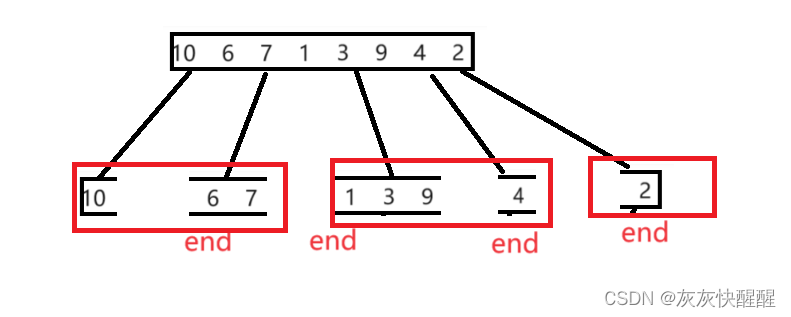
重点:标记的end是上一组的下一个,然后循环时不断标记end,控制为两两一组,进行合并.反复执行上述过程,就可以直接完成.
可能讲的会有点不清楚,请看代码:
import java.util.Arrays;public class NaturalMergeSort {public static void main(String[] args) {int[] array = {10, 6, 7, 1, 3, 9, 4, 2};naturalMergeSort(array);for(int x : array) {System.out.print(x + " ");}}public static void naturalMergeSort(int[] array) {int n = array.length;int[] tempArray = new int[n];int l = -1, m, r;//外部循环,直到不能发现更多的子数组while(l != 0) {l = 0;//内部循环,以寻找并合并有序子数组while (l < n) {m = findNextSortedSubarray(array, l, n, tempArray);//当m 与 n重合时,表明已经找到尾了,退出循环(里和外)if (m == n) {break;}r = findNextSortedSubarray(array, m, n, tempArray);merge(array, l, m, r, tempArray);l = r;}}}//查找下一个有序子数组的方法(返回的是结束位置)private static int findNextSortedSubarray(int[] array, int start, int n, int[] tempArray) {int end = start + 1;while (end < n && array[end - 1] <= array[end]) {end++;}return end;}//二路归并private static void merge(int[] array, int l, int m, int r, int[] tempArray) {int i = l, j = m, k = 0;while (i < m && j < r) {if (array[i] <= array[j]) {tempArray[k++] = array[i++];} else {tempArray[k++] = array[j++];}}while (i < m) {tempArray[k++] = array[i++];}while (j < r) {tempArray[k++] = array[j++];}System.arraycopy(tempArray, 0, array, l, k);}
}
自然归并排序总结
1.这玩意的思路相比于其它排序其实特别恶心,在生产环境中非常不建议使用,你的项目组成员可能会骂街,说你小子装什么逼??(除非是这种情况:就比如你的数据结构老师不知道是为啥心血来潮让你讲这个,整一个反转课堂啥的,那你也没办法~~)
2.时间复杂度:遍历了一次:O(n)
3.空间复杂度:O(n)