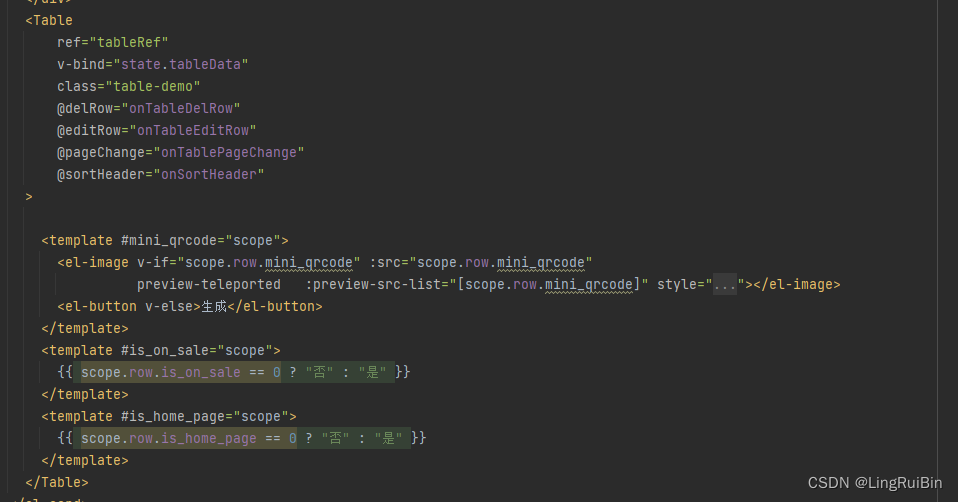
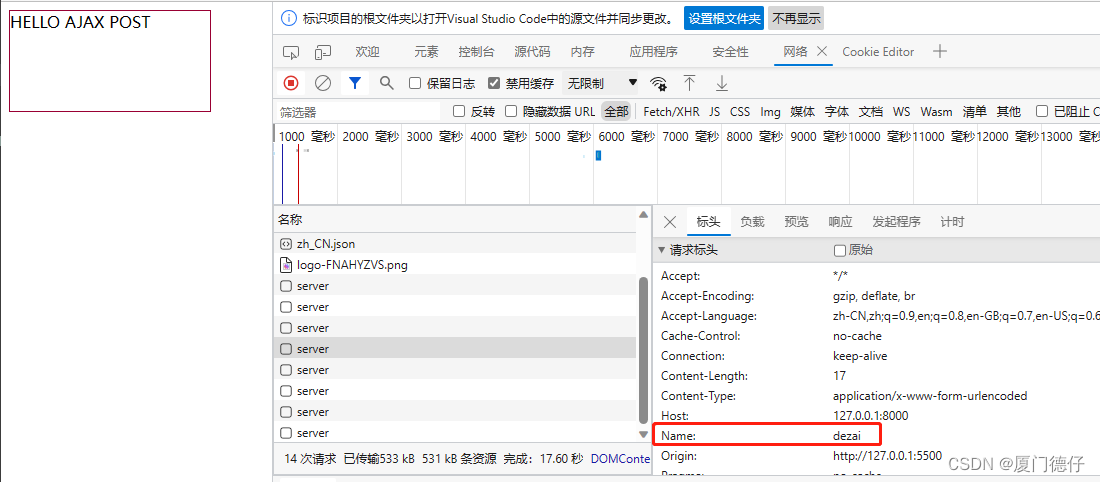
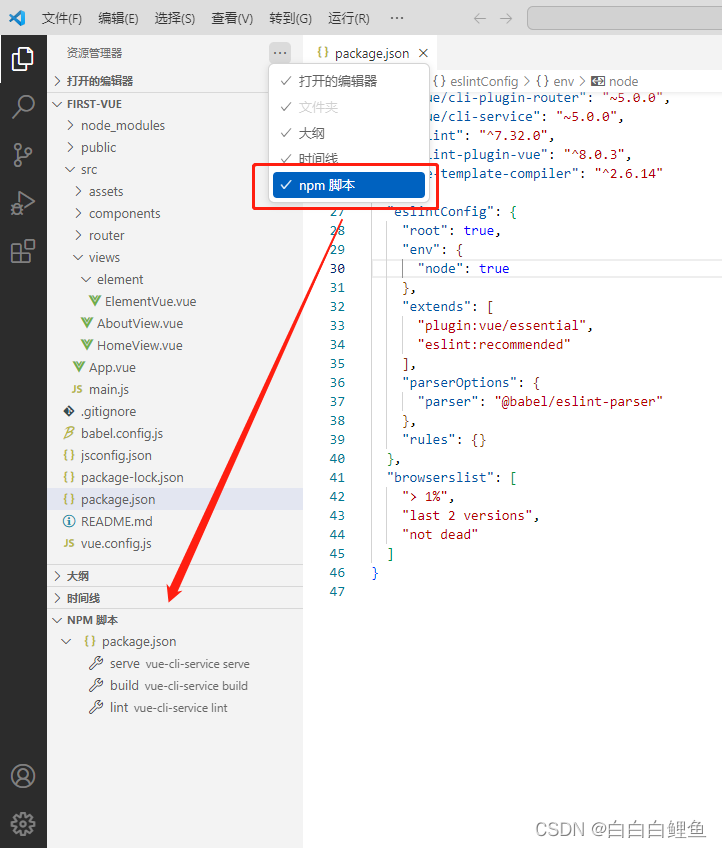
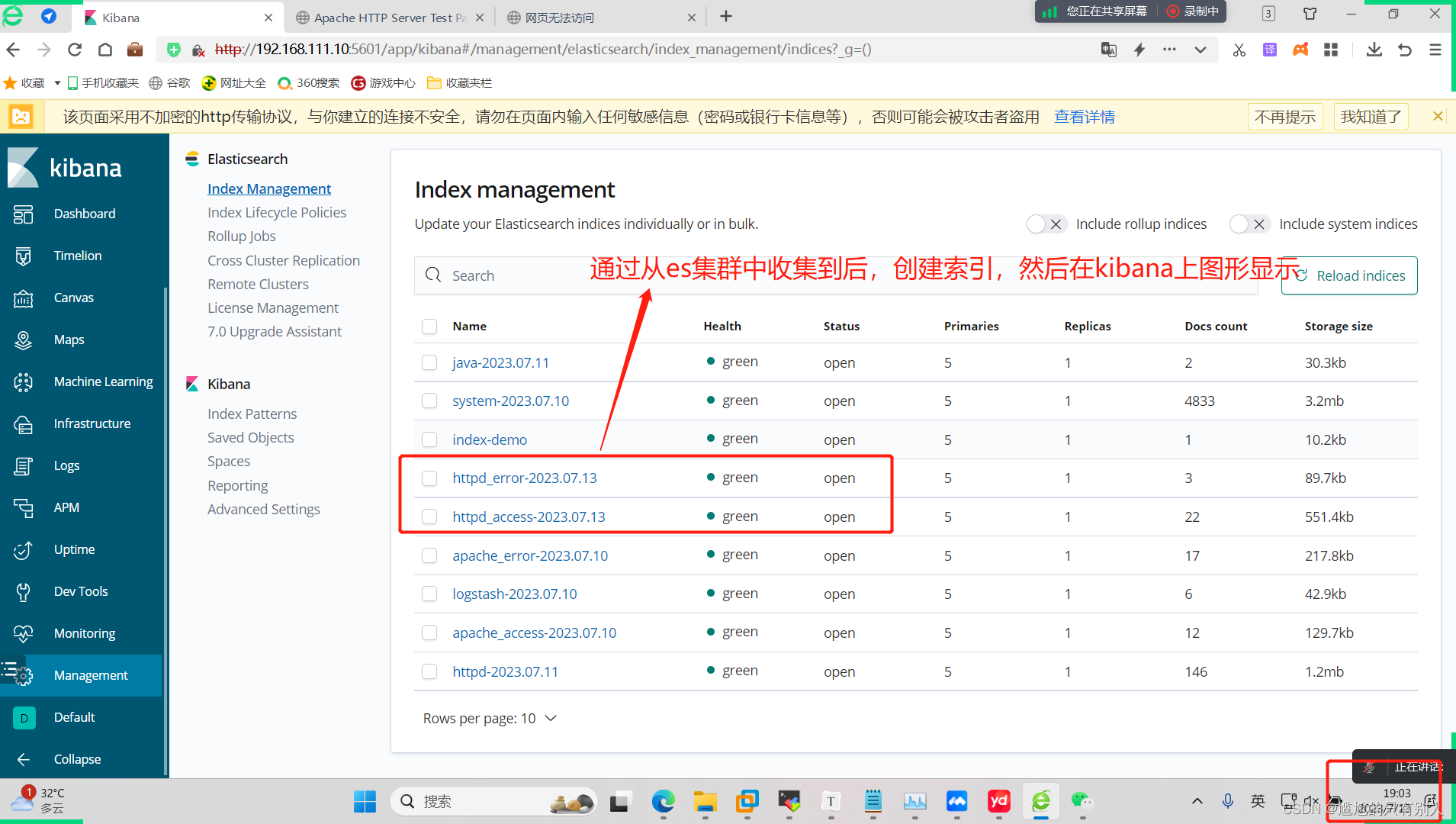
空间中的向量投影与最小二乘法
文章目录
- 空间中的向量投影与最小二乘法
- 一、引入
- 二、投影和投影的描述
- 1、投影描述最近
- 2、利用矩阵描述投影
- (1)向一维直线投影
- (2)向二维平面投影
- (3)向n维子空间投影的一般情况
- 三、最小二乘法
- 1、重要的子空间
- (1)互补的子空间
- (2)正交的子空间
- (3)相互正交补的子空间
- (4)投影过程中子空间的选择
- 2、最小二乘法
这一部分主要关于近似拟合
一、引入
- 线性方程无解情况:如何找到一个原始向量使得经过矩阵变换后距离目标向量最近
- 直线拟合:很多不在同一条直线上的点,如何找到一条直线距离这些点的距离最近
二、投影和投影的描述
1、投影描述最近
在空间中有一个穿过原点的直线,并且沿着向量 a a a的方向,在空间中有一个点 b b b,他不在直线上,如何在这条直线找到一个点,使之距离点 b b b最近?如图
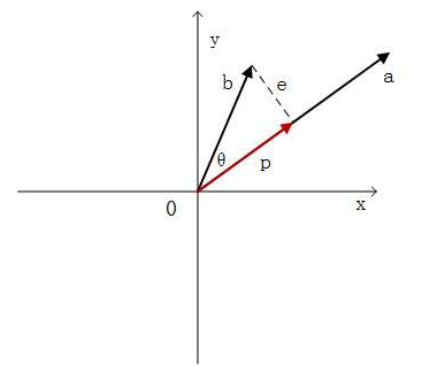
在图中,我们发现向量 b b b和向量 a a a的夹角是 θ \theta θ,因此通过b点到直线的最近距离是 ∣ b ∣ s i n θ |b| sin\theta ∣b∣sinθ。还需要注意到向量 p p p,从原点出发到垂直交点的向量,他是向量 b b b在向量 a a a上的投影。而向量 e = b − p e =b- p e=b−p我们称之为误差向量,他的长度就是我们要寻找的最近距离。
在二维、三维空间甚至是更高维空间中,需要使用矩阵工具来描述投影过程。
2、利用矩阵描述投影
如何用矩阵描述向量 b b b向一条直线、一个平面、一个 n n n维空间投影的过程呢?
(1)向一维直线投影

若向量 b b b向一条直线(以 a a a为基向量)投影,记为向量 p p p,向量 p p p可以用 a a a来表示, p = x ^ a p = \hat{x}a p=x^a( x ^ \hat{x} x^表示标量),我们最终可以通过求取这个 x ^ \hat{x} x^,最终得到投影 p p p和投影矩阵$P $.
核心:误差向量 e e e和基向量 a a a垂直,因此有 a ⋅ e = 0 a·e = 0 a⋅e=0,展开得 a ⋅ e = 0 → a ⋅ ( b − p ) = 0 → a ⋅ ( b − x ^ a ) = 0 a·e=0 \rightarrow a·(b - p) = 0 \rightarrow a·(b - \hat{x}a) = 0 a⋅e=0→a⋅(b−p)=0→a⋅(b−x^a)=0,此时便可得到 x ^ = a ⋅ b a ⋅ a \hat{x} = \frac{a·b}{a·a} x^=a⋅aa⋅b。由 a ⋅ b = a T b a·b = a^Tb a⋅b=aTb,最终得 x ^ = a T b a T a \hat{x} = \frac{a^Tb}{a^Ta} x^=aTaaTb.
因此我们可以得到 p = x ^ a = a T b a T a a p = \hat{x}a = \frac{a^Tb}{a^Ta}a p=x^a=aTaaTba
最后我们要得到将向量 b b b变换到其投影 p p p的变换矩阵 P P P,可以通过如下变换:
p = x ^ a = a T b a T a a = a a T b a T a = a a T a T a b p = \hat{x}a = \frac{a^Tb}{a^Ta}a = a \frac{a^Tb}{a^Ta} = \frac{aa^T}{a^Ta}b p=x^a=aTaaTba=aaTaaTb=aTaaaTb
由此可以得到投影矩阵 P = a a T a T a P = \frac{aa^T}{a^Ta} P=aTaaaT
(2)向二维平面投影
下面将问题拓展到二维平面,这个二维平面不仅局限于 R 2 R^2 R2平面,而是空间中任意过原点的二维平面,假设这个二维平面是 R m R^m Rm的子空间。
若向量中同样有一个向量 b b b,我们想在二维平面找到一个与之距离最近的向量,也就是找向量 b b b在平面上的投影向量 p p p,如图
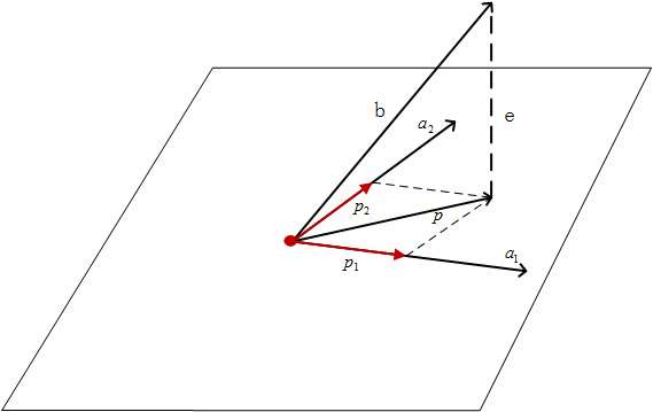
目标依旧是找到投影 p p p和投影矩阵 P P P.
上过高中的一般都知道,一条直线如果和一个平面垂直,则与平面所有向量垂直,选取二维平面两个线性无关的两个向量 a 1 , a 2 a_1,a_2 a1,a2作为平面的一组基。只要保证误差向量 e e e与 a 1 , a 2 a_1,a_2 a1,a2分别垂直,就能保证 e e e与整个平面垂直,向量 p p p就是向量 b b b在平面上的投影向量。
同样,核心:误差向量 e e e和基向量 a a a垂直。 a 1 ⋅ e = 0 a_1·e = 0 a1⋅e=0、 a 2 ⋅ e = 0 a_2·e = 0 a2⋅e=0,其中 e = b − p e = b - p e=b−p。
投影向量 p p p一定是 a 1 , a 2 a_1,a_2 a1,a2的线性组合,记作 p = p 1 + p 2 = x 1 ^ a 1 + x 2 ^ a 2 p = p_1 + p_2 = \hat{x_1}a_1 + \hat{x_2}a_2 p=p1+p2=x1^a1+x2^a2。将上面的式子进一步概括:记 A = [ a 1 , a 2 ] , x ^ = [ x 1 ^ x 2 ^ ] A = [a_1, a_2], \hat{x} = \left[\begin{matrix} \hat{x_1} \\\hat{x_2}\end{matrix} \right] A=[a1,a2],x^=[x1^x2^],可以将投影向量写为: p = A x ^ p = A\hat{x} p=Ax^.目标也就转换成求 x ^ \hat{x} x^了。
a 1 ⋅ e = 0 → a 1 ⋅ ( b − p ) = 0 → a 1 T ( b − A x ^ ) = 0 a_1·e = 0 \rightarrow a_1·(b - p) = 0\rightarrow a_1^T(b - A\hat{x}) = 0 a1⋅e=0→a1⋅(b−p)=0→a1T(b−Ax^)=0,同理 a 2 T ( b − A x ^ ) = 0 a_2^T(b - A\hat{x}) = 0 a2T(b−Ax^)=0,将两式结合 [ a 1 T a 2 T ] ( b − A x ^ ) = 0 \left[\begin{matrix} a_1^T\\a_2^T\end{matrix} \right](b - A\hat{x})=0 [a1Ta2T](b−Ax^)=0. A = [ a 1 , a 2 ] A = [a_1, a_2] A=[a1,a2],此时这个式子就是 A T ( b − A x ^ ) = 0 → A T A x ^ = A T b A^T(b - A\hat{x}) = 0 \rightarrow A^TA\hat{x} = A^Tb AT(b−Ax^)=0→ATAx^=ATb,最终有 x ^ = ( A T A ) − 1 A T b \hat{x} = (A^TA)^{-1}A^Tb x^=(ATA)−1ATb.
所以 p = A x ^ = A ( A T A ) − 1 A T b p = A\hat{x} = A(A^TA)^{-1}A^Tb p=Ax^=A(ATA)−1ATb,则投影矩阵 P = A ( A T A ) − 1 A T P = A(A^TA)^{-1}A^T P=A(ATA)−1AT.
(3)向n维子空间投影的一般情况
与二维类似。
x ^ = ( A T A ) − 1 A T b \hat{x} = (A^TA)^{-1}A^Tb x^=(ATA)−1ATb.
p = A x ^ = A ( A T A ) − 1 A T b p = A\hat{x} = A(A^TA)^{-1}A^Tb p=Ax^=A(ATA)−1ATb
P = A ( A T A ) − 1 A T P = A(A^TA)^{-1}A^T P=A(ATA)−1AT
以上讲解的便是如何将一个向量向空间中任意一个子空间进行投影的过程。
三、最小二乘法
最小二乘法关注的是向哪投影,即如何选择投影子空间的问题
1、重要的子空间
(1)互补的子空间
在一个 R m R^m Rm的空间中,我们可以选取 m m m个线性无关的向量 a 1 a_1 a1、 a 2 a_2 a2、…、 a m a_m am构成一组基,如果将这组基向量分为两个组,分别构成子空间,可以说这两个空间是互补关系。
概括的说,互补的子空间一方面由不同的基向量所张成,另一方面他们的维数之和为整个 R m R^m Rm空间的维数。空间任意一个向量向这些子空间上的投影之和,就是向整个空间的投影。
(2)正交的子空间
子空间 V V V和子空间 W W W正交成立的条件是,子空间 V V V中任意一个向量 v v v和子空间 W W W中任意一个向量 w w w都垂直。
(3)相互正交补的子空间
R m R^m Rm中的两个互补子空间,如果满足相互正交关系,则他们满足正交补的关系。
(4)投影过程中子空间的选择
前面我们提到,在子空间中寻找与目标向量 b b b最近的投影向量 p p p,前提就是误差向量 e = b − p e = b - p e=b−p与投影向量 p p p相互垂直。由于 b = e + p b = e + p b=e+p且 e ⋅ p = 0 e·p=0 e⋅p=0,则 p p p所在的子空间和 e e e所在的子空间在 R m R^m Rm中构成了正交补的关系。
对于一个 R m R^m Rm的空间,矩阵 A m n A_{mn} Amn,所有满足 A x = 0 Ax = 0 Ax=0的向量 x x x构成了 A A A的零空间 N ( A ) N(A) N(A),这个式子展开
A x = [ c o l 1 c o l 2 . . . c o l m ] x = [ 0 . . . 0 ] Ax = [col_1\ col_2\ ...\ col_m]x = \left[\begin{matrix} 0 \\...\\0\end{matrix} \right] Ax=[col1 col2 ... colm]x= 0...0 表明任意一个列向量与任意一个零向量垂直,因此列空间与零空间在 R m R^m Rm空间中满足正交互补。
2、最小二乘法
上面求取无解线性方程组近似解的方法就是最小二乘法。最终算得投影后的误差最小 ∣ e ∣ = ∣ b − p ∣ = ( b 1 − p 1 ) 2 + ( b 2 − p 2 ) 2 + . . . + ( b m − p m ) 2 |e| = |b - p| = \sqrt{(b_1 - p_1)^2+(b_2 - p_2)^2+...+(b_m - p_m)^2} ∣e∣=∣b−p∣=(b1−p1)2+(b2−p2)2+...+(bm−pm)2