给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
-
例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
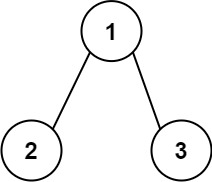
输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2 代表数字 12 从根到叶子节点路径 1->3 代表数字 13 因此,数字总和 = 12 + 13 = 25
示例 2:
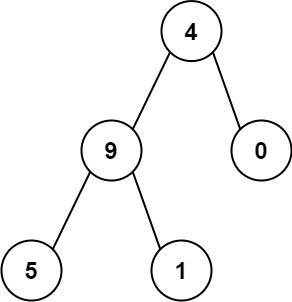
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495 从根到叶子节点路径 4->9->1 代表数字 491 从根到叶子节点路径 4->0 代表数字 40 因此,数字总和 = 495 + 491 + 40 = 1026
代码如下:
class Solution {
public:int dfs(TreeNode* root,int prevSum){if(root==nullptr){return 0;}int sum=prevSum*10+root->val;//当每遍历一个结点,更新一次sumif(root->left==nullptr&&root->right==nullptr)//当此节点为叶子节点(左右子树都为空)时,就返回sum,不再进行递归{return sum;}else{return dfs(root->left,sum)+dfs(root->right,sum);//递归的计算每一条路径上的值,调用dfs函数}}int sumNumbers(TreeNode* root) {return dfs(root,0);//返回dfs函数的最终结果,prevSum由0开始}
};