图形编辑器开发：一些会用到的简单几何算法-编程知识

图形编辑器开发：一些会用到的简单几何算法

大家好，我是前端西瓜哥。

开发图形编辑器，你会经常要解决一些算法问题。本文盘点一些我开发图形编辑器时遇到的简单几何算法问题。

矩形碰撞检测

判断两个矩形是否发生碰撞（或者说相交），即两个矩形有重合的区域。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cVfrKWlr-1689474500243)(https://fe-watermelon.oss-cn-shenzhen.aliyuncs.com/%E7%9F%A9%E5%BD%A2%E7%9B%B8%E4%BA%A4.gif)]

常见使用场景：

使用选择工具框选图形（框选策略除了相交，还可以用相交或其他方案）；
遍历图形，通过判断视口矩形和图形包围盒的矩形碰撞，剔除掉视口外的图形渲染操作，提高性能。

export function isRectIntersect2(rect1: IBox2, rect2: IBox2) {return (rect1.minX <= rect2.maxX &&rect1.maxX >= rect2.minX &&rect1.minY <= rect2.maxY &&rect1.maxY >= rect2.minY);
}

关于 IBox2 为包围盒的接口签名：

interface IBox2 {minX: number;minY: number;maxX: number;maxY: number;
}

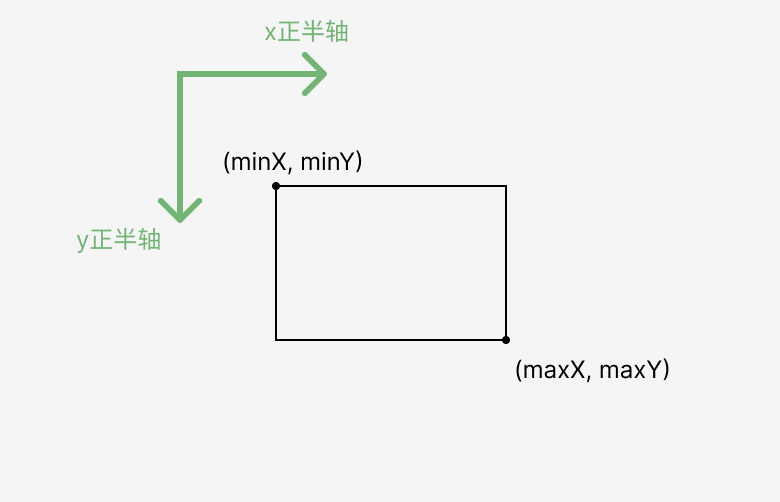
矩形包含检测

该算法用于判断矩形 1 是否包含矩形 2。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1iBS4e9A-1689474500244)(https://fe-watermelon.oss-cn-shenzhen.aliyuncs.com/%E7%9F%A9%E5%BD%A2%E5%8C%85%E5%90%AB.gif)]

常见使用场景：

使用选择工具框选图形（这次用的是包含策略）；

function isRectContain2(rect1: IBox2, rect2: IBox2) {return (rect1.minX <= rect2.minX &&rect1.minY <= rect2.minY &&rect1.maxX >= rect2.maxX &&rect1.maxY >= rect2.maxY);
}

计算旋转后坐标

对图形旋转，是一个非常基础的功能。计算旋转后的点是很常见的需求。

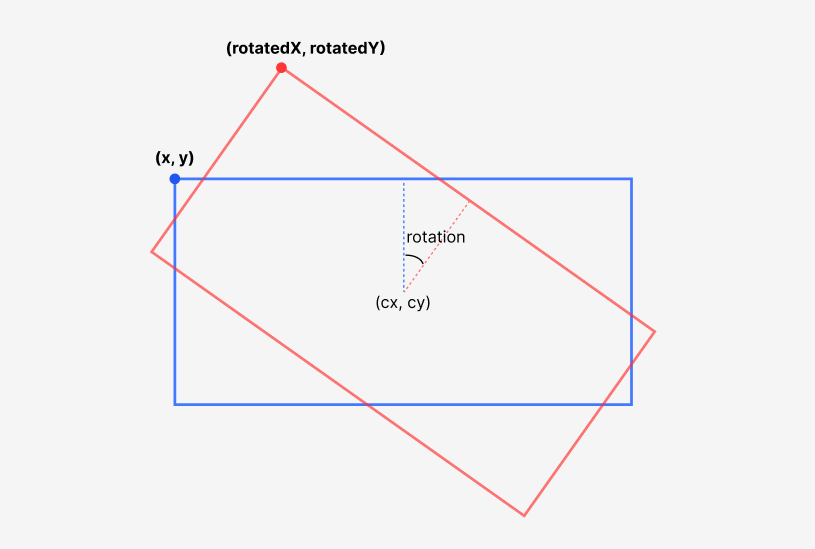
常见使用场景：

计算包围盒旋转后的坐标，绘制缩放控制点；
计算光标位置是否落在一个旋转的矩形上，因为旋转的矩形并不是一个正交的矩形，计算出来后判断有点复杂。所以通常我们会将光标给予矩形的中点反过来旋转一下，然后判断点是否在矩形中。

const transformRotate = (x: number,y: number,radian: number,cx: number,cy: number,
) => {if (!radian) {return { x, y };}const cos = Math.cos(radian);const sin = Math.sin(radian);return {x: (x - cx) * cos - (y - cy) * sin + cx,y: (x - cx) * sin + (y - cy) * cos + cy,};
}

点是否在矩形中

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UFGSUYIJ-1689474500245)(https://fe-watermelon.oss-cn-shenzhen.aliyuncs.com/%E9%80%89%E4%B8%AD.gif)]

常见使用场景：

用于实现图形拾取，判断矩形图形或包围盒是否在光标位置上。

function isPointInRect(point: IPoint, rect: IRect) {return (point.x >= rect.x &&point.y >= rect.y &&point.x <= rect.x + rect.width &&point.y <= rect.y + rect.height);
}

多个矩形组成的大矩形

选中多个矩形时，要计算它们组成的大矩形，然后绘制出大选中框。

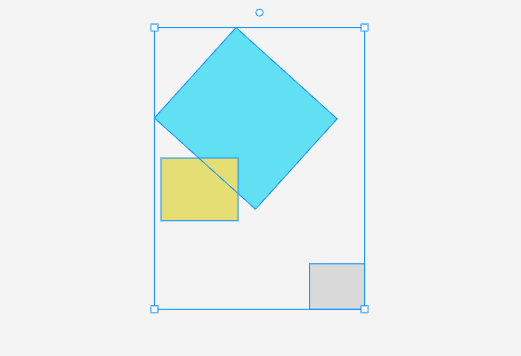
function getRectsBBox(...rects: IRect[]): IBox {if (rects.length === 0) {throw new Error('the count of rect can not be 0');}const minX = Math.min(...rects.map((rect) => rect.x));const minY = Math.min(...rects.map((rect) => rect.y));const maxX = Math.max(...rects.map((rect) => rect.x + rect.width));const maxY = Math.max(...rects.map((rect) => rect.y + rect.height));return {x: minX,y: minY,width: maxX - minX,height: maxY - minY,};
}

这里用的是另一种包围盒子的表达，所以多了一层转换。

interface IRect = {x: number;y: number;width: number;height: number;
}type IBox = IRect

计算向量夹角

通过旋转控制点旋转图形时，需要通过向量的点积公式来计算移动的夹角，去更新图形的旋转角度。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-I7Jpoyx9-1689474500245)(https://fe-watermelon.oss-cn-shenzhen.aliyuncs.com/%E6%97%8B%E8%BD%AC.gif)]

计算 [x - cx, y - cy] 和 [0, -1] 两个向量夹角的算法实现：

/*** 求向量到右侧轴(x正半轴)的夹角* 范围在 [0, Math.PI * 2)*/
export function calcVectorRadian(cx: number, cy: number, x: number, y: number) {const a = [x - cx, y - cy];const b = [0, -1];const dotProduct = a[0] * b[0] + a[1] * b[1];const d =Math.sqrt(a[0] * a[0] + a[1] * a[1]) * Math.sqrt(b[0] * b[0] + b[1] * b[1]);let radian = Math.acos(dotProduct / d);if (x < cx) {radian = Math.PI * 2 - radian;}return radian;
}