二叉树--基础OJ-编程知识

二叉树--基础OJ

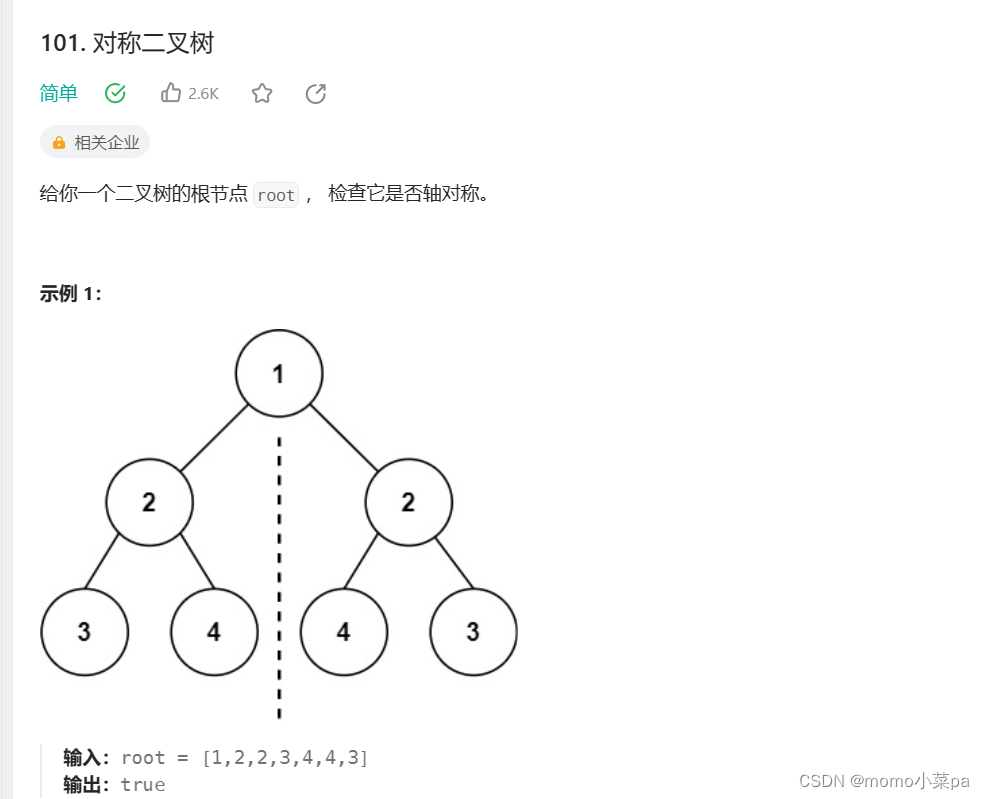
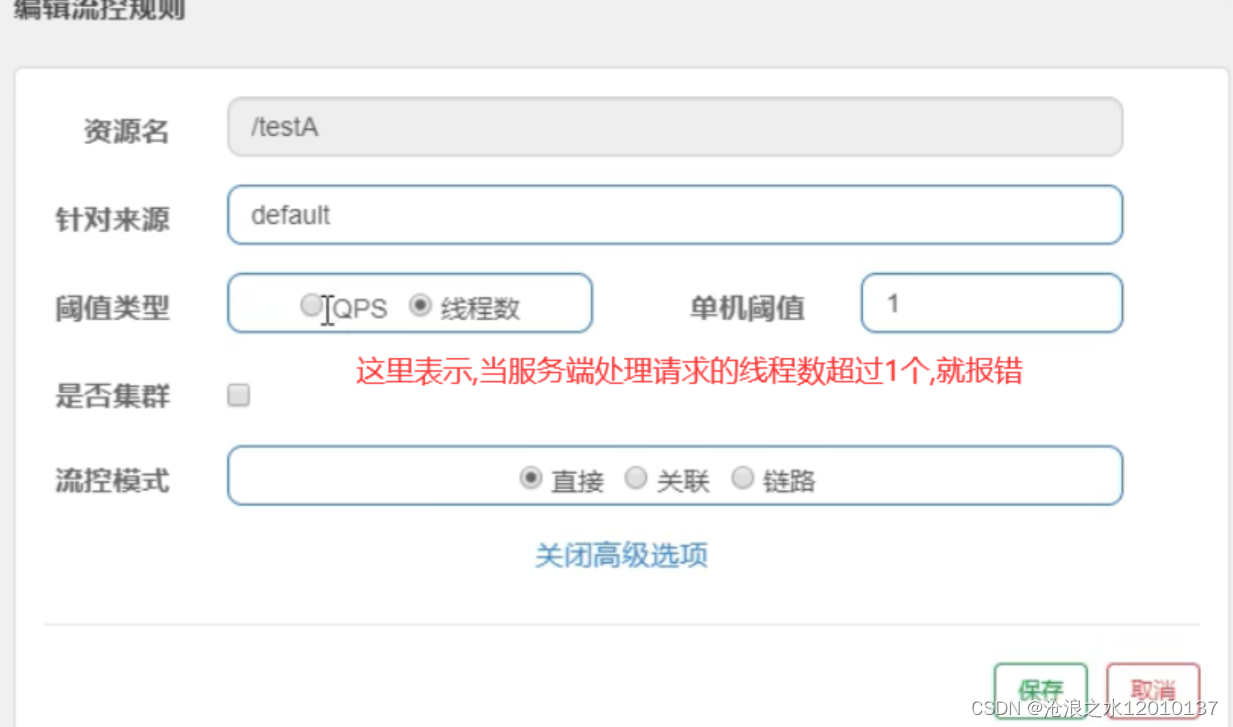
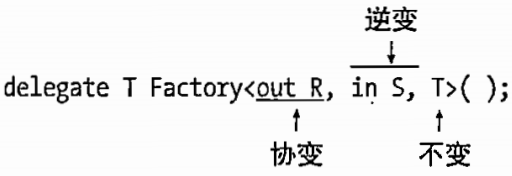
1.对称二叉树

题目链接：101. 对称二叉树 - 力扣（LeetCode）

题解：

我们可以用递归的方法去做：

如果两个树互为镜像（1.根节点的值相同，2.左子树的值与右子树的值对称）则为对称二叉树，我们先判断左右两棵树根节点的值，如果根节点的值相同，然后判断左右两棵树是否对称（左边树的左孩子是否等于右边树的右孩子，左边树的右孩子是否等于右边树的左孩子）我们依次递归，如果左右子树每个节点都满足以上两个条件，则为对称二叉树。

注意：需要对空进行判断，如果两边对称位置都出现空则不影响结果，如果两边对称位置一边为空，另一边非空，则不为对称二叉树

代码：
bool is(struct TreeNode* root1,struct TreeNode* root2)
{if(root1==NULL&&root2==NULL)return true;if(root1==NULL||root2==NULL)return false;if(root1->val != root2->val)return false;return is(root1->left,root2-> right)&&is(root1->right,root2->left);
}
bool isSymmetric(struct TreeNode* root) {return is(root->left,root->right);
}

2.翻转二叉树

题目链接：226. 翻转二叉树 - 力扣（LeetCode）

题解：

这一题其实就是上一题的变形，我们可以看到，翻转之后的图像和原来的图像是对称的关系，因此我们只需要和上一题一样，使用递归的操作依次对每个节点进行操作，我们需要让左右两颗子树的对称位置节点的值进行交换，这样就能变成原图像的对称图像。

代码：
void _invertTree(struct TreeNode* root){if(root){struct TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;_invertTree(root->left);_invertTree(root->right);}
}struct TreeNode* invertTree(struct TreeNode* root){_invertTree(root);return root;
}

3.平衡二叉树

题目链接：110. 平衡二叉树 - 力扣（LeetCode）

题解：

首先要保证当前树的左右子树高度差不大于1，而且子树本身也是平衡树。

这一题依然可以用递归的方法，分别检查左右子树，判断左右子树是否为平衡树，然后检查总体的。因此我们要分别求出左右子树的高度，判断两颗子树的高度差是否小于1（这里可以用到绝对值，左右子树都要进行这样的判断，因此递归条件可以写为：
fabs(TreeHeight(root->left)-TreeHeight(root->right))<=1&&isBalanced(root->left)&&isBalanced(root->right)
代码：
 int TreeHeight(struct TreeNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}
bool isBalanced(struct TreeNode* root) {if(root==NULL)return true;return fabs(TreeHeight(root->left)-TreeHeight(root->right))<=1&&isBalanced(root->left)&&isBalanced(root->right);
}

4.二叉树的前序遍历

题目链接：144. 二叉树的前序遍历 - 力扣（LeetCode）

题解：

要返回二叉树的前序遍历，那么我们使用二叉树前序遍历访问一个节点，就可以使用数组保存一个节点的值，我们通过题目接口可以看到，还要返回size，所有我们还要求二叉树节点的size。

是

代码：
void pre(struct TreeNode*root,int*a,int*i)
{if(root==NULL)return;a[(*i)++]=root->val;pre(root->left,a,i);pre(root->right,a,i);
}
int size(struct TreeNode*root)
{if(root==NULL){return 0;}return size(root->left)+size(root->right)+1;
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {int n = size(root);*returnSize =n;int*a=(int*)realloc(a,sizeof(int)*n);int i=0;pre(root,a,&i);return a;
}