参考
Reinforcement Learning, Second Edition
An Introduction
By Richard S. Sutton and Andrew G. Barto
强化学习与监督学习
强化学习与其他机器学习方法最大的不同,就在于前者的训练信号是用来评估(而不是指导)给定动作的好坏的。
强化学习:评估性反馈
有监督学习:指导性反馈
价值函数
最优价值函数,是给定动作 a a a 的期望,可以理解为理论最优
q ∗ ( a ) ≐ E [ R t ∣ A t = a ] q_*(a) \doteq\mathbb{E}[R_t|A_t=a] q∗(a)≐E[Rt∣At=a]
我们将算法对动作 a a a 在时刻 t t t 时的价值的估计记作 Q t ( a ) Q_t(a) Qt(a),我们希望它接近 q ∗ ( a ) q_*(a) q∗(a)
利用(Exploit)与探索(Explore)
利用:选择最高估计价值的动作(贪心)
探索:选择非贪心的动作
动作-价值方法(基于价值的方法)
思想:对价值进行估计,来选择动作。
采样平均方法
Q t ( a ) ≐ t 时刻前执行动作 a 得到的收益总和 t 时刻前执行动作 a 的次数 = ∑ i = 1 t − 1 R i 1 A i = a ∑ i = 1 t − 1 1 A i = a Q_t(a)\doteq \frac{t时刻前执行动作a得到的收益总和}{t时刻前执行动作a的次数}=\frac{\sum_{i=1}^{t-1} R_i \mathbf{1}_{A_i=a}}{\sum_{i=1}^{t-1} \mathbf{1}_{A_i=a}} Qt(a)≐t时刻前执行动作a的次数t时刻前执行动作a得到的收益总和=∑i=1t−11Ai=a∑i=1t−1Ri1Ai=a
贪心动作选择
最简单的动作选择规则是选择具有最高估计值的动作,即贪心动作
A t ≐ arg max a Q t ( a ) A_{t}\ \doteq \ {\arg \max_a}\ Q_{t}(a) At ≐ argamax Qt(a)
缺点:不能持续探索(虽然可以乐观初始化在开始阶段进行探索)
乐观初始化:对于纯粹贪心策略,可以把每一个初始值 Q 0 ( a ) Q_0(a) Q0(a)都设置得更大,从而鼓励算法在算法刚开始的时候尝试其他状态。因为一开始获得奖励之后都把 Q 0 ( a ) Q_0(a) Q0(a)降低了。
ϵ \epsilon ϵ-贪心方法
以小概率 ϵ \epsilon ϵ随机选择动作, 1 − ϵ 1-\epsilon 1−ϵ 贪心选择
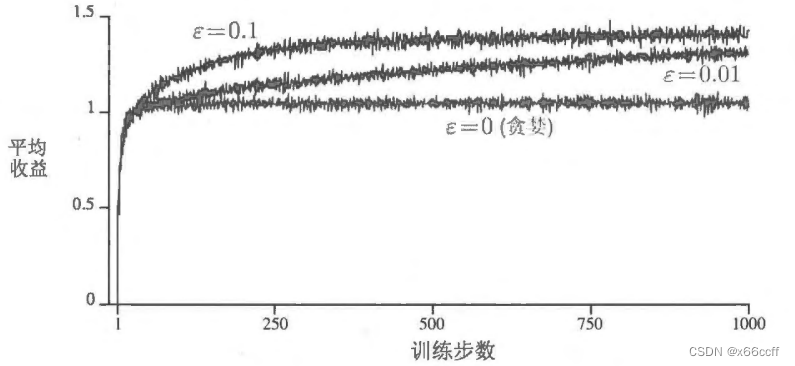

两者都并不是完美的
贪心动作虽然在当前时刻看起来最好,但实际上其他一些动作可能从长远看更好
ϵ \epsilon ϵ-贪心算法会尝试选择非贪心的动作,但是这是一种盲目的选择,因为它不大会去选择接近贪心或者不确定性特别大的动作
增量更新、平稳/非平稳问题
为了计算效率,采用增量更新:
Q n + 1 = Q n + 1 n [ R n − Q n ] Q_{n+1} = Q_n + \frac{1}{n}[R_n - Q_n ] Qn+1=Qn+n1[Rn−Qn]
此时 α = 1 n \alpha = \frac{1}{n} α=n1,适合平稳分布的问题,但是如果 bandit 背后的分布是会变化的,那么 α \alpha α 应该采用 > 1 n >\frac{1}{n} >n1 ,从而给更靠近的奖励更大的权重。
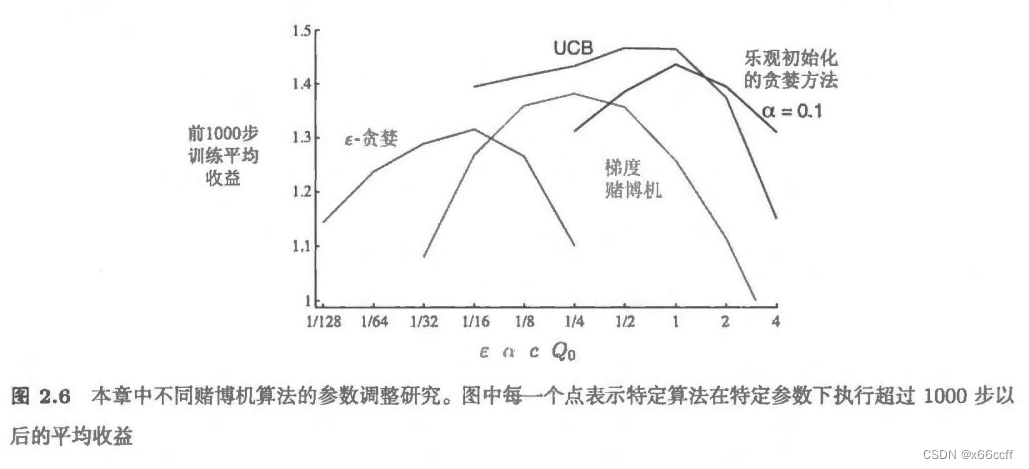
UCB
置信度上界 (upper confidence bound, UCB)——平衡了 探索与利用
A t ≐ a r g max a [ Q t ( a ) + c ln t N t ( a ) ] A_{t}\ \doteq \ {\mathrm{arg}}\max_a\left[Q_{t}(a)+c\sqrt{\frac{\ln t}{N_{t}(a)}}\,\right] At ≐ argamax[Qt(a)+cNt(a)lnt]
左边:利用平均奖励大的动作
右边:鼓励探索访问次数少的动作,但是同时要考虑到其他非 a a a 的状态的访问次数,用 t t t近似。每次选 a a a之外的动作时,在分子上的 ln t \ln t lnt增大,而 N t ( a ) N_t(a) Nt(a) 却没有变化,所以不确定性增加了
UCB一般来说比贪心、 ϵ \epsilon ϵ-贪心 要好。
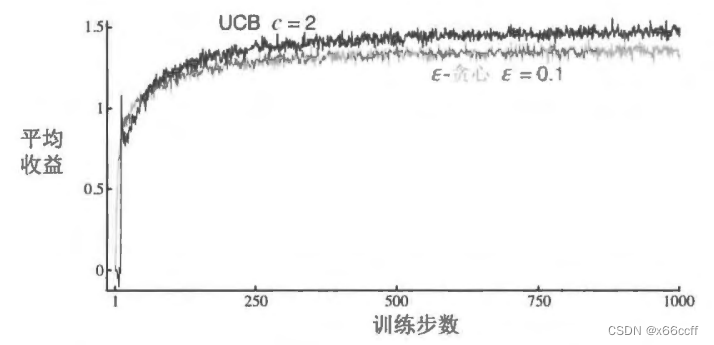
UCB 的缺点:
- 处理非平稳问题时,需要一些更复杂的 tricks, 不能仅仅使用这样的策略。
- 处理不了很大的状态空间。
上下文赌博机(Contextual Bandit)
普通的赌博机:算法每一次选择新动作的时候,没有额外的环境信息。
上下文赌博机:算法每一次选择新动作的时候,有额外的环境信息。
也许你面对的是一个真正的老虎机、它的外观颜色与它的动作价值集合一一对应,动作价值集合改变的时候,外观颜色也会改变.那么,现在你可以学习一些任务相关的操作策略,例如,用你所看到的颜色作
为信号,把每个任务和该任务下最优的动作直接关联起来,比如,如果为红色, 则选择1号臂 ;如果为绿色,则选择2号臂。有了这种任务相关的策略,在知道任务编号信息时,你通常要比不知道任务编号信息时做得更好。
——《RL》
上下文赌博机介于多臂赌博机问题和完整强化学习问题之间。它与完整强化学习问题的相似点是,它需要学习一种策略,但它又与多臂赌博机问题相似,体现在每个动作只影响即时收益。
总结
在多臂赌博机问题来说,一般来说,UCB是比贪心, ϵ \epsilon ϵ-贪心更好的