1-什么是跳表
跳表SkipList是一种随机化的数据结构,基于并联的链表,实现简单,插入、删除、查找的复杂度均为 O(logN)(大多数情况下,因为是实现上是概率问题),因为其性能匹敌红黑树且实现较为简单,因此在很多著名项目都用 SkipList 来代替红黑树,例如Redis中的有序集合zset 的底层存储结构就是用的skiplist。
跳跃列表由 William Pugh 发明。他在 Communications of the ACM发表了《Skip lists: a probabilistic alternative to balanced trees》,在其中详细描述了他的工作。
假设原始链表的数据如下:链表中存储的数据是有序的。

我们知道这种链表结构查询数据的时间复杂度是O(n)。但是如果我们对链表建立"索引",把节点数据提取出来放在上一级(索引层),这样是不是就可以提高查询效率了呢?比如我们查找元素83;如果按照原始链表,要查询8个节点,采用下面这个结构,只需要查询5个节点。如果数据量越大,优势就更加明显。

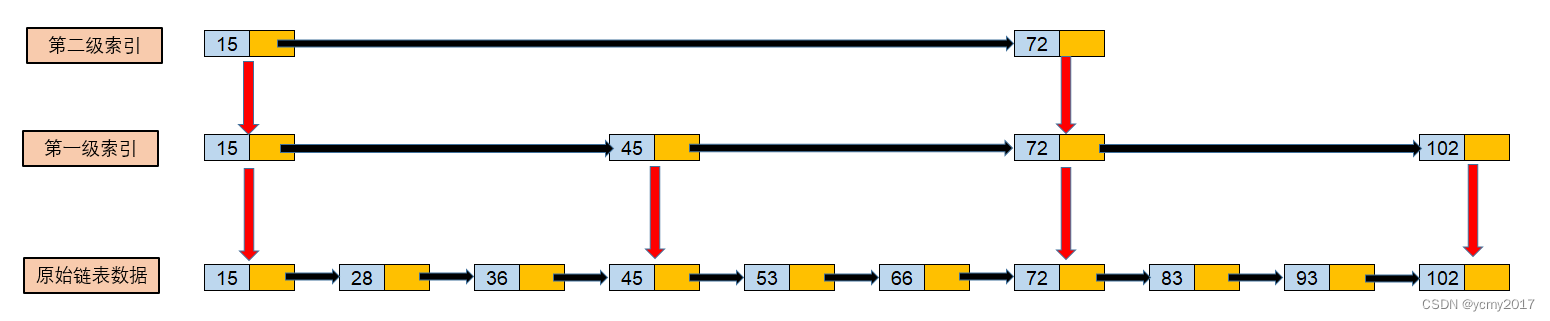
这种链表加多级索引的结构,就是跳表。
2-跳表的查询
我们知道,在一个单链表中查询某个数据的时间复杂度是O(n)。那么跳表的时间复杂度是多少呢?
假设每两个结点会抽出一个结点作为上一级索引的结点,那第一级索引的结点个数大约就是n/2,第二级索引的结点个数大约就是n/4,第三级索引的结点个数大约就是n/8,依次类推,也就是说,第k级索引的结点个数是第k-1级索引的结点个数的1/2,那第k级索引结点的个数就是n/(2^k)。
假设最高级索引有两个节点,最高级索引是k,总节点数是n,那么n/(2^k)=2,k=logn -1(以2为底的对数)。如果包含原始链表这一层,整个跳表的高度就是logn。我们在跳表中查询某个数据的时候,如果每一层都要遍历m个结点,那在跳表中查询一个数据的时间复杂度就是O(m*logn)。一般m是常数,所以在跳表中查询任意数据的时间复杂度就是O(logn)。这个时间复杂度是不是跟二分查找一样,很高效了。但是这种效率的提升,是以空间换时间的理念来实现的。
假设我们每两个节点抽取一个,需要多使用n/2+n/4+n/8…+8+4+2=n-2。跳表的空间复杂度是O(n)。也就是说,如果将包含n个结点的单链表构造成跳表,我们需要额外再用接近n个结点的存储空间。假设我们每3个节点抽取一个,总的索引结点大约就是n/3+n/9+n/27+…+9+3+1=n/2,空间复杂度还是O(n),但比上面的每两个结点抽一个结点的索引构建方法,要减少了一半的索引结点存储空间。
其实我们不必太在意索引占用的额外空间,因为实际的软件开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
3-跳表的插入-删除-索引的动态更新
插入:在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是O(1)。但是,这里为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找操作就会比较耗时O(n)。但是,对于跳表来说,我们讲过查找某个结点的的时间复杂度是O(logn),所以这里查找某个数据应该插入的位置,方法也是类似的,时间复杂度也是O(logn)。
删除:如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。
索引动态更新:当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某2个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入、删除操作性能下降。
当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢?我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值K,那我们就将这个结点添加到第一级到第K级这K级索引中。随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
4-redis跳表使用
Redis中的有序集合zset 的底层存储结构就是用的skiplist,为何不使用红黑树等平衡树?主要原因有以下几点:
1-高效的查找操作:跳表通过建立多层索引,可以在有序集合中实现快速的查找操作。相比于传统的平衡树结构(如红黑树),跳表的查找操作具有更低的时间复杂度,平均情况下为O(log n)。
2-简单且易于实现:相对于其他复杂的数据结构(如红黑树或AVL树),跳表的实现相对简单且容易理解。它没有复杂的平衡调整操作,只需通过维护索引层来保持有序性和高效性。
3-空间效率较高:跳表通过层级结构来建立索引,每个节点只需额外存储少量的指针信息。相比于一些平衡树结构,跳表在空间使用上通常更加高效。
还有一个业务功能原因:对于按照区间查找数据ZRANGE这个操作,跳表可以做到O(logn)的时间复杂度定位区间的起点,然后在原始链表中顺序往后遍历就可以了。这样做非常高效。