从源码理解Scala中函数reduceRight的计算过程-编程知识

从源码理解Scala中函数reduceRight的计算过程

水善利万物而不争，处众人之所恶，故几于道💦

以List集合为例，进行reduceRight()的计算过程分析，总体分为两部分，一部分是看最顶层特质的那个通用的reduceRight方法，另一部分是讲直接混入的特质的那个重写的reduceRight方法，两种方式最终结果一致。

例如：

val list2: List[Int] = List(3, 4, 5, 8, 10)
println(list2.reduceRight(_ - _))   // 6

上面的这两行代码输出的结果是6
接下来我们从源码的角度刨析一下这个结果是怎么算出来的

首先我们点进list的reduce里面，查看他的源代码

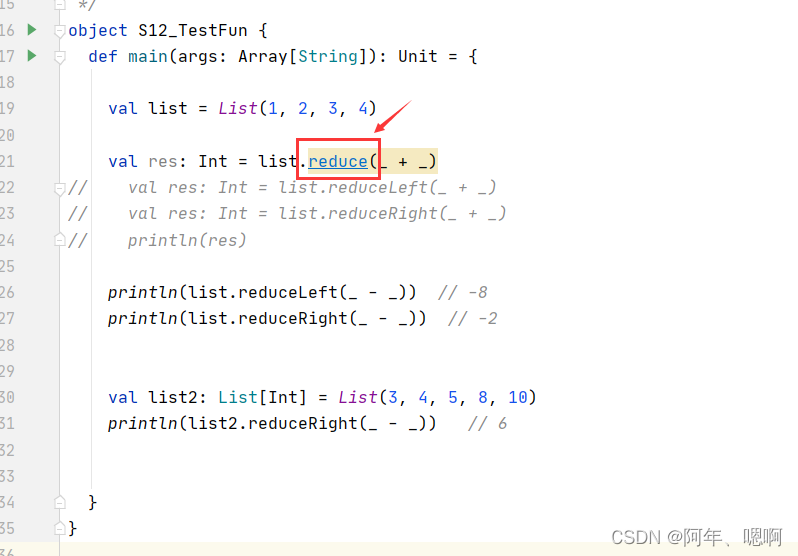
在这里插入图片描述

点进去后在这个特质里面找到reduceRight方法
这个方法它首先是判断了一下方法调用这也就是哪个集合是否为空，如果为空，直接抛异常。
其次他就开始进行reduceRight的操作。看代码，他的操作是：将集合反转，然后调用reduceLeft方法，这个op就是我们的_-_操作，也就是简化/规约的逻辑。它具体执行的时候将传入的两个参数进行了位置调换。

在这里插入图片描述

举例来说：List(3, 4, 5, 8, 10).reduceRight(_ - _)

1. 它先把集合反转得到List(10, 8, 5, 4, 3).reduceLeft(_ - _)

2. 然后在进行相减操作的时候，传入的参数本来是（x，y）也就是x=10，y=8 但是它方法体中调用的时候是op(y, x)也就是op(8, 10)

3. 带入到我们的例子中就是：8-10，然后 5-(8-10) ，4-(5-(8-10)) ， 3-(4-(5-(8-10)))。算出最总结果是6

刚才那个reduceRight是最顶层特质的方法实现，也最容易看懂。所以先把那个最容易的看懂。

下面这个是真正执行的时候走的方法。

在这里插入图片描述

这两个特质是父子关系，LinearSeqOptimized特质是TraversableOnce特质的子特质，

TraversableOnce特质里面的reduceRight方法实现就是：

def reduceRight[B >: A](op: (A, B) => B): B = {if (isEmpty)throw new UnsupportedOperationException("empty.reduceRight")reversed.reduceLeft[B]((x, y) => op(y, x))
}

实际上走的LinearSeqOptimized特质里面的reduceRight方法其实是对父特质里面reduceRight方法的重写。

在这里插入图片描述

查看TraversableOnce特质的层次结构，看到LinearSeqOptimized特质是它的子特质。

在这里插入图片描述

实际上走的是这段代码：

override /*IterableLike*/
def reduceRight[B >: A](op: (A, B) => B): B =if (isEmpty) throw new UnsupportedOperationException("Nil.reduceRight")else if (tail.isEmpty) headelse op(head, tail.reduceRight(op))

1. 首先它判断了一下集合是否为空，空的话直接抛异常

2. 否则判断集合的尾是否为空，如果为空的话直接将头部返回。意思就是，如果集合中只有一个元素的话，直接将该元素返回。

3. 接下来进行我们的简化/规约操作，op是我们传过来的函数，也就是(a:Int,b:Int)=>{a-b}。op的第一个参数是集合的头，也就是3，第二个参数是尾再进行reduceRight(op)操作，可以看到有递归调用，所以第一次执行后的结果是：

3 - List(4,5,8,10).reduceRight(_-_)  // 第一次执行然后递归调用，第二次执行...3 - (4 - List(5,8,10).reduceRight(_-_)) // 第二次递归调用3 - (4 - (5 - List(8,10).reduceRight(_-_)))  //第三次递归调用3 - (4 - (5 - (8 - List(10).reduceRight(_-_))))  //第四次递归调用第五次递归调用的时候，由于集合中只有一个元素，
在进行 else if 条件判断的时候，返回 10 ，也就是到了递归出口3 - (4 - (5 - (8 - 10)))  //第五次递归调用