NNDL 作业10 BPTT-编程知识

习题6-1P 推导RNN反向传播算法BPTT.

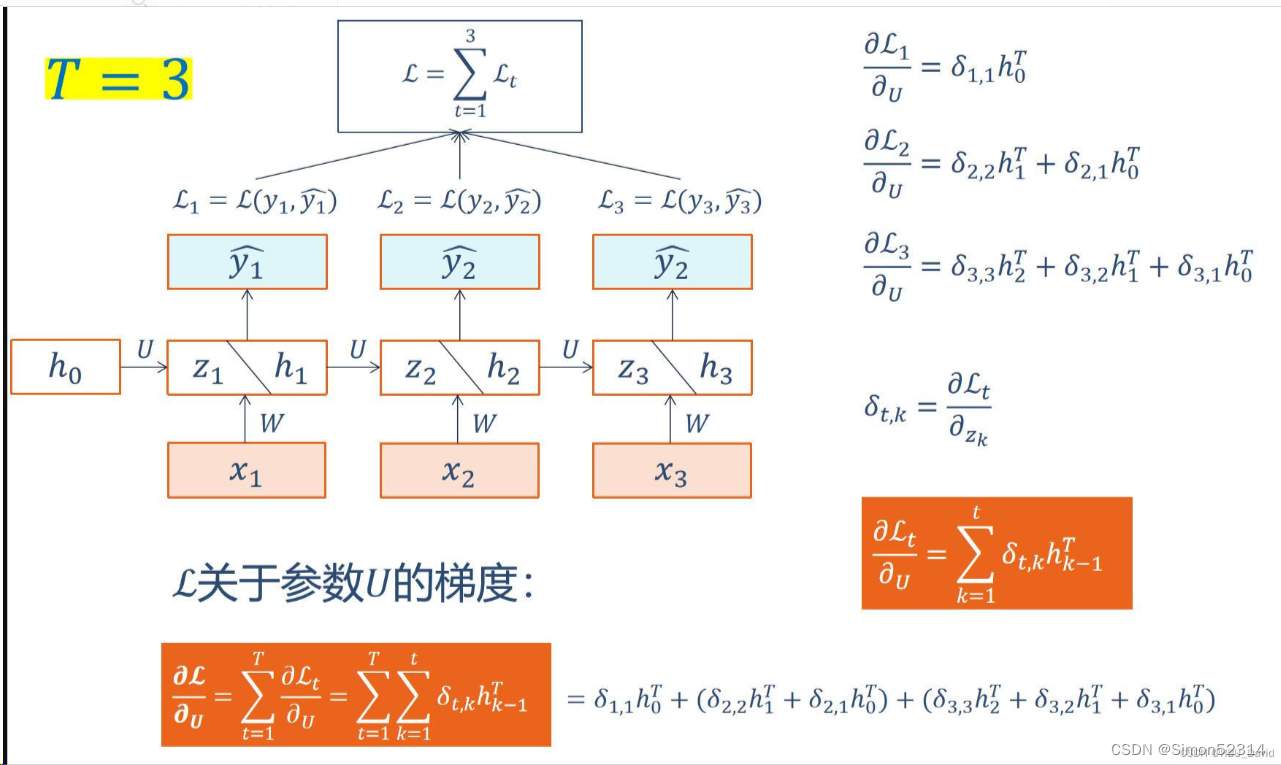
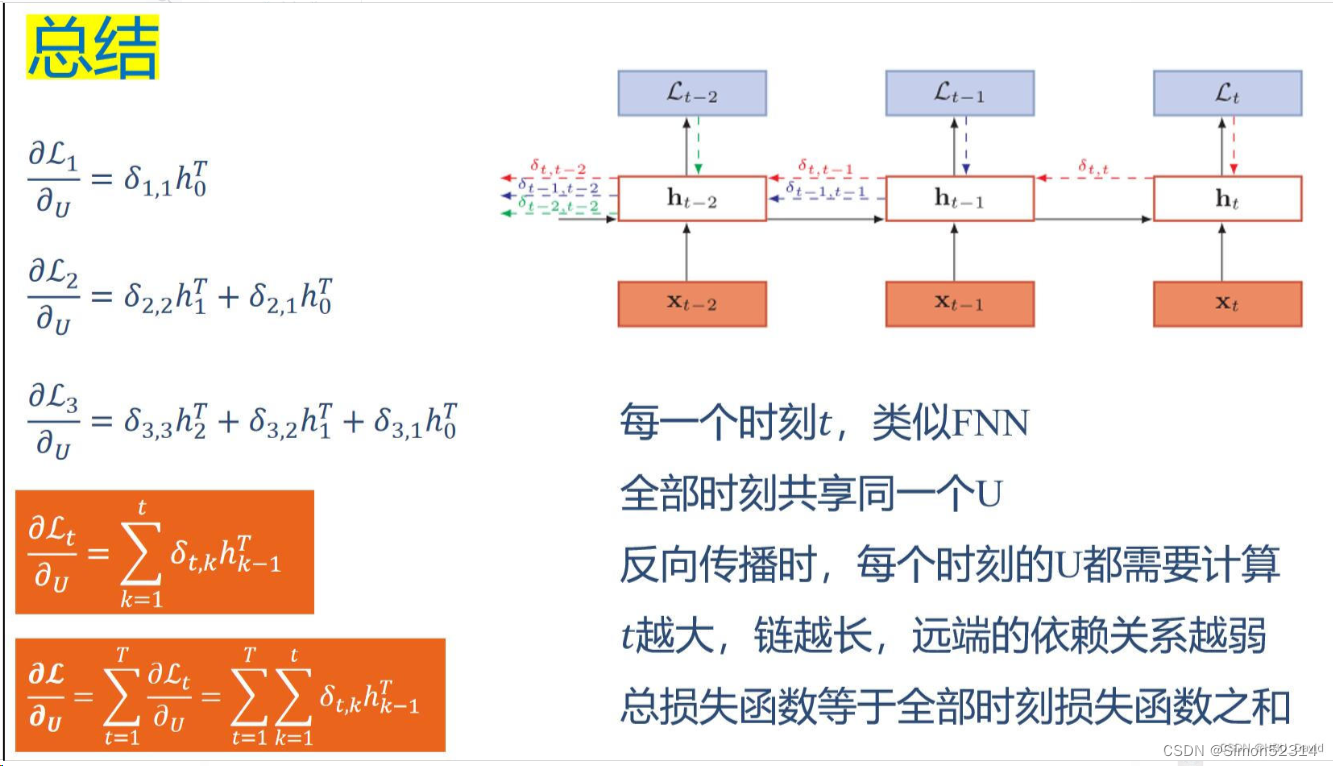
我的推导

和PPT结果对比，可得答案没问题

习题6-2 推导公式(6.40)和公式(6.41)中的梯度．

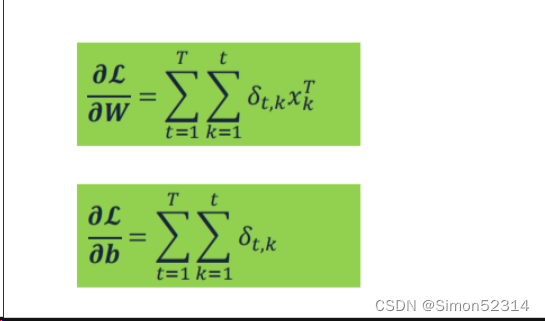
习题6-3 当使用公式(6.50)作为循环神经网络的状态更新公式时，分析其可能存在梯度爆炸的原因并给出解决方法．

解决方法．

梯度消失

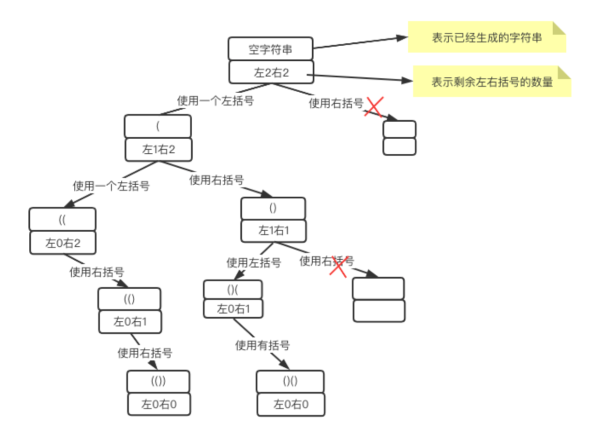
挺好奇门控循环单元的，就看到我室友呕心沥血的巨作，我拜读一下，大呼牛逼！

门控机制的核心思想是通过一些门控单元，来控制信息的流动和保存。这些门控单元充当了数据的筛选器，可以选择性地让某些信息通过或阻止。主要的门控单元有以下两种：

遗忘门（Forget Gate）：
- 在LSTM中存在遗忘门，它决定了前一时刻的记忆状态中哪些信息需要被保留，哪些需要被遗忘。
- 遗忘门的输出是一个在0到1之间的值，用于加权前一时刻的记忆状态。
输入门（Input Gate）：
- 输入门决定了当前时刻的输入信息中哪些部分需要被添加到记忆状态中。
- 输入门的输出是一个在0到1之间的值，表示对应位置的输入是否重要。

这两个门控单元使得LSTM网络能够更好地处理长序列信息，允许网络选择性地记住和遗忘信息。

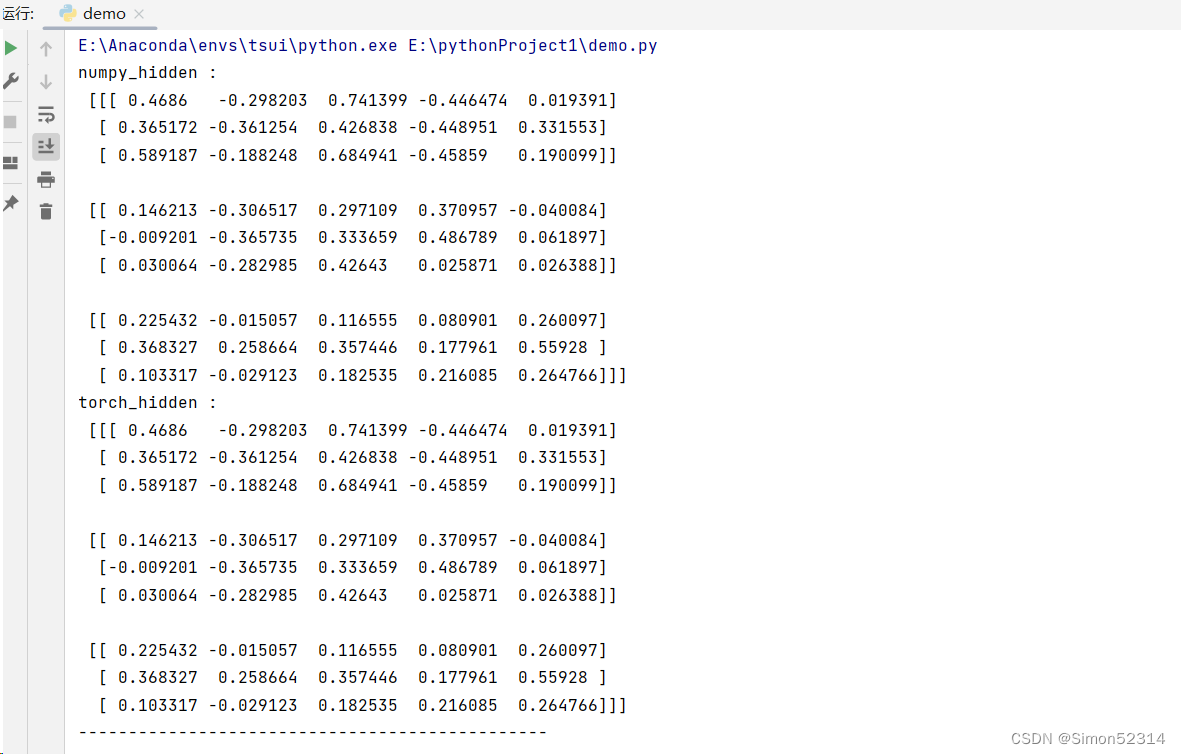
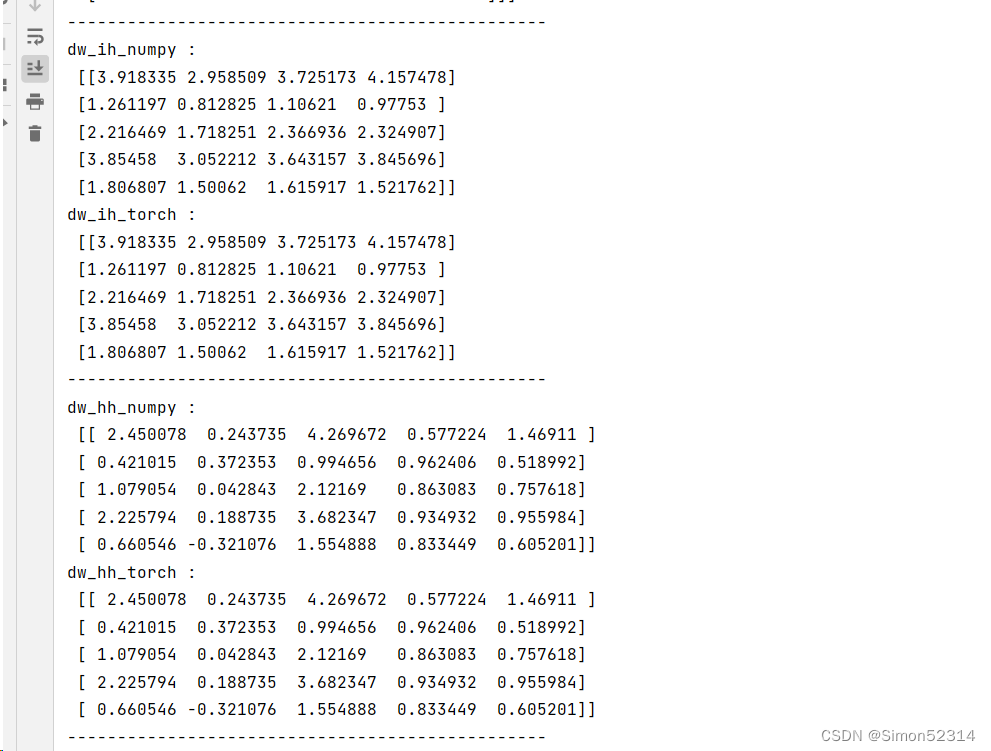
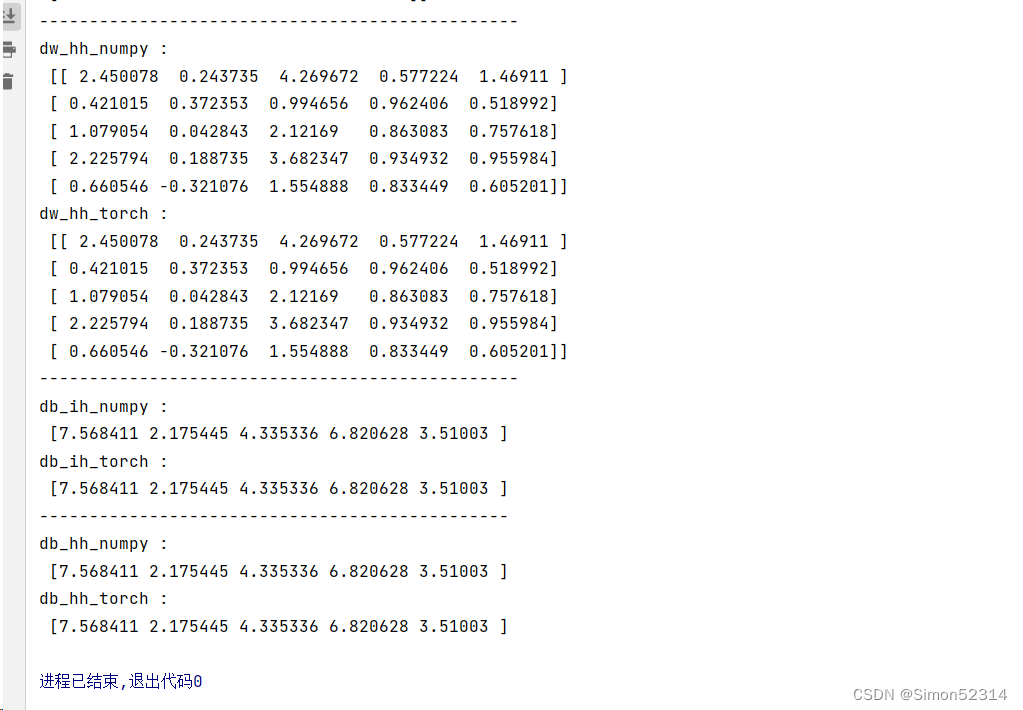
习题6-2P 设计简单RNN模型，分别用Numpy、Pytorch实现反向传播算子，并代入数值测试.

import torch
import numpy as np
class RNNCell:def __init__(self, weight_ih, weight_hh, bias_ih, bias_hh):self.weight_ih = weight_ihself.weight_hh = weight_hhself.bias_ih = bias_ihself.bias_hh = bias_hhself.x_stack = []  # 存储输入样本self.dx_list = []  # 存储反向传播计算得到的输入梯度self.dw_ih_stack = []  # 存储反向传播计算得到的输入权重梯度self.dw_hh_stack = []  # 存储反向传播计算得到的隐藏层权重梯度self.db_ih_stack = []  # 存储反向传播计算得到的输入偏置梯度self.db_hh_stack = []  # 存储反向传播计算得到的隐藏层偏置梯度self.prev_hidden_stack = []  # 存储前一时刻的隐藏状态self.next_hidden_stack = []  # 存储当前时刻的隐藏状态self.prev_dh = None  # 临时缓存，用于存储前一时刻的隐藏状态梯度def __call__(self, x, prev_hidden):self.x_stack.append(x)next_h = np.tanh(np.dot(x, self.weight_ih.T)+ np.dot(prev_hidden, self.weight_hh.T)+ self.bias_ih + self.bias_hh)  # 前向传播计算隐藏状态self.prev_hidden_stack.append(prev_hidden)self.next_hidden_stack.append(next_h)self.prev_dh = np.zeros(next_h.shape)  # 清空隐藏状态梯度缓存return next_hdef backward(self, dh):x = self.x_stack.pop()prev_hidden = self.prev_hidden_stack.pop()next_hidden = self.next_hidden_stack.pop()d_tanh = (dh + self.prev_dh) * (1 - next_hidden ** 2)  # 计算当前时刻的隐藏状态梯度self.prev_dh = np.dot(d_tanh, self.weight_hh)  # 更新前一时刻隐藏状态梯度缓存dx = np.dot(d_tanh, self.weight_ih)  # 计算输入梯度self.dx_list.insert(0, dx)dw_ih = np.dot(d_tanh.T, x)  # 计算输入权重梯度self.dw_ih_stack.append(dw_ih)dw_hh = np.dot(d_tanh.T, prev_hidden)  # 计算隐藏层权重梯度self.dw_hh_stack.append(dw_hh)self.db_ih_stack.append(d_tanh)  # 存储输入偏置梯度self.db_hh_stack.append(d_tanh)  # 存储隐藏层偏置梯度return self.dx_listif __name__ == '__main__':np.random.seed(123)torch.random.manual_seed(123)np.set_printoptions(precision=6, suppress=True)# 创建一个PyTorch的RNN模型rnn_PyTorch = torch.nn.RNN(4, 5).double()# 使用PyTorch参数初始化一个对应的NumPy RNN模型rnn_numpy = RNNCell(rnn_PyTorch.all_weights[0][0].data.numpy(),rnn_PyTorch.all_weights[0][1].data.numpy(),rnn_PyTorch.all_weights[0][2].data.numpy(),rnn_PyTorch.all_weights[0][3].data.numpy())nums = 3x3_numpy = np.random.random((nums, 3, 4))  # 随机生成输入样本x3_tensor = torch.tensor(x3_numpy, requires_grad=True)h3_numpy = np.random.random((1, 3, 5))  # 随机生成初始隐藏状态h3_tensor = torch.tensor(h3_numpy, requires_grad=True)dh_numpy = np.random.random((nums, 3, 5))  # 随机生成隐藏状态梯度dh_tensor = torch.tensor(dh_numpy, requires_grad=True)h3_tensor = rnn_PyTorch(x3_tensor, h3_tensor)  # PyTorch前向传播h_numpy_list = []h_numpy = h3_numpy[0]for i in range(nums):h_numpy = rnn_numpy(x3_numpy[i], h_numpy)  # NumPy前向传播h_numpy_list.append(h_numpy)h3_tensor[0].backward(dh_tensor)  # PyTorch反向传播for i in reversed(range(nums)):rnn_numpy.backward(dh_numpy[i])  # NumPy反向传播# 打印NumPy和PyTorch的输出结果进行对比print("numpy_hidden :\n", np.array(h_numpy_list))print("torch_hidden :\n", h3_tensor[0].data.numpy())print("-----------------------------------------------")# 打印NumPy和PyTorch的输入梯度进行对比print("dx_numpy :\n", np.array(rnn_numpy.dx_list))print("dx_torch :\n", x3_tensor.grad.data.numpy())print("------------------------------------------------")# 打印NumPy和PyTorch的输入权重梯度进行对比print("dw_ih_numpy :\n",np.sum(rnn_numpy.dw_ih_stack, axis=0))print("dw_ih_torch :\n",rnn_PyTorch.all_weights[0][0].grad.data.numpy())print("------------------------------------------------")# 打印NumPy和PyTorch的隐藏层权重梯度进行对比print("dw_hh_numpy :\n",np.sum(rnn_numpy.dw_hh_stack, axis=0))print("dw_hh_torch :\n",rnn_PyTorch.all_weights[0][1].grad.data.numpy())print("------------------------------------------------")# 打印NumPy和PyTorch的输入偏置梯度进行对比print("db_ih_numpy :\n",np.sum(rnn_numpy.db_ih_stack, axis=(0, 1)))print("db_ih_torch :\n",rnn_PyTorch.all_weights[0][2].grad.data.numpy())print("-----------------------------------------------")print("db_hh_numpy :\n",np.sum(rnn_numpy.db_hh_stack, axis=(0, 1)))print("db_hh_torch :\n",rnn_PyTorch.all_weights[0][3].grad.data.numpy())