流体力学或湍流理论中壁函数(wall function)
一、壁函数(wall function)概念
在流体力学或湍流理论中,壁函数是基于壁定律得到的无量纲速度 u + u^+ u+与无量纲壁距 y + y^+ y+之间的函数关系。
在对数层区域,速度剖面可以通过对数法则估计:
u + = 1 κ l n ( y + ) + B (1) u^+ = \frac{1}{\kappa} \, ln(y^+) + B \tag1 u+=κ1ln(y+)+B(1)
在靠近粘性子层壁,
u + = y + (2) u^+ = y^+ \tag2 u+=y+(2)
其中,
u + u^+ u+表示无量纲速度;
y + y^+ y+表示无量纲壁距离;
κ \kappa κ表示冯卡门常数;
B B B表示常数.
二、举例
假设光滑壁面的管道里的湍流中, κ ≈ 0.4 \kappa\approx 0.4 κ≈0.4和 B ≈ 5 B\approx 5 B≈5带入式(1)可绘制
u + = 2.5 l n ( y + ) + 5 (3) u^+ = 2.5 \, ln(y^+) + 5 \tag3 u+=2.5ln(y+)+5(3)
如图1所示。注意,不同的湍流边界层,其壁函数中的 κ \kappa κ和 B B B有所不同。
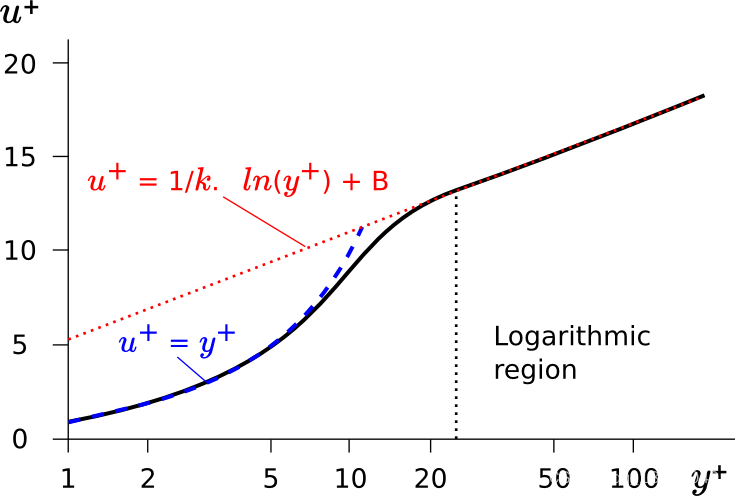 图1 光滑壁面的管道内壁函数关系
图1 光滑壁面的管道内壁函数关系
参考文献:
- Tennekes H., Lumley J. L. A First Course in Turbulence[M]. MIT press, 1972,152-165.