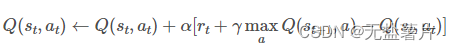免模型预测与控制
强化学习
- 免模型预测与控制
- 免模型预测
- 蒙特卡洛估计
- 时序差分估计
- 时序产分与蒙特卡洛的比较
- 免模型控制
- Q-learning
免模型预测
蒙特卡洛估计
蒙特卡洛估计方法在强化学习中是免模型预测价值函数的方式之一,本质是一种统计模拟方法,它的发展得益于电子计算机的发明。假设我们需要计算一个不规则图形的面积,这种情况下是很难通过规则或者积分的方式得到结果的。
而蒙特卡洛基于这样的想法:比如我们有一袋豆子,把豆子均匀地在一定范围内朝这个图形上撒,撒到足够多的数量时数一下这个图形中有多少颗豆子,这个豆子的数目就是图形的面积。当豆子越小撒的越多的时候,结果就越精确。此时我们借助计算机程序可以生成大量均匀分布坐标点,然后统计出图形内的点数,通过它们占总点数的比例和坐标点生成范围的面积就可以求出图形面积。
蒙特卡洛方法主要分成两种算法,一种是首次访问蒙特卡洛方法,另外一种是每次访问蒙特卡洛方法。首次访问蒙特卡洛方法主要包含两个步骤,首先是产生一个回合的完整轨迹,然后遍历轨迹计算每个状态的回报。注意,只在第一次遍历到某个状态时会记录并计算对应的回报。

时序差分估计
时序差分估计方法是一种基于经验的动态规划方法,它结合了蒙特卡洛和动态规划的思想。最简单的时序差分可以表示为式:
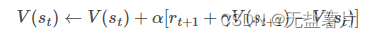
时序产分与蒙特卡洛的比较
- 时序差分方法可以在线学习每走一步就可以更新,效率高。蒙特卡洛方法必须等游戏结束时才可以学习。
- 时序差分方法可以从不完整序列上进行学习。蒙特卡洛方法只能从完整的序列上进行学习。
- 时序差分方法可以在连续的环境下(没有终止)进行学习。蒙特卡洛方法只能在有终止的情况下学习。
- 时序差分方法利用了马尔可夫性质,在马尔可夫环境下有更高的学习效率。蒙特卡洛方法没有假设环境具有马尔可夫性质,利用采样的价值来估计某个状态的价值,在不是马尔可夫的环境下更加有效。
免模型控制
Q-learning
为了解决控制问题,我们只需要直接预测动作价值函数,然后在决策时选择动作价值即 Q 值最大对应的动作即可。这样一来,策略和动作价值函数同时达到最优,相应的状态价值函数也是最优的。