《点云处理》提取点云内点和外点-编程知识

前言

关于内点（inliers）和外点（outliers）在点云处理方向上是个非常常见的名词。有时候，内点也会被称之为有效点，而外点会被称之为无效点。所谓有效和无效都是相对而言的，无效不一定是真的没有意义，并不等价于噪点，而有效也并不是绝对是想要的。有时候，可能既要内点，也要外点。之所以这么称呼，是想要从一整个大块的点云中将其分开来。通常，内点和外点具备不同的特征或者属性，根据这个属性，总能找到相应的算法将其分离。

举个例子，使用RANSAC进行平面拟合时，通常会设置一个距离阈值distance。RANSAC每次迭代都会从点云中任意取3个点，3个点在空间中确定了唯一的平面，可以得到平面方程。随即，遍历点云，计算每个点到该平面的欧氏距离，若距离大于设定的阈值distance，那么该点则是外点，这个点被认为是距离平面比较“远”的点，而点到平面的距离小于设定的阈值，则该点是内点，这个点被认为是距离平面比较“近”的点，或者干脆说在误差允许的范围内，该点在拟合的平面上。通常运行RANSAC算法后，会得到一个std::vector inliers动态数组，该数组中存放的一般就是内点的索引。

当然，除了拟合平面外，还有很多这样的例子，如欧式聚类。接下来就汇总一下，得到inliers之后，如何提取内点点云和外点点云。

方法一：

/// <summary>
/// 根据索引提取点云中的内点或者外点
/// </summary>
/// <param name="cloud">输入点云</param>
/// <param name="inliers">存放内点索引的数组</param>
/// <param name="cloud_out">输出点云</param>
/// <param name="is_true">输入true则提取内点点云，输入false则提取外点点云</param>
/// <returns>return true则表示提取成功，return false则表示提取失败</returns>
bool GetCloudByIndex(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud, const std::vector<int>& inliers, pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud_out, const bool& is_true)
{if (cloud == nullptr) return false;            // 判断输入点云是否为空if (cloud->points.size() < 10) return false;   // 判断输入点云的尺寸if (cloud_out == nullptr) cloud_out.reset(new pcl::PointCloud<pcl::PointXYZ>);  // 判断输出点云是否为空，如果为空则需要为其new出一个对象int PointSize = cloud->points.size();if (is_true){pcl::copyPointCloud(*cloud, inliers, *cloud_out);}else{std::vector<int> indices(PointSize);std::vector<int> outliers;std::iota(indices.begin(), indices.end(), 0);std::set_difference(indices.begin(), indices.end(), inliers.begin(), inliers.end(), std::back_inserter(outliers));pcl::copyPointCloud(*cloud, outliers, *cloud_out);}return true;
}

上述代码中，直接使用了pcl::copyPointCloud(*cloud, inliers, *cloud_out);提取点云，传入的第二个参数可以是inliers，也可以是outliers。输入点云cloud中所有点的索引或者说是下标肯定是0~n-1，0是第一个点的索引，n-1为最后一个点的索引，n是cloud包含的点数。

通常，想查看点云cloud中某个点的坐标，一般都会写成cloud->points[index]，这个index的范围就是0到n-1。std::iota(indices.begin(), indices.end(), 0);这句代码运行之后，就会得到一个cloud点云索引的容器，存放着0，1，2，3，4，5 … n-3，n-2，n-1。而inliers则是存放输内点索引的容器，std::set_difference(indices.begin(), indices.end(), inliers.begin(), inliers.end(), std::back_inserter(outliers));这句代码就是将点云cloud的全部索引indices与内点索引inliers进行比较，其中indices中有但是inliers中没有的索引值则存放进outliers。最后，用pcl::copyPointCloud(*cloud, outliers, *cloud_out);就提取到了外点点云。

运行时间对比如下图所示，可以发现内点运行时间还长一点，而外点提取时间还短一点。这个其实跟点的数量有关系，如果内点的数量多，当然就更耗时。但是总的来说，无论是提取内点还是外点，使用上述方法都是比较快的，而且很方便。
在这里插入图片描述

方法二：
除了上述方法之外，PCL库中特意集成有相应的方法提取点云的内点或者外点。
代码：

/// <summary>
/// 使用PCL库中pcl::ExtractIndices方法进行内点和外点的提取
/// </summary>
/// <param name="cloud">输入点云</param>
/// <param name="inliers">内点的索引数组</param>
/// <param name="cloudout">输出点云</param>
/// <param name="is_in">输入true则提取内点点云，输入false则提取外点点云</param>
/// <returns>return true则表示提取成功，return false则表示提取失败</returns>
bool ExtractCloudByIndices(const pcl::PointCloud<pcl::PointXYZ>::Ptr& cloud, const std::vector<int>& inliers, pcl::PointCloud<pcl::PointXYZ>::Ptr& cloudout, const bool& is_in)
{if (cloud == nullptr) return false;if (cloud->points.size() < 10) return false;if (cloudout == nullptr) cloudout.reset(new pcl::PointCloud<pcl::PointXYZ>);pcl::PointIndices::Ptr pinliers(new pcl::PointIndices());pinliers->indices.assign(inliers.begin(), inliers.end());pcl::ExtractIndices<pcl::PointXYZ> extractor;extractor.setInputCloud(cloud);extractor.setIndices(pinliers);extractor.setNegative(!is_in); //如果设为true,可以提取指定index之外的点云extractor.filter(*cloudout);return true;
}

上述代码中extractor.setNegative(!is_in);就是设置提取内点还是外点的成员函数。如果extractor.setNegative(true);即输入的是true，则提取除了inliers以外的，也就是外点的点云，而extractor.setNegative(false);才是提取inliers索引的点云，与方法一中的习惯相反，为了调整成一致，所以传入的是!is_in，而不是is_in。这个时候就与方法一保持一样的习惯了。

此外，还有一点不同的是pcl::ExtractIndices所需要的传入的索引不是std::vector 而必须是pcl::PointIndices::Ptr。其实这两种数据结构是可以互相转化的，所以用 pinliers->indices.assign(inliers.begin(), inliers.end());这句代码进行了一次转化。当然，在使用PCL库中算法时，有时候得到的不一定是std::vector，而是pcl::PointIndices::Ptr。这个就看每个人的习惯和喜好去封装函数了，也可以封装成一个传参为pcl::PointIndices::Ptr数据的函数。

运行结果如下：
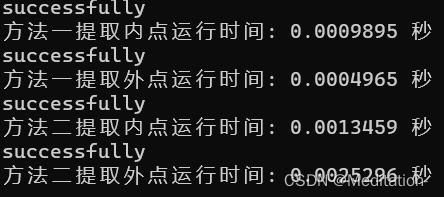
在这里插入图片描述
可以从结果看出，方法二的耗时要比方法一长“很多”。具体使用哪种方法进行点云内点或者外点的提取则是要看个人习惯了。