直接选择排序:
这里我用两个变量同时找出最小值和最大值。
注意:若begin为最大值,maxi即为最大值的下标,若将最小值与其交换,最大值的下标此时就不再是maxi,而变为mini了,故此时要调整maxi的位置
直接选择排序的时间复杂度 O(N^2)
void PrintArray(int* a, int n)
{int i;for (i = 0; i < n; i++){printf("%d ", *(a + i));}
}
void Swap(int* a, int* b)
{int tem = *a;*a = *b;*b = tem;
}
//直接选择排序
void SelectedSort(int* a, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin, maxi = end;for (int i = begin; i <= end; i++){if (a[i] < a[mini])mini = i;if (a[i] > a[maxi])maxi = i;}Swap(&a[begin], &a[mini]);//如果begin与maxi重叠,需要修正maxi此时max被换到了mini的位置上if (begin == maxi)maxi = mini;Swap(&a[maxi], &a[end]);begin++;end--;}
}
void TestSelectedSort()
{int a[] = { 3,5,2,7,8,6,1,9,4,0 };SelectedSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}堆排序:
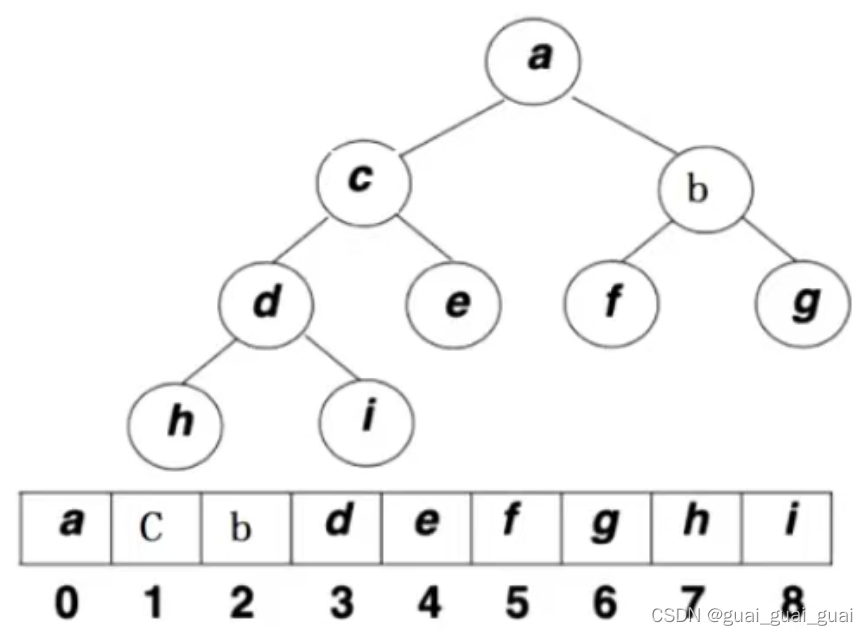
- 堆的逻辑结构是一颗完全二叉树
- 堆的物理结构是一个数组
数组下标的父子节点关系
leftchild=parent*2+1
rightchild=parent*2+2
parent=(child-1)/2
堆的两个特性:
- 结构性:用数组表示的完全二叉树
- 有序性:任一节点的节点的关键字是其子树所有结点的最大值或最小值
- “最大堆(MaxHeap)”,也称“大顶堆”:最大值
- “最小堆(MinHeap)”,也称“小顶堆”:最小值
- 大堆要求:树中所有的父亲都大于等于孩子,堆顶的数据是最大的
- 小堆要求:树中所有的父亲都小于等于孩子,堆顶的数据是最小的
建小堆
向下调整算法
前提:左右子树都是小堆
从根节点开始选出左右孩子中小的那一个,跟父亲比较,如果比父亲小就交换,然后再继续往下调
建堆的时间复杂度为O(N)。
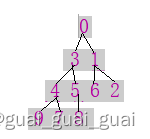
如果左右子树不是小堆,该怎么建小堆呢?
我们可以倒着从最后一棵子树开始调,倒着走,从倒数第一个非叶子的子树开始调,即为从8开始,那如何找到8呢,只需找出最后一个数据的下标利用父子节点的关系求出即可,即(n-1)-1/2.

若是升序,应该建大堆还是小堆呢?我第一次认为是小堆,实则不然,若是小堆,小堆会把最小的数放在第一位,选择排序是通过堆来选树,最小数此时在堆顶已被选出,此时就要在剩下的树里选树,但此时新树的结构就已经乱了,之前所建的小堆已经不复存在,需要再建小堆才能选出下一个树,建堆的时间复杂度为O(N),这样建堆所带来的效率优势就没了。故升序不能建小堆

正确的应该是建大堆,将第一个数和最后一个数交换,此时最后一个数为最大的数,不把它看成是堆里面的数,前n-1个数向下调整,选出次大的数,再跟倒数第二个位置交换,以此类推,此时中间堆的结构未改变。

堆排序的时间的复杂度为O(N*logN)
堆排序代码如下:
//堆排序
//建大堆
void Swap(int*a, int*b)
{int tem = *a;*a = *b;*b = tem;
}
//向下调整算法
void AdjustDown(int* a, int n, int root)
{int parent = root;int child = parent * 2 + 1;//默认是左孩子while (child<n){//1.选出左右孩子中最大的一个if (child+1<n&&a[child + 1] > a[child])//防止数组越界,所以要加child+1<n{child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}//若孩子本来就比父亲小,因为大堆的每棵树都是大堆,说明此时堆已经建好,break即可elsebreak;}
}
void HeapSort(int* a, int n)
{//把数组建成堆 倒着走for (int i = (n - 1 - 1) / 2; i >= 0; i--)//n-1为最后一个元素的下标,(n-1-1)/2即为parent{AdjustDown(a, n, i);}//排升序,建大堆int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
void PrintArray(int* a, int n)
{int i;for (i = 0; i < n; i++){printf("%d ", *(a + i));}
}
void TestHeapSort()
{int a[] = { 3,5,2,7,8,6,1,9,4,0 };HeapSort(a, sizeof(a) / sizeof(int));PrintArray(a, sizeof(a) / sizeof(int));
}int main()
{TestHeapSort();return 0;
}