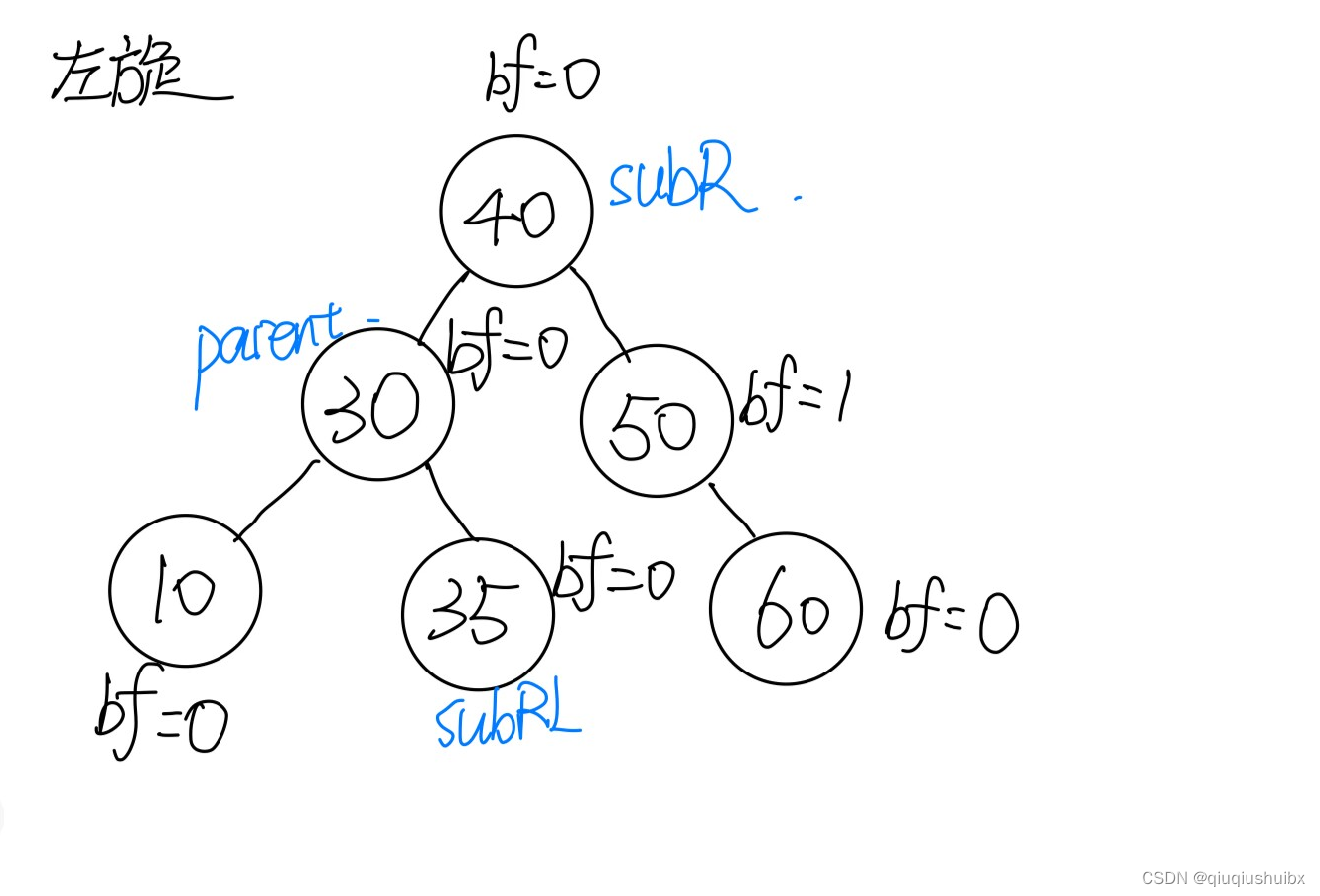数据结构 AVL树概念以及实现插入的功能(含Java代码实现)-编程知识

为啥要有avl树

avl树是在二叉搜索树下的一种进阶形式,是为了防止二叉搜索树在极端情况下产生的链表化的场景,从而在二叉搜索树的基础上,加上了某些条件来阻止这种极端情况的产生,但不是保证完全平衡,而是放开了一定的条件,使得这种情况不那么难以满足.(条件:左右子树的高度差的绝对值不大于1) ,我们在发现大于1的时候可以使用左右旋转的方式来调整数的形态,从而保证了查找的时候有近似于O(logN)的性能.

缺点:

当然,有得必有失,这样也带来了一定的损耗:浪费了空间来保存新的变量,每次插入都判断是否满足条件,这样导致了插入的效率变低,这也使得这种二叉树不适合连续多次的插入和修改数据.

如果我们需要持续多次的插入数据,那么也有更进一步的数据结构 --- 红黑树

AVL树的定义

平衡因子

定义为每个节点的左子树和右子树的高度差(左减去右,右减去左都可以表示)

本文使用右减左表示高度差的定义

例如空树的高度差就是0,这就代表着平衡,

当高度差达到-1,就表示左子树高了,但是还在允许的范围之间,无需调整

当高度差达到1,就代表右子树高了,也在允许的范围之内

当左右子树的高度差超过这个范围(绝对值大于2的时候),那么我们就得需要实现左右旋转来满足这种结构的查找效率.

节点代码结构
static class TreeNode{public int val;public int bf;//balance factor 平衡因子public TreeNode left;//左孩子public TreeNode right;//右孩子public TreeNode parent;//父节点public TreeNode(int val) {this.val = val;}}

实现插入功能

总体思路:

1.按照平衡二叉树的比较方式去寻找到应该插入在的节点

2.插入完了修改一下bf(平衡因子)的值

3.判断是否平衡

3.1 bf = 0直接跳出循环即可

3.2 bf = 1 或 bf = -1就继续向上寻找

3.3 bf = 2考虑左旋右旋修改avl树的结构

以下会包含四种失衡以及解决方案

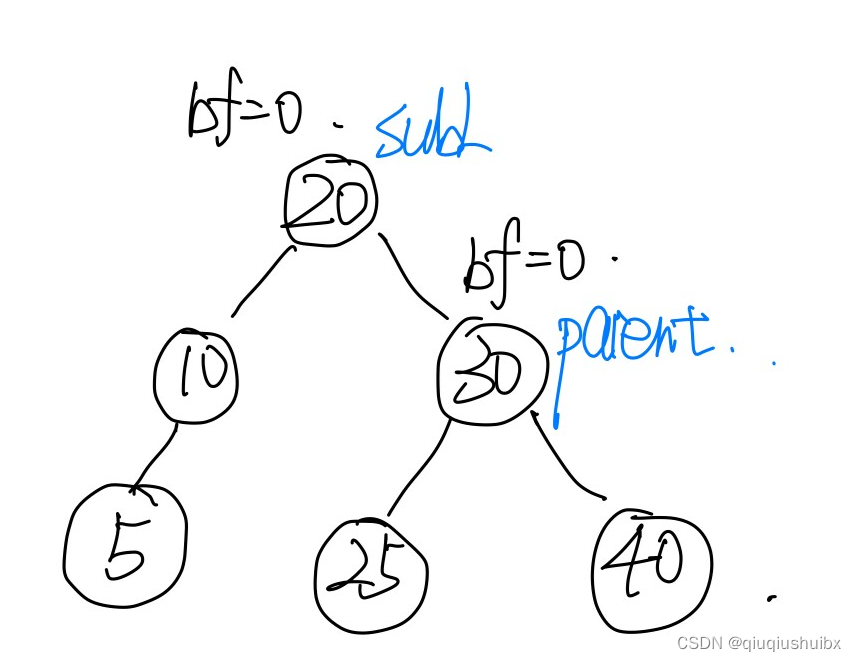
1.LL类型

我们能很容易发现这种不平衡式因为左子树太深而导致的,此时我们要使用右旋来保证结构的正确.

具体步骤就是

1.将subL作为根节点

2.subLR作为parent的左孩子

3.parent作为subL的右孩子

此时我们发现subL和parent的平衡因子都会变成0

2.RR类型

此时我们明显发现右子树的深度要高于左子树两个节点

此时我们就需要进行左旋来调整整体结构的状态

整体步骤与之前类似

1.将subR提出来当根节点

2.subRL作为parent的右子树

3.parent作为subR的左子树

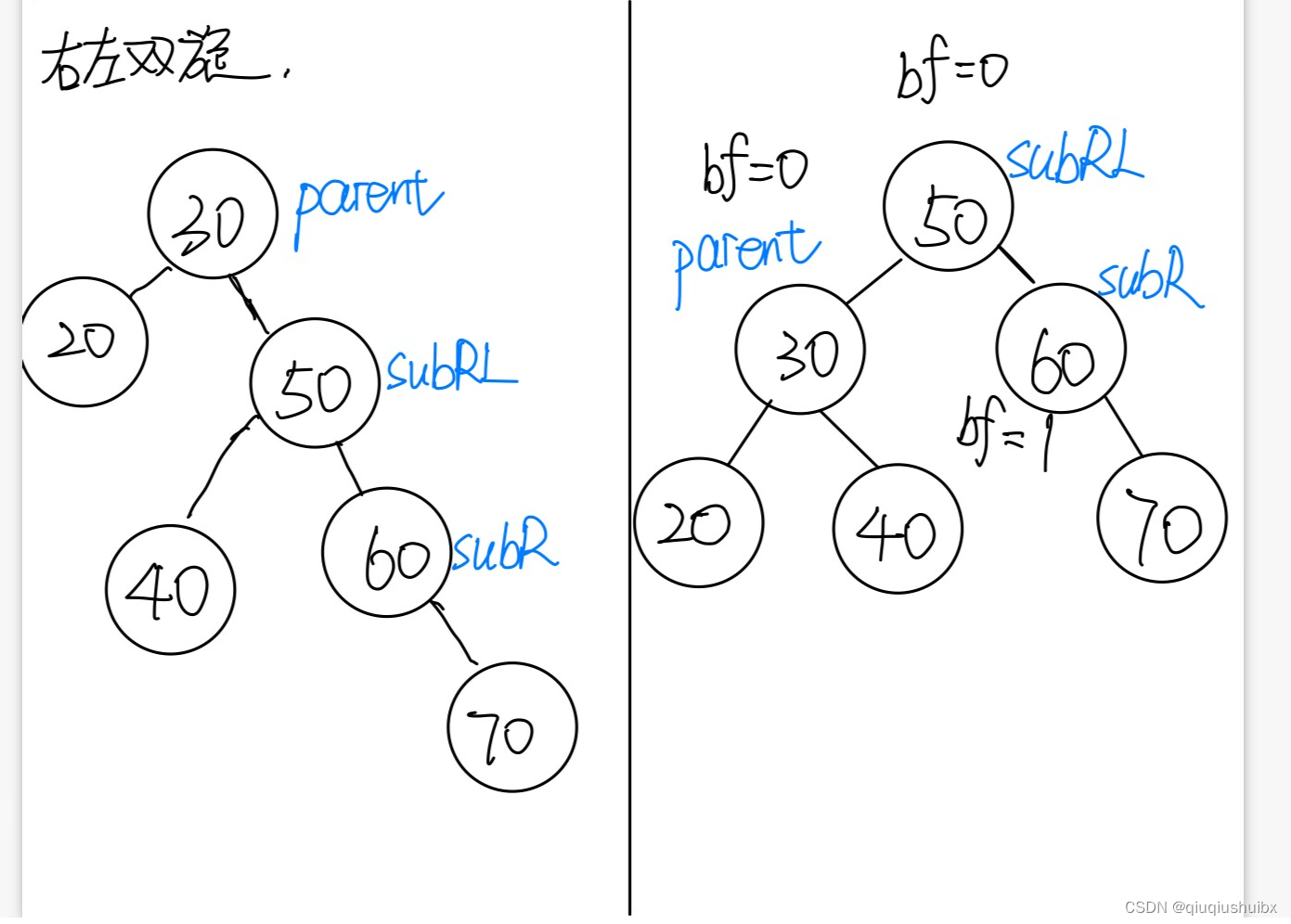
3.RL类型

这个你可以理解是在右子树深的情况下子树是左子树比较深,而前面的方式是左右子树的子树也是呈现同一趋势的.

执行方式

1.先对右子树进行一次右旋,这时候我们发现总体又一次呈现了RR型状态

左旋即可达成平衡的目标

这里如果我们插入的是节点值是55又会有不一样的平衡值

4.LR类型

执行方式也是一样的,我们对左子树进行左旋,再对整体进行右旋即可

这里我直接给出操作形式,其实这里插入的是25也会有另一种结果,在代码中有所体现,读者可自行画图推导

完整avl树插入代码

public class AVLTree {static class TreeNode{public int val;public int bf;//balance factor 平衡因子public TreeNode left;//左孩子public TreeNode right;//右孩子public TreeNode parent;//父节点public TreeNode(int val) {this.val = val;}}public TreeNode root;//根节点public boolean insert(int val){TreeNode node = new TreeNode(val);if(root == null) {root = node;return true;}TreeNode cur = root;TreeNode parent = null;while(cur != null){if(val < cur.val){parent = cur;cur = cur.left;}else if(val == cur.val){return false;}else{parent = cur;cur = cur.right;}}if(parent.val>val){parent.left = node;}else{parent.right = node;}node.parent = parent;//调节负载因子cur = node;//负载因子的修改while(parent != null){//先看cur是parent的左还是右//平衡因子为右 - 左if(cur == parent.right){//右树高,因子++parent.bf++;}else{//左树高parent.bf--;}//检查平衡因子变化完了是多少if(parent.bf == 0){break;}else if(parent.bf == 1 || parent.bf == -1){//继续向上判断修改平衡因子//因为等于1和-1只代表当前子树平衡cur = parent;parent = parent.parent;}else{//2或者-2的情况,考虑左旋右旋if(parent.bf == 2){if(cur.bf == 1){rotateLeft(parent);}else{//-1的情况rotateRL(parent);}}else{//-2的情况if(cur.bf == 1){rotateLR(parent);}else{//-1的情况rotateRight(parent);}}break;}}return true;}//左单旋private void rotateLeft(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if(subRL != null){subRL.parent = parent;}TreeNode pParent = parent.parent;parent.parent = subR;if(root == parent){root = subR;root.parent = null;}else{if(pParent.left == parent){pParent.left = subR;}else{pParent.right = subR;}subR.parent = pParent;}subR.bf = parent.bf = 0;}//右单旋private void rotateRight(TreeNode parent){//画图便于理解TreeNode subL = parent.left;TreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if(subLR != null){subLR.parent = parent;}//必须先记录TreeNode pParent = parent.parent;parent.parent = subL;//检查当前是否为根节点if(parent == root){root = subL;root.parent = null;}else{//此刻的parent也不一定是根节点,还是有左右树的if(pParent.left == parent){pParent.left = subL;}else{pParent.right = subL;}subL.parent = pParent;}subL.bf = 0;parent.bf = 0;}//左右双旋private void rotateLR(TreeNode parent){TreeNode subL = parent.left;TreeNode subLR = subL.right;int bf = subLR.bf;rotateLeft(parent.left);rotateRight(parent);if(bf == -1){subL.bf = 0;subLR.bf = 0;parent.bf = 1;}else if(bf == 1){subL.bf = -1;subLR.bf = 0;parent.bf = 0;}}//右左双旋private void rotateRL(TreeNode parent) {TreeNode subR = parent.right;TreeNode subRL = subR.left;int bf = subRL.bf;rotateRight(parent.right);rotateLeft(parent);if(bf == 1){parent.bf = -1;subR.bf = 0;subRL.bf = 0;}else if(bf == -1){parent.bf = 0;subR.bf = 0;subRL.bf = 1;}}//验证当前树public void inorder(TreeNode root){if(root == null){return;}inorder(root.left);System.out.println(root.val+" ");inorder(root.right);}private int height(TreeNode root){if(root == null){return 0;}int left = height(root.left);int right = height(root.right);return Math.max(left+1,right+1);}public boolean isBalanced(TreeNode root){if(root == null){return true;}int left = height(root.left);int right = height(root.right);//判断平衡因子是否有问题if (right-left != root.bf){System.out.println("这个节点" + root.val +"平衡因子异常");return false;}return Math.abs(left-right)<=1&&isBalanced(root.left) && isBalanced(root.right);}public static void main(String[] args) {int[] arr= new int[]{4, 2, 6, 1, 3, 5, 15, 7, 16,14};AVLTree avl = new AVLTree();for (int i = 0; i < arr.length; i++) {avl.insert(arr[i]);}System.out.println(avl.isBalanced(avl.root));}
}