前言
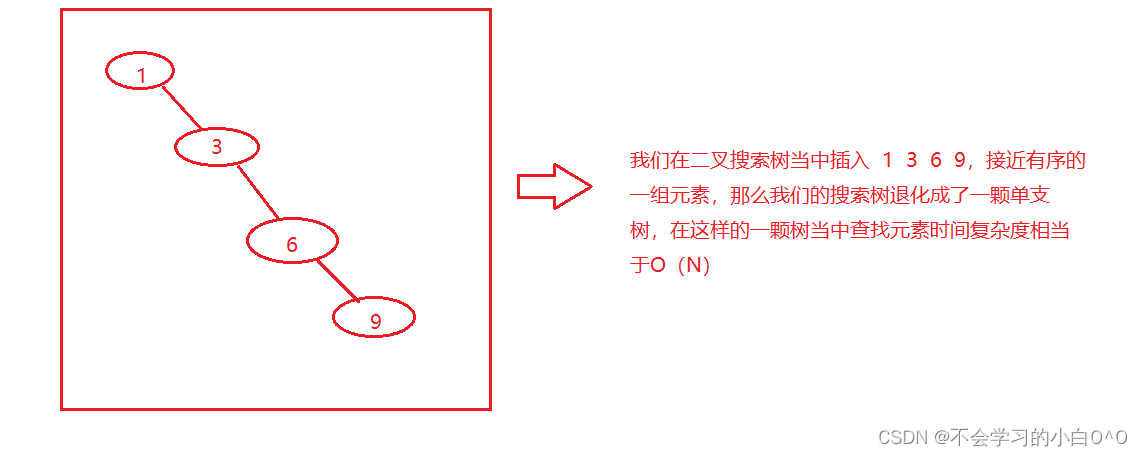
二叉树搜索树是存在一定的缺陷问题的,当我们要插入的数据是有序,或者说接近于有序,,二叉搜索树及有可能退化为单支树,查找元素相当于在顺序表当中搜索元素,效率低下
---------------------------------------------------------------------------------------------------------------------------------
AVL树的概念
解决上述问题的方法是两位俄罗斯科学家发明的: 当向二叉搜索树当中插入新节点后,如果能保证每个节点的左右子树高度差的绝对值不超过1(超过对树当中的节点做调整),降低树的高度,从而减少平均搜索长度
一颗AVL树或者是空树,或者是具有以下性质的二叉搜索树:
1.它是左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过(-1 / 0 /1) 平衡因子:右子树的高度-左子树的高度

如果一颗二叉搜索树是高度平衡的,它就是AVL树,如果它有n个节点,其高度可保持在log_2(N),那么搜索的时间复杂度以2为底N的对数!!!
log以2为底n的对数是查找效率非常高的了,假设将我们全中国人口14亿人的数据保存在这样的一颗树当中,那么只需要查找31次,最多31次,高度次,是非常恐怖的!!!
-----------------------------------------------------------------------------------------------------------------------
实现AVL树
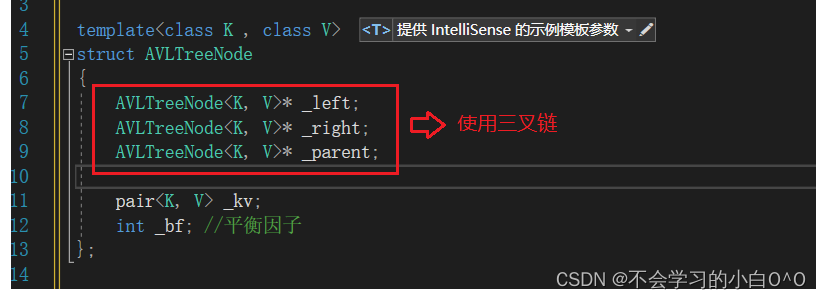
为何我们在这里使用三叉链呢??
当我插入一个新节点之后,这棵树还是不是平衡树,我们就看高度差,不过呢平衡因子就是高度差的一个结果,在插入新节点之后我们得想办法更新平衡因子,更新的是祖先的平衡因子

----------------------------------------------------------------------------------------------------------------------
insert插入的实现
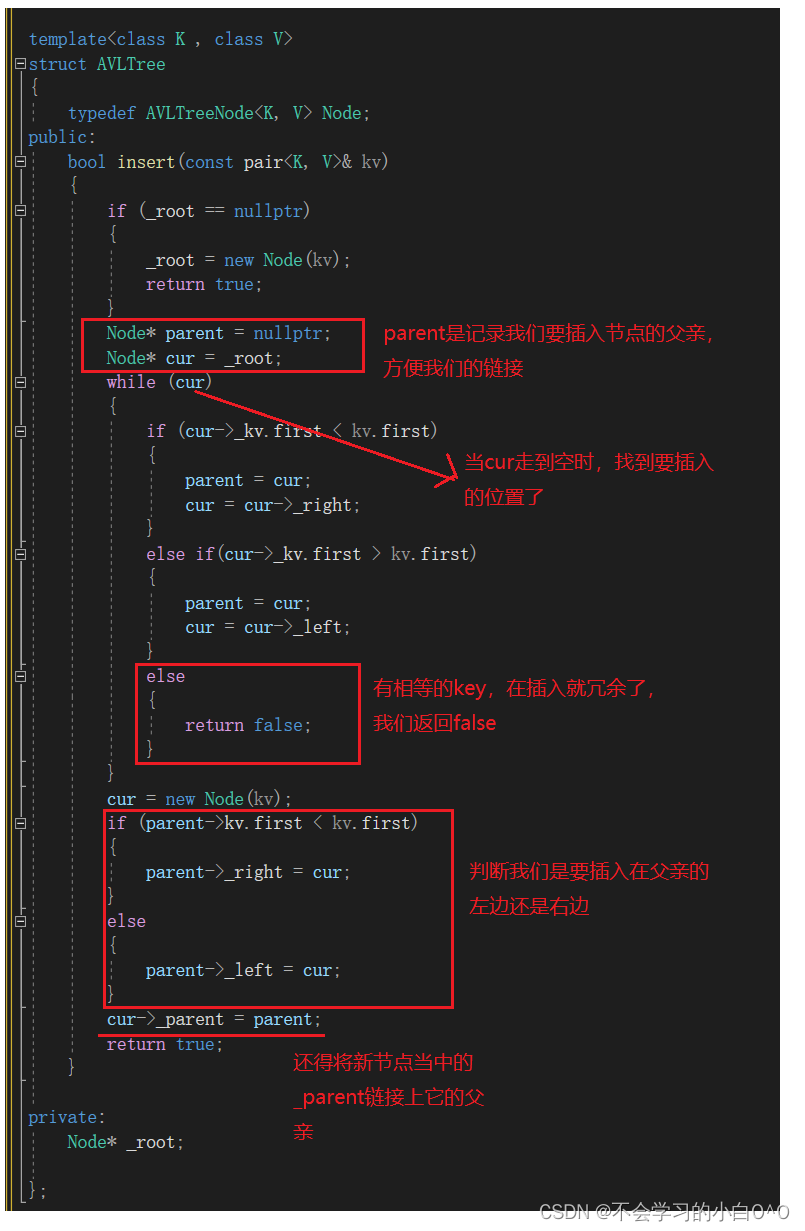
按照我们以前的搜索树的insert,到这一步也就结束了,但是我们这里插入之后,我们得控制平衡
有可能插入之后还是平衡的,也可能插入之后,不平衡了
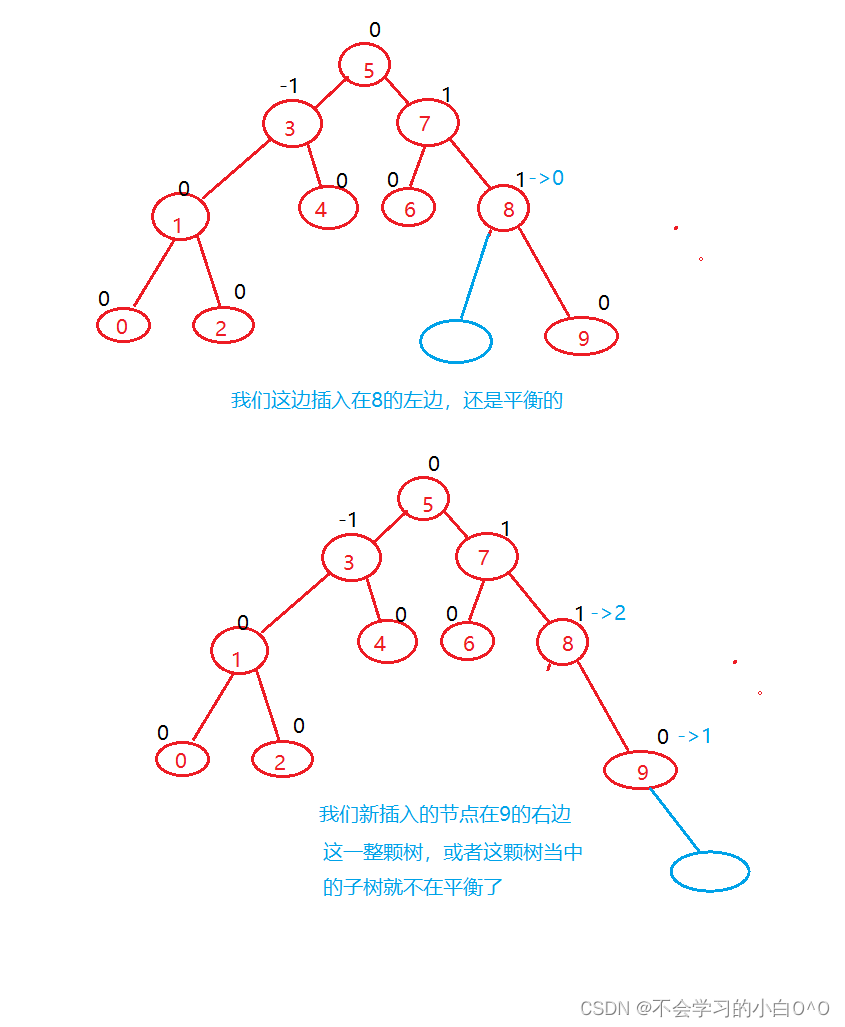
我们在判断这颗树,或者子树是否平衡时,是通过平衡因子判断的,所以在判断是否平衡之前,得先更新平衡因子
更新平衡因子的规则:
1.新增在右,parent->_bf++ ,新增在左,parent->_bf--;
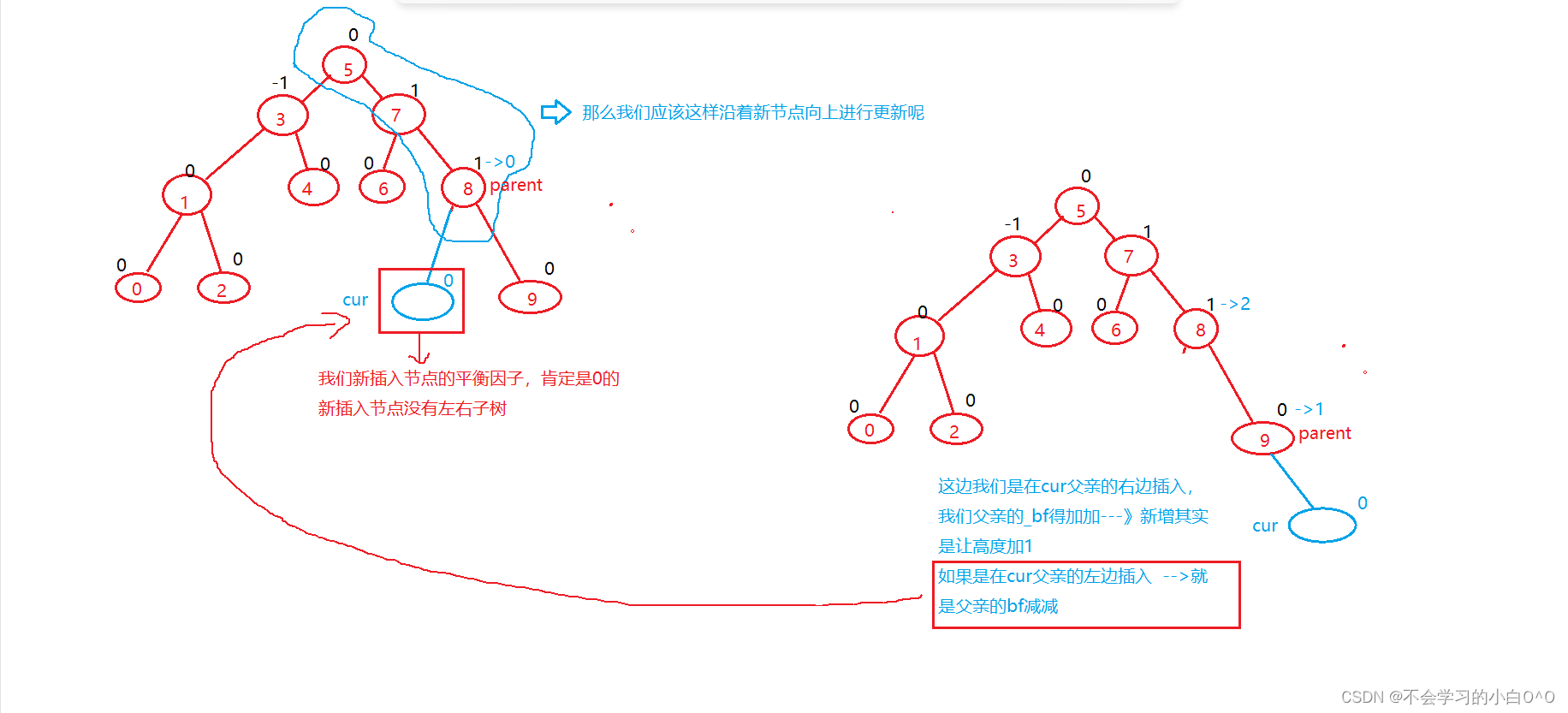
2.更新后,parent->_bf == 1或者-1 ,说明parent插入之前的平衡因子是0,说明左右子树高度相等,插入有一边高,parent的高度变了,继续往上更新
更新后,parent->_bf == 1 or -1 , 1代表右边高, -1代表左边高 ,这里要不要继续往上更新平衡因子的因素取决于,parent子树的高度是否变化,parent的平衡因子变为-1或者1,高度肯定的变了,为什么呢? 因为++ 或者 -- 之后变为 -1 或者1 说明在不插入新节点之前是左右子树高度是一样的
我们在这里有没有可能parent的平衡因子是 2或者 -2 ,加加 减减之后变为 1或者-1 呢??肯定是不可能的,如果之前是2或者-2的画早就不平衡了,之前就应该做调整
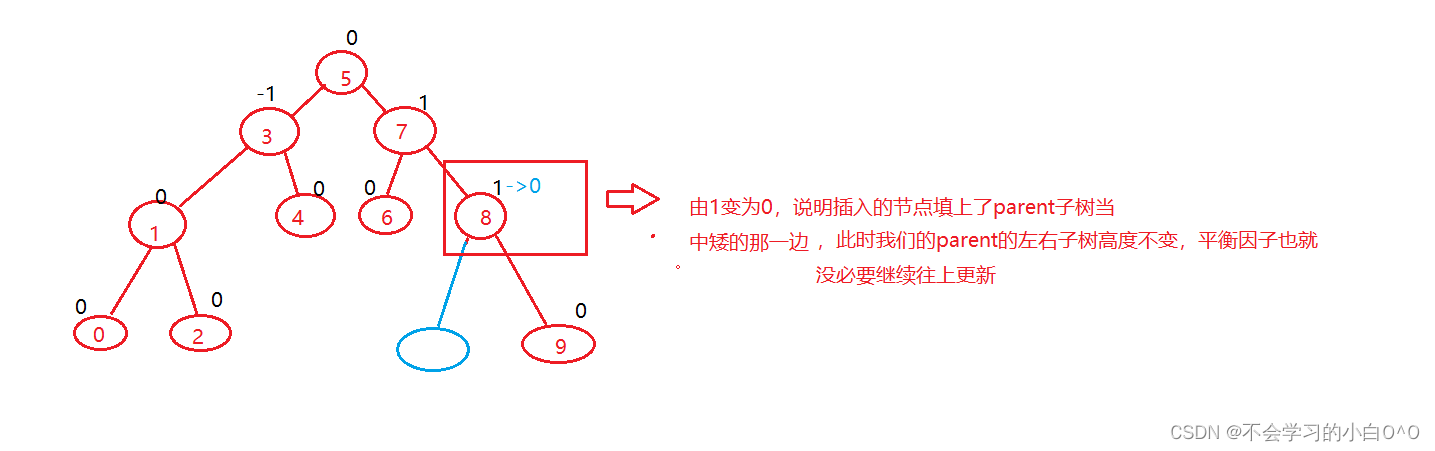
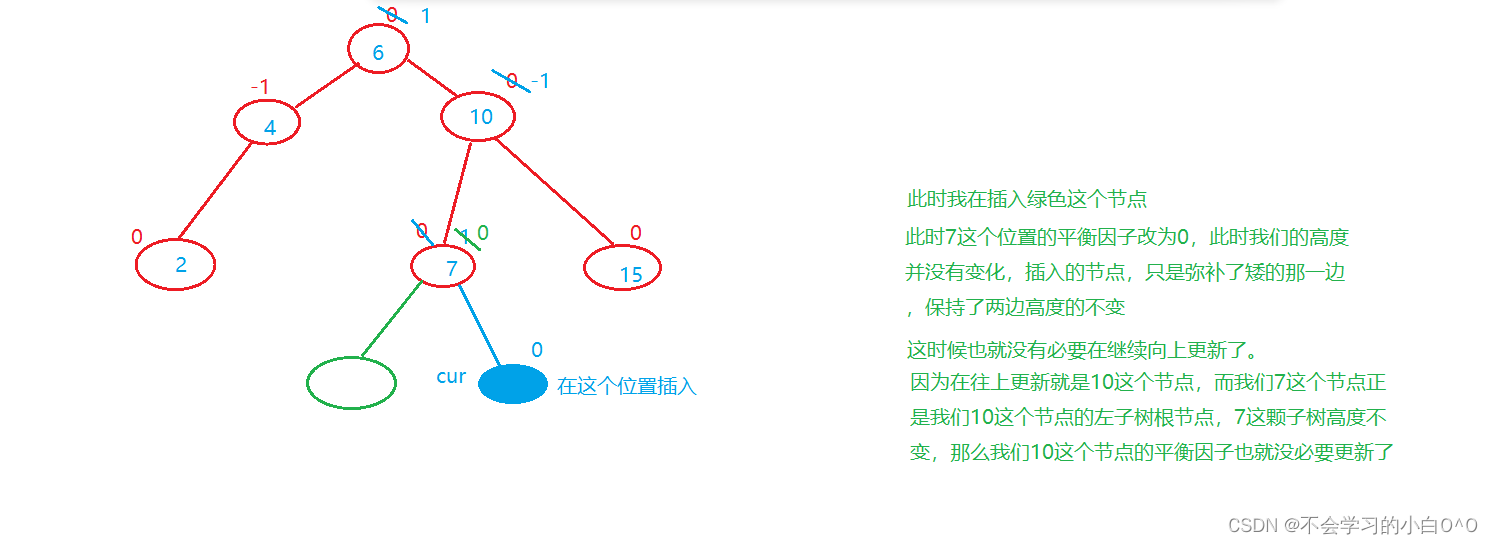
3.更新后,parent->_bf ==0 ,说明parent插入之前的平衡因子 -1 或者 1 加加或者减减一下,说明左右子树一边高一边低,插入之后,两边一样高,说明插入填上了矮的那一边,parent所在的子树高度不变,不需要继续向上更新
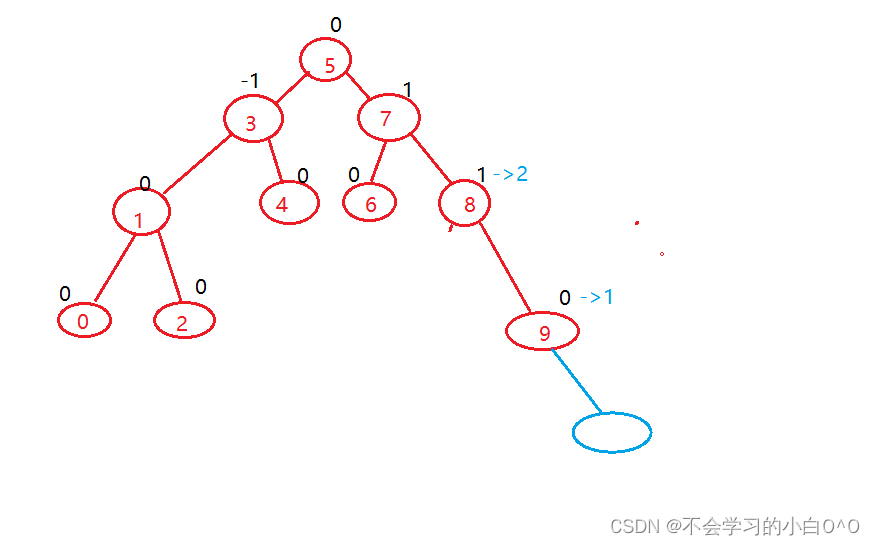
4.更新后,parent->_bf == 2或者-2 ,说明parent插入前的平衡因子是 1or -1 ,说明在插入之前已经是平衡的临界值了,现在插入变成2或者-2 ,说明打破平衡,parent所在的子树,需要进行旋转处理
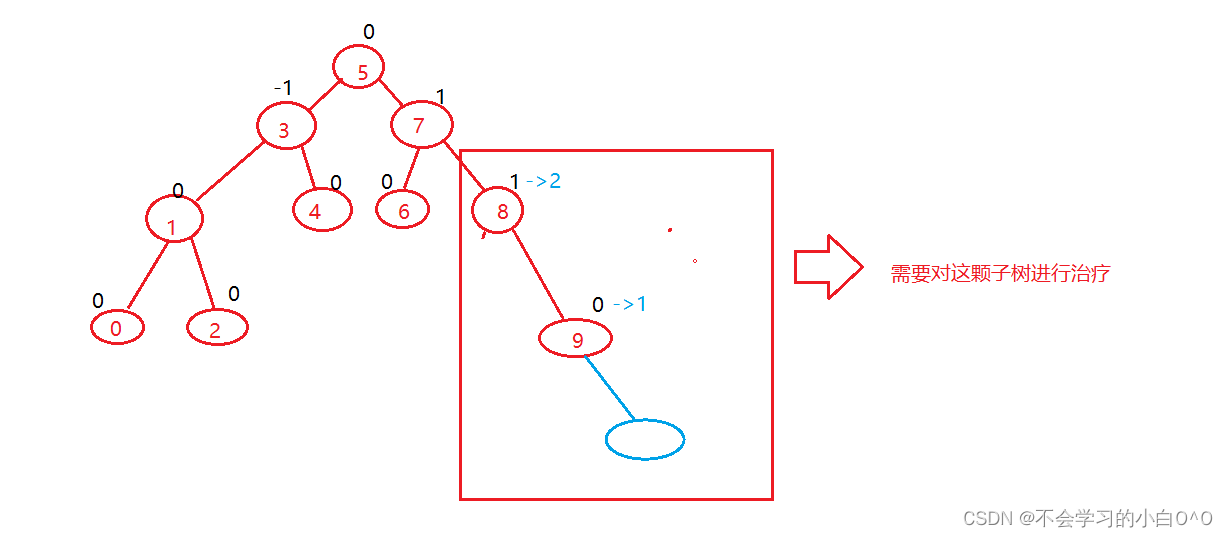
5.更新后,parent->_bf >2 or parent->_bf < -2 ,不可能,如果存在则说明插入之前就不是AVL树,那需要去检查之前的操作问题

此时这颗树,并没有发生旋转,但是快要发生旋转了,倾向于旋转了,好几个节点的平衡值都在临界值。
-------------------------------------------------------------------------------------------------------------
我们现在写更新平衡因子的代码 --> 最坏的情况就是不断更新,更新到根节点,也可能中间就停止了
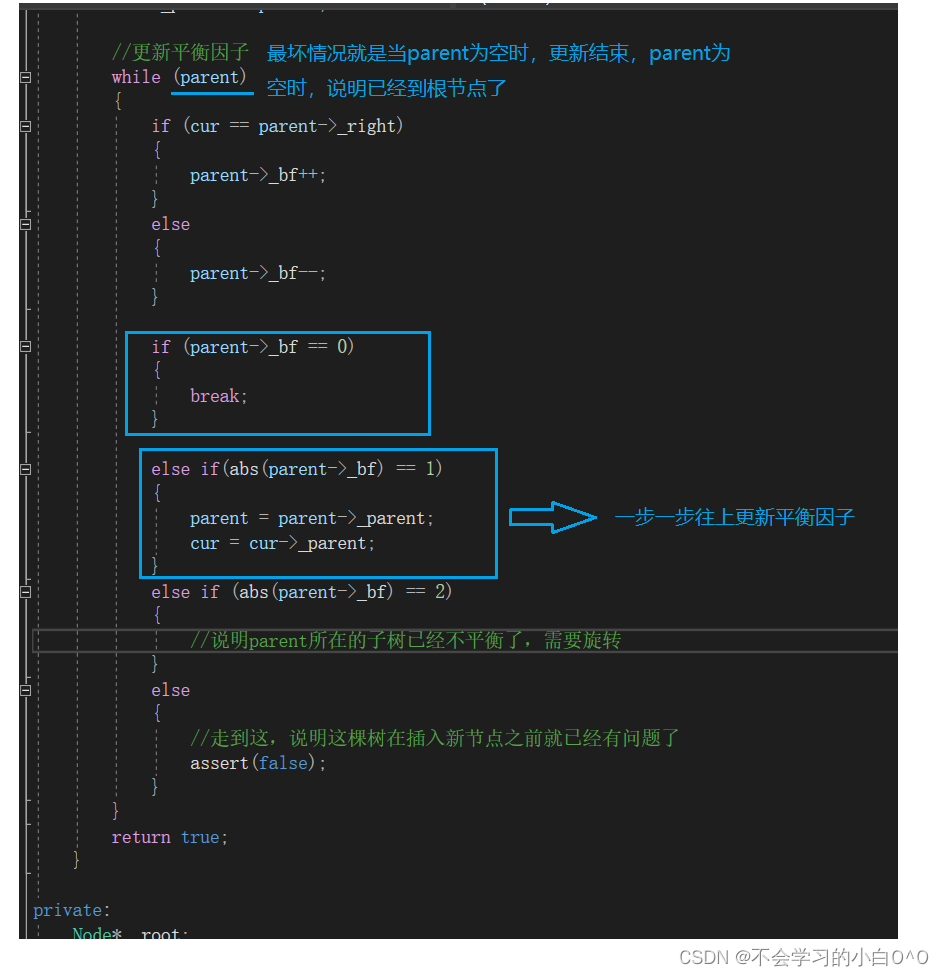
接下来就是要处理我们的旋转问题了
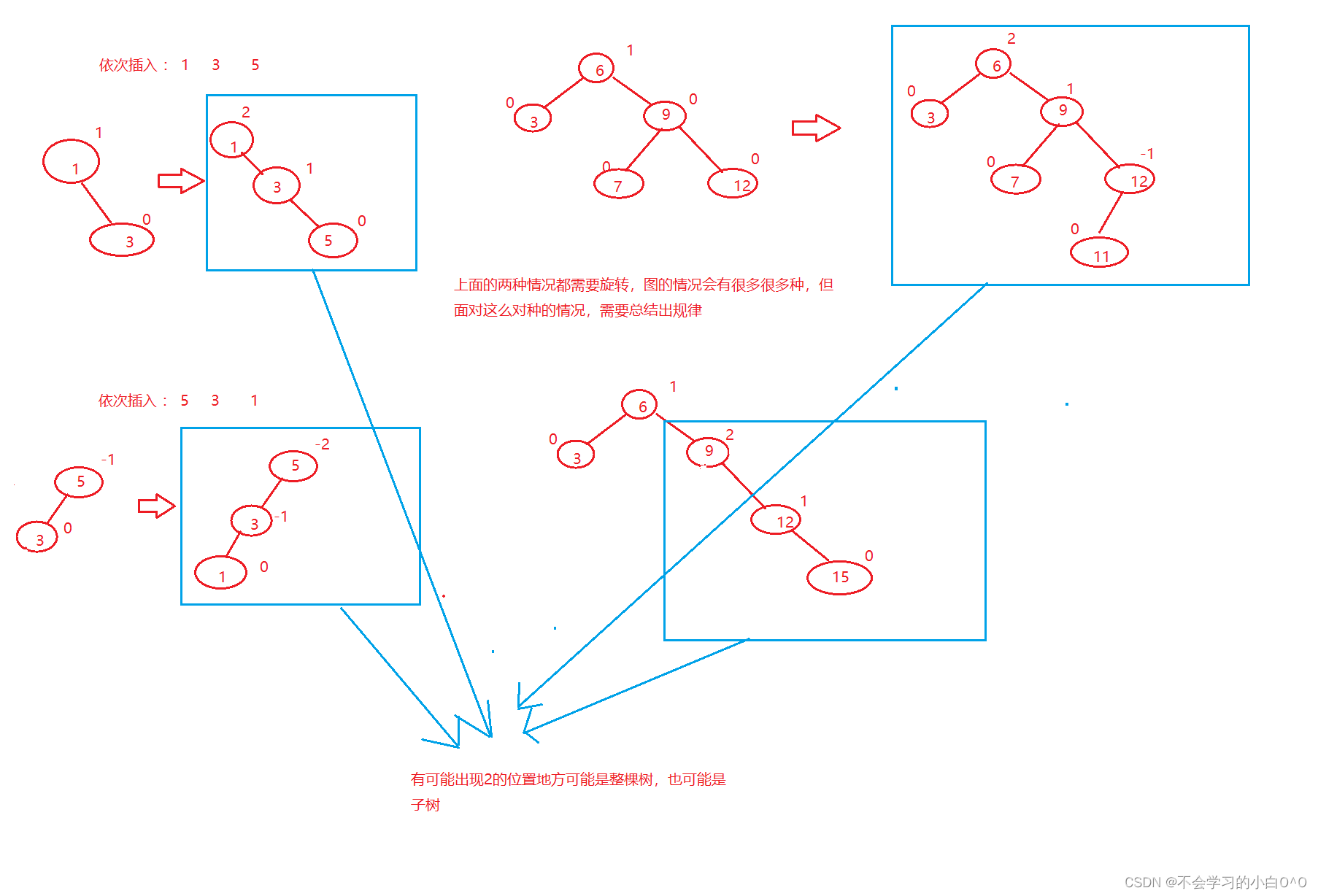
在这里我们需要想办法去处理,无论是整颗树,还是子树
我们在这里处理的原则 :
1.旋转成平衡树
2.保持搜索树的规则
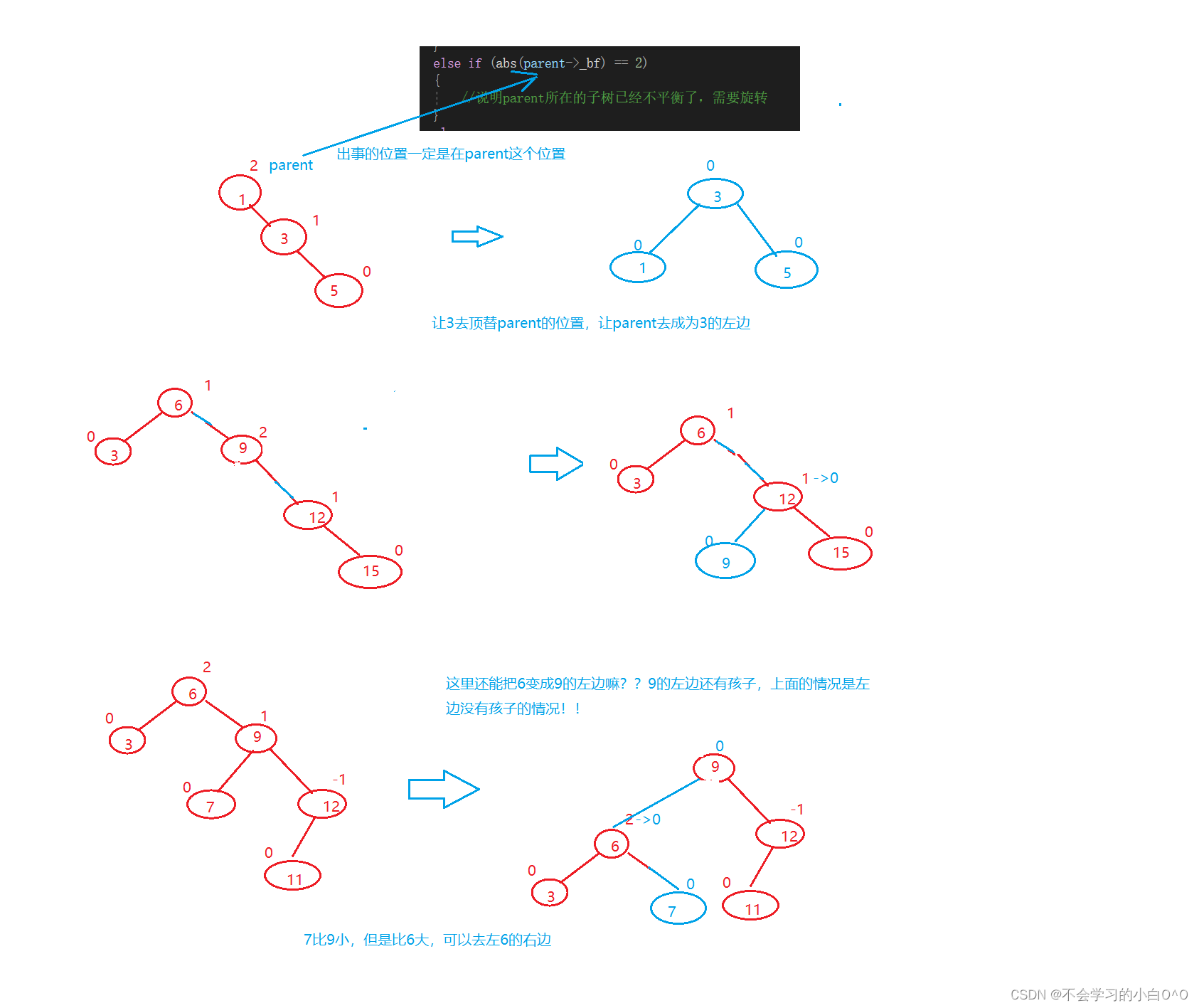
对上面的情况网上有人做了归类
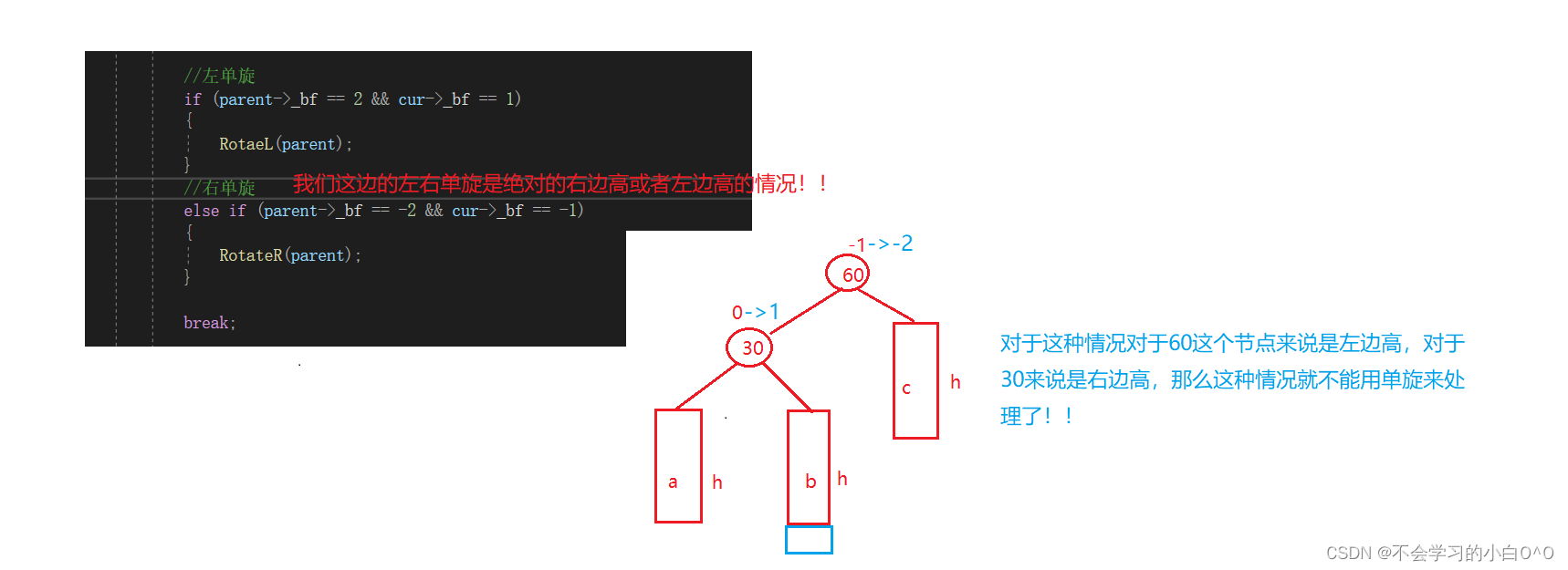
左单旋
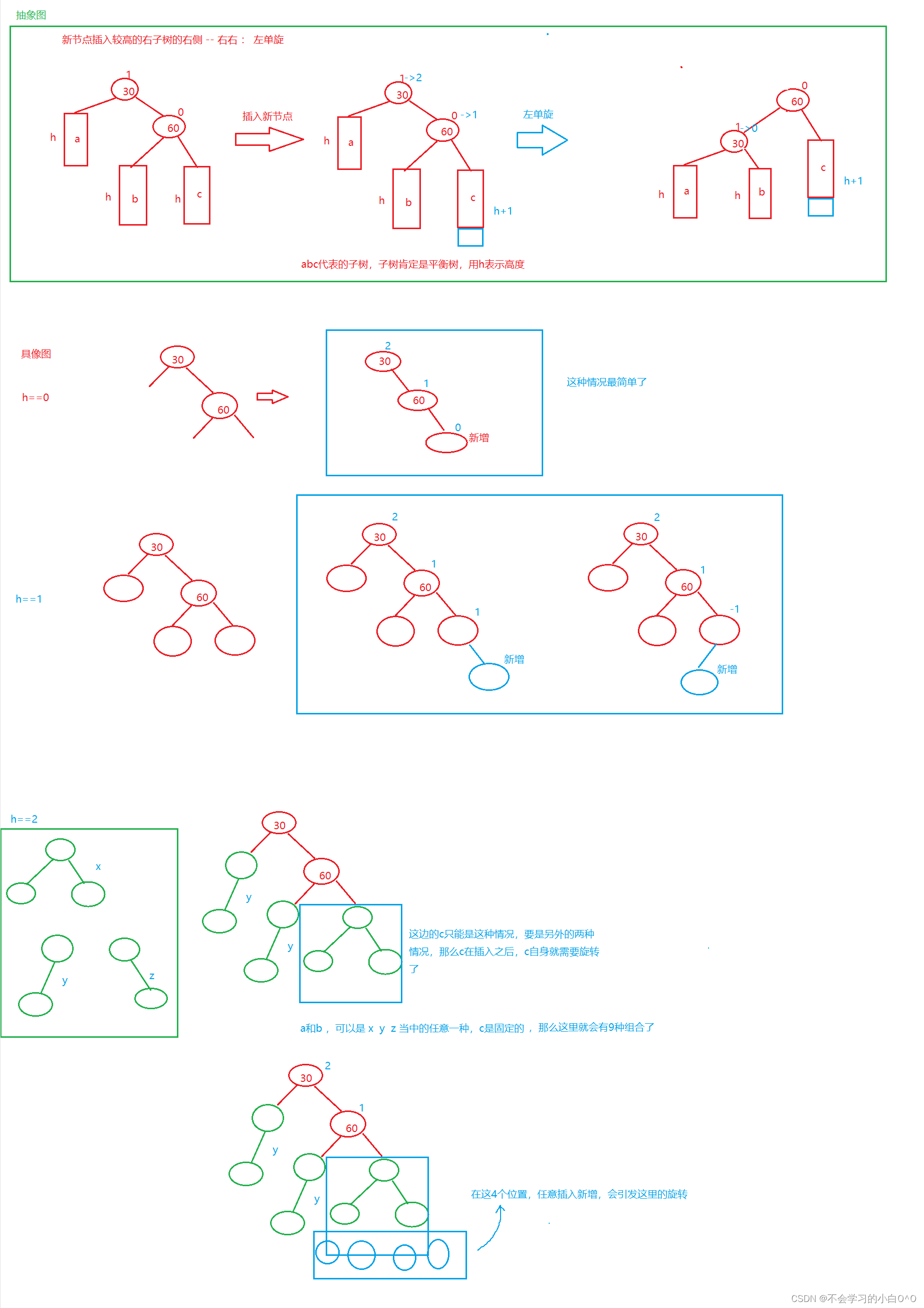
当h==2的时候,就已经有36种情况了
当h==3时,情况就更多了
如果我们要列举这里的情况,是无穷无尽的,但是对于上面情况当中的哪一种,我们的处理动作都是一样的

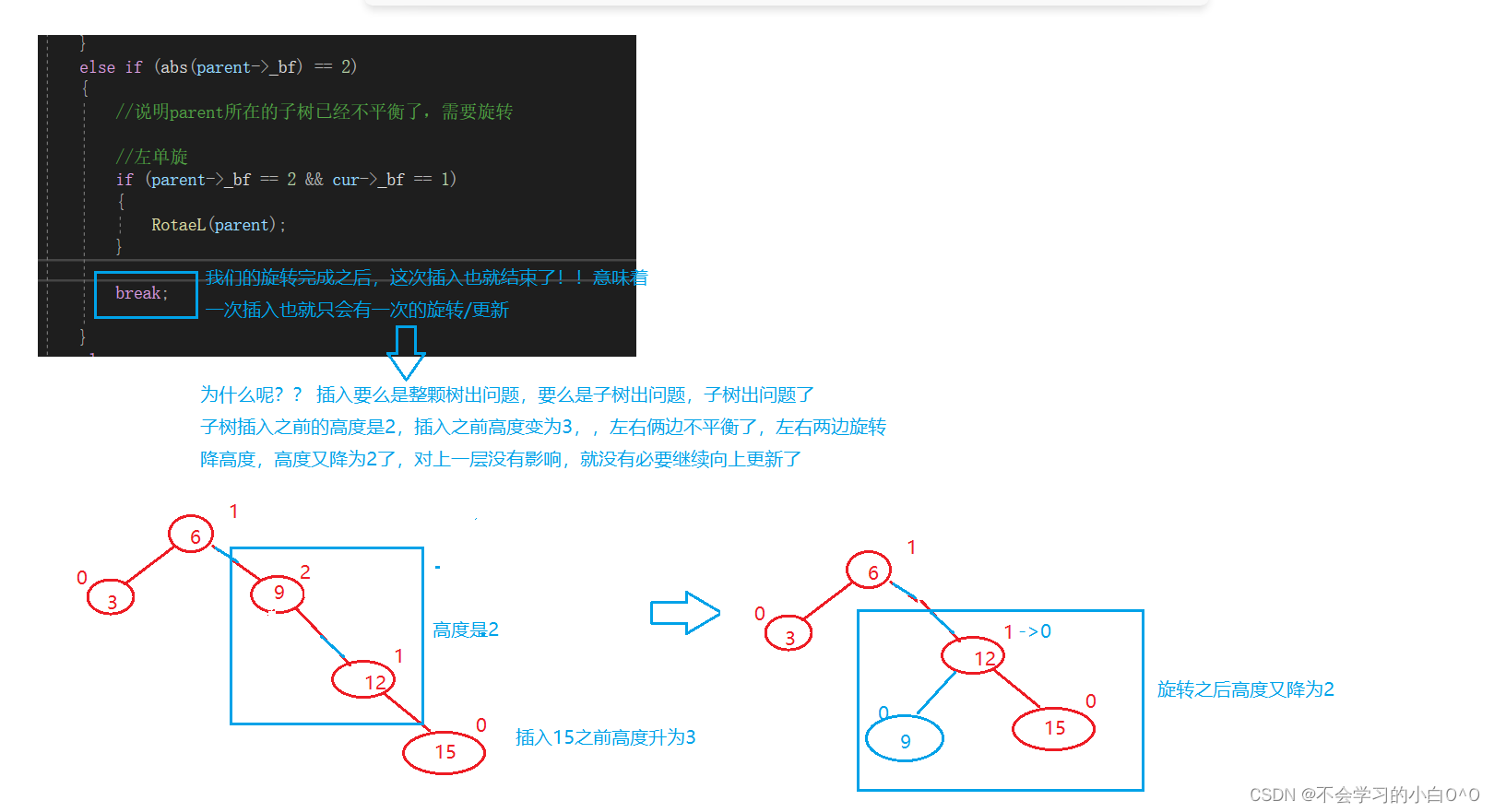
所以插入的时间复杂度是 高度次更新平衡因子+旋转的时间复杂度(O(1))
--------------------------------------------------------------------------------------------------------------------------
右单旋
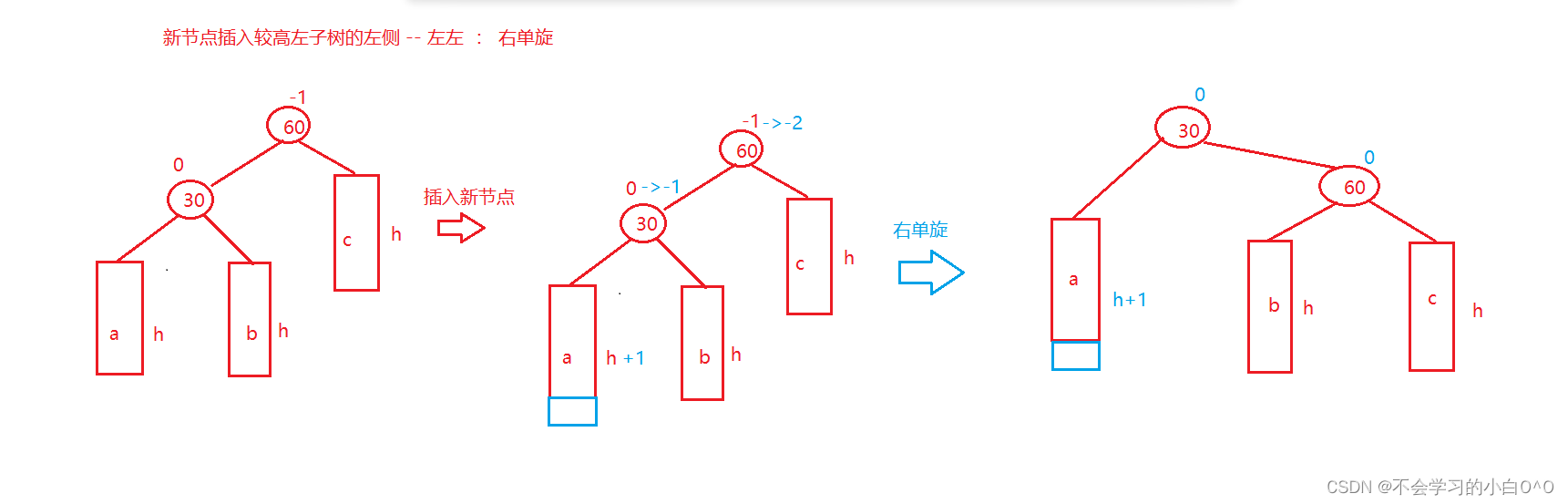
a、b、c是h大于等于0的平衡树